要点(最低100字)

目次

線形代数

  • 固有値・固有ベクトルの求め方
  • 固有値分解とは
  • 特異値・特位置ベクトルの概要
  • 特異値分解について

固有値・固有ベクトル

固有ベクトルは対応する行列をかけた際に、ベクトルの方向が変わらないベクトル。 固有値は固有ベクトルに行列をかけたときに何倍になるかを示す。

$$A\vec{a}=\lambda\vec{a} \tag{1}$$ のとき、$\vec{a}$が固有ベクトル、λが固有値

求め方は固有方程式で固有値を求めたあと、固有値を（１）式に代入して連立方程式を解く。

固有ベクトルの大きさについては１にしておくのが一般的。（※後の特異値を求めるときにそちらのほうが都合が良い）

固有値分解

固有値ベクトルを列ベクトルに持つ行列Vと、対応する固有値を対角成分に持つ対角行列Λを用いて行列Aは以下の式に分解できる。

$$ A = V\Lambda V^{-1} \tag{2}$$

プログラミング的には、対角行列の演算負荷が低いことから、計算速度向上、リソース節約につながる。

import numpy as np
values,vectors = np.linalg.eig(matrix)

特異値・特異ベクトル

固有値については正方行列のみしか扱えなかったが、これをm×nの行列に拡張したもの。

Uの列ベクトルを左特異ベクトル、、Vの列ベクトルを右特異ベクトルという。 Σの対角成分は特異値という。 ※このとき、ベクトルのノルムは１、σ>0,特異値の数はmin(m,n)となる。今回はｍ＜ｎとした。

$$ A = U\Sigma V^{\top} \tag{3}$$

$$A\vec{v}=\sigma\vec{u} \tag{4}$$

$$A^\top\vec{u}=\sigma\vec{v} \tag{5}$$ $\sum =$ $$ \begin{pmatrix} \sigma_{1} & 0 & \dots & & &0 \ 0&\sigma_{2}& 0 & \dots & &0\ 0 & 0 &\ddots&0 &\dots&\vdots\ \vdots&\dots&0&\sigma_m&0&\dots \end{pmatrix} $$

特異値分解

  1. $AA^\top$または$A^\top A$を求める　（計算量の問題で、$A^\top A$のほうが次数が少ないときはそちらを使う。式(4)に$A^\top$を掛けるか、式(5)にAを掛けるかの違い）
  2. $AA^\top$または$A^\top A$の固有方程式を解く
  3. 固有値の正の平方根を特異値とする
  4. 特異値を$(A^{\top} A - \sigma^2 E) \vec{v} = \vec{0}$または$(AA^{\top} - \sigma^2 E ) \vec{u} = \vec{0}$に代入して、どちらかの特異ベクトルを求める※重解のときはグラムシュミットの直交化方を用いて、同じ特異値に対する特異ベクトルを直交化すること。
  5. 式(4)または(5)を用いてもう一方の特異ベクトルを求める
import numpy as np
u,sigma,vt = np.linalg.svd(matrix)

確率・統計

  • 条件付き確率について理解を深める
  • ベイズ則の概要を知る
  • 期待値・分散の求め方
  • 様々な確率分布の概要を知る

客観確率と主観確率

  • 客観確率：頻度確率とも言う。データに基づく事実
  • 主観確率：ベイズ確率。条件の元で推測される信念の度合い。　診断など

条件付き確率

事象Y＝ｙが与えられた上での、事象X=xとなる確率 $P(X=x|Y=y) = \frac{P(X=x,Y=y)}{P(Y=y)}$

同時確率

事象X＝ｘ∧事象Y=yとなる確率 2つ目はXとYを入れ替えても同じ。　※実運用上はyが観測変数でxが直接観測出来ない変数になる 2つ目の式がベイズ則に繋がる。

$$P(X=x,Y=y) =\ \begin{cases} P(X=x) \times P(Y=y) &(XとYが独立) \ P(X=x|Y=y) \times P(Y=y)&(XとYが独立でない) \end{cases} $$

期待値と分散

  • 期待値　$E(X) = \int P(X)f(X)dx$ 離散変数ならΣ
  • 分散　$E(f(X)^2)-(E(f(X)))^2$
  • 共分散　$E(fg(X)) - E(f)E(g)$

主要な確率分布

  • ベルヌーイ分布　
    • 説明：2種類の結果のみが得られるベルヌーイ施行の結果を示す確率分布
    • 式：$P(x|\mu) = \mu^x(1-\mu)^{(1-x)}$ μはxが真の確率、xが真のときx=1,偽のときx=0
    • 期待値：p
    • 分散: p(1-p)
  • 二項分布
    • 説明：ベルヌーイ施行を繰り返し行ったときのその成功回数の分布
    • 式：$P(x|\lambda,n) = _nC_x \times \lambda ^x(1-\lambda)^{(1-x)}$ λは成功確率、xは成功回数,ｎは施行回数
  • 正規分布
    • 説明:
    • 式$X(x;\mu,\sigma^2) = \sqrt{\frac{1}{2\pi\sigma^2}} \times \exp(-\frac{(x-\mu)^2}{2\sigma^2})$

情報理論

  • 自己情報量・シャノンエントロピーの定義
  • KLダイバージェンス・交差エントロピーの概要 /img/Pasted_image_20230705165144.png

自己情報量

$I(x) = -log(P(x))$

底によって単位を変える。

  • 2:bit
  • e:nat

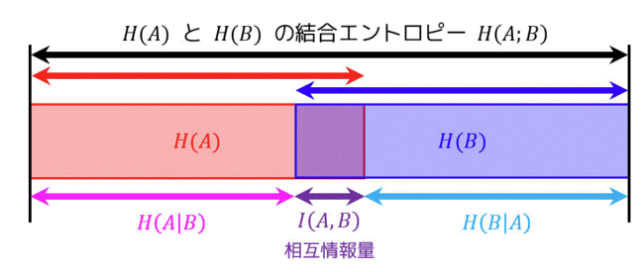
シャノンエントロピー

各事象の情報量の平均 自己情報量の期待値 $H(x) = - \sum P(x) \times log(P(x))$

KLダイバージェンス

2つの確率分布の類似度合いを見る指標。０に近いほど分布が近く、大きくなるほど分布が異なる。 KL情報量ともいう。 PとQについて非対称。

$D_{KL}(P||Q) = \int_{-\infty}^{\infty}p(x) \log \frac{p(x)}{q(x)}dx$

p(x)側にデータサンプルから得られた確率。q(x)側に想定する確率分布を取ることで、想定分布がどの程度データの特徴を捉えているかを評価できる。

VAEなどで潜在変数の分布のパラメータをKLダイバージェンスを損失関数に取ることで学習できる。

ギブスの不等式により、 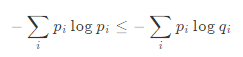/img/Pasted_image_20230125204336.png なので、必ず非負の値になる。

交差エントロピー

KLダイバージェンスの対数の分母側を切り出した値。 Qの自己情報量をPの分布で平均する。

$H(P,Q) = H(P) + D_{KL}(P||Q)$

実装演習結果

今回は実装なし。

考察

数学の内容なので特に考察ではないが、 今回受けたステージテストのように選択肢問題であることを考えると、 愚直に解かなくても選択肢から確認する必要のある項目だけチェックすれば解答速度を上げられるように感じた。

参考文献/サイト

固有値分解 | 行列の分解 | プログラマーのための線形代数 工業大学生ももやまのうさぎ塾