DeepLearningDay1
要点(最低100字)
識別と生成
- 識別：データを目的別クラスに分類する
- $P(C_k|x)$：条件Xが与えられた条件の元でのクラスkの確率
- 高次元から低次元へ
- 必要な学習データは比較的少ない
- 応用例
- 画像認識
- 生成：特定クラスのデータを生成する
- $P(x|C_k)$：クラスｋという条件のものとでのデータCkの分布
- 低次元から高次元へ
- 必要な学習データが多い
- 応用例
- 画像の超解像
- テキスト生成
主要なモデル
- 識別モデル
- 決定木
- ロジスティック回帰
- SVM
- ニューラルネットワーク
- 生成モデル
- 隠れマルコフモデル
- ベイジアンネットワーク
- VAE
- GAN
- DRAW
識別器の開発アプローチ
上から順に学習コストが大→小
- 生成モデル的アプローチ
- ベイズの定理を活用
- モデル化の対象
- 各クラスの生起確率
- データのクラス条件付き密度
- モデル化の対象
- データを人工的に生成できる
- 確率的な識別
- ベイズの定理を活用
- 識別モデル
- 決定理論に基づき識別結果を得る
- データがクラスに属する確率をモデル化
- 確率的な識別
- 識別関数
- 入力値ｘを直接クラスに写像（変換）する関数f(x)を推定
- データの属するクラス情報のみ（確率は計算されない）
- 決定的な識別
生成モデルと識別モデルの比較
生成モデルのアプローチではより複雑なデータ分布を学習しようとするので、計算量が多い。
（講義ビデオより引用）
識別モデルと識別関数
モデルは推論結果の取り扱いを変更でき、間違いの程度も評価できるが 識別関数ではそれらが出来ない。結果を一足飛びに得る。
（講義ビデオより引用）
深層学習の強み：万能近似定理
万能近似定理：活性化関数をもつネットワークを使うことで、どんな関数でも近似できるという定理 これまでの機械学習では人間が関数を設計していた ノーフリーランチの定理
ニューラルネットの数学的表現
(ラビットチャレンジの深層学習day1講義資料より引用)
回帰と分類の違い
回帰：連続する実数値を取る関数の近似 分類：離散的な結果を予想するための分析
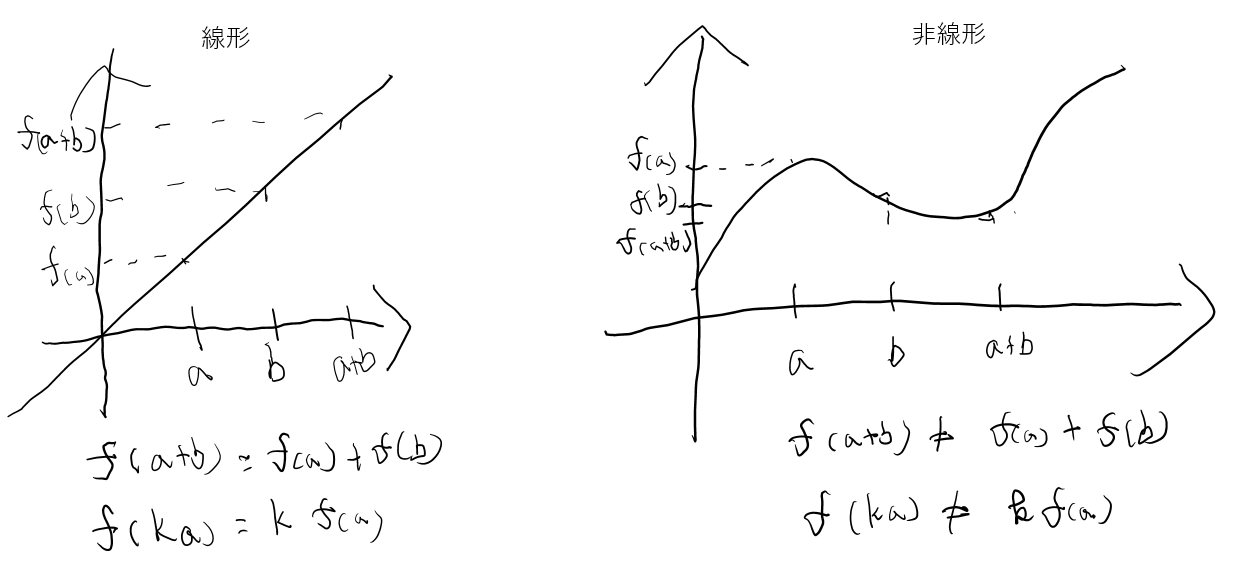
線形と非線形の違い
線形な関数は以下の性質を持つが、非線形関数は持たない。
- 加法性:$f(a+b) = f(a) + f(b)$
- 斉次性$f(ka) = k\times f(a)$
活性化関数
ステップ関数
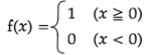
def step_func(x):
if x > 0:
return 1
else:
return 0
問題点：線形分離可能なものしか学習出来なかった
シグモイド関数
def sigmoid_func(x):
return 1/(1+np.exp(-x))
問題点：勾配消失問題
ReLU関数
def relu_func(x):
return x if (x>0) else 0
勾配消失問題とスパース化に貢献
誤差関数
回帰問題に使う誤差関数
MSE：$E_n(w) = \frac{1}{2} \sum_{j=1}^{J} (y_j - d_j)^2 = \frac{1}{2} ||(y - d)||^2$
分類に使う誤差関数
Cross Entropy Error：$-\sum_{i=1}^I d_i log(y_i)$
パラメータ更新手法
勾配降下法
ηを学習率として、以下のようにパラメータ更新を実施する。
$$w^{(k+1)} = w^{(k)} - \eta \frac{\partial E(w)}{\partial w}$$
特徴
- 全サンプルの誤差を用いるので、効率が悪い
- 学習率の大きさによって学習の収束性や効率が大きく異なる
- 学習率が大きすぎる：収束しない
- 小さすぎる：収束までに時間がかかる。局所解に陥る可能性がある
参考：学習率についてはAdamなどの収束性向上のためのアルゴリズムが存在する（Day2）
確率的勾配降下法
ランダムに抽出したサンプルの誤差でパラメータ更新を行う。
$$w^{(k+1)} = w^{(k)} - \eta \frac{\partial E_i(w)}{\partial w}$$
特徴
- データが冗長な場合の計算コストの削減
- 望まない局所最適解に陥る可能性の低減
- オンライン学習ができる
ミニバッチ勾配降下法
ランダムに分割したデータ集合（ミニバッチ）Dtに属するサンプルの平均誤差でパラメータ更新を行う。
$$
\begin{split}
&w^{(t + 1)} = w^{(t)} - \epsilon \nabla E_t \
&E_t = \frac{1}{N_t} \sum_{n \in D_t} E_n \
&N_t = | D_t | \ & (N_t: バッチ数)
\end{split}
$$
特徴
- 確率的勾配降下法のメリットを損なわず、計算機の計算資源を有効活用できる
- CPUのスレッド並列化
- GPUのSIMD(Single Instruction Multi Data)並列化
勾配の計算法
数値微分
数学の微分の定義に従って、微小に値をずらしたときの値を用いて計算する。 $\frac{\partial E}{\partial w_m} \approx \frac{E(w_m + h) - E(w_m - h)}{2h}$
問題点：順伝播の計算回数が増えるため、負荷が大きい
誤差逆伝播
算出された誤差を、出力層側から順に微分し、前の層前の層へと伝播。（チェインルール） 最小限の計算で各パラメータでの微分値を解析的に計算する手法
(講義スライドより引用)
メリット：誤差（計算結果）から微分を逆算していくことで、不要な再帰的計算を避けて微分を算出できる
MSEの例
$$\Rightarrow
\frac{\partial E}{\partial w_{ji}^{(2)}}
= \frac{\partial E}{\partial y} \frac{\partial y}{\partial u} \frac{\partial u}{\partial w_{ji}^{(2)}} = (y - d) \cdot 1 \cdot
\left[
\begin{array}{c}
0 \
\vdots \
z_i \
\vdots \
0
\end{array}
\right]
= (y_j - d_j) z_i$$
モデルの設計
入力層
取りうるデータ
- 連続実数
- 確率
- フラグ値
取るべきでないデータ
- データの質に関する観点
- 欠損値が大きいデータ
- 誤差の大きいデータ
- モデルの分離に関する観点
- 出力そのもの、出力を加工した情報（人間の変換部分とはしっかり分離すること）
- 値の尺度に関する観点（線形変換を挟んでいる以上、あまりに値間の関係性が無いとうまくいかない）
- 連続性の無いデータ
- 無意味な値が割り当てられているデータ
前処理
- 欠損値処理：零埋め、除外
- データの結合
- 数値の正規化・標準化
データ拡張 Data Augumentation
学習データが不足するときに、人工的にデータを作り水増しする手法 分類タスクに効果が高い
<入力データの加工例>
（講義より引用） ）
※中間層にノイズを入れることで、様々な抽象化レベルでのデータ拡張が可能
注意点
- 現実にあり得る変換をすること
- ラベルと一致しなくなるような処理をしない（６のラベルのついた画像を180度回転させるなど）
- ランダムにデータ拡張を行う際には学習データの違いからくる再現性の問題に注意
- モデルの性能とデータ拡張の効果の分離
- ノイズ付加などの一般的に適用可能なデータ拡張はドロップアウトのようなモデルの一部とみなす
- クロップなどの特定のタスクに対してのみ有効なデータ拡張は入力データの事前拡張とみなす （例：）
過学習
訓練データに過度に適合して、汎化性能の低いモデルになること。 パラメータ数の多いNNで発生しやすい（モデルの表現力の高いとき）
見分け方：テストデータの誤差が小さくならない 予防策：ドロップアウト、アーリーストッピング
<過学習と誤差>
＜ドロップアウト＞
（講義スライドより引用）
開発環境について
- デバイスの種類
- CPU
- GPU
- FPGA：自分でプログラムできる計算機で特定用途で高速
- ASIC：プログラム×計算機。Googleのテンソル処理に最適化されたTPUが有名
- クラウドサービス
- AWS
- GCP
講義中の課題
- 確認１
- ディープラーニングは何をしようとしているか？ 複数の隠れ層による入力から目的とする出力への変換を行うモデルを構築すること。
- 最適化の対象は？ ③重みと④バイアス
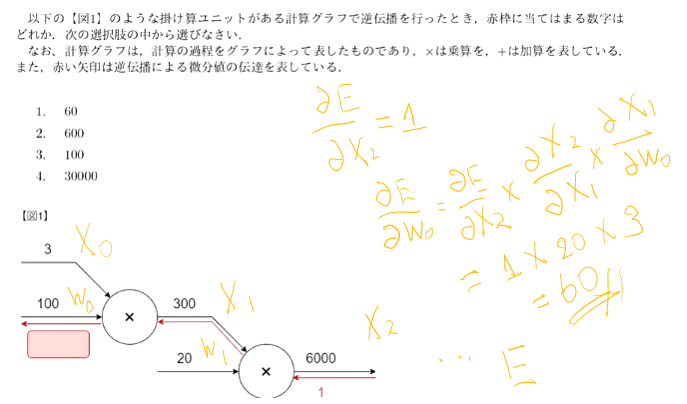
- 確認２：入力２ノード、中間層３ノード２層、出力１ノードのニューラルネットをかけ。
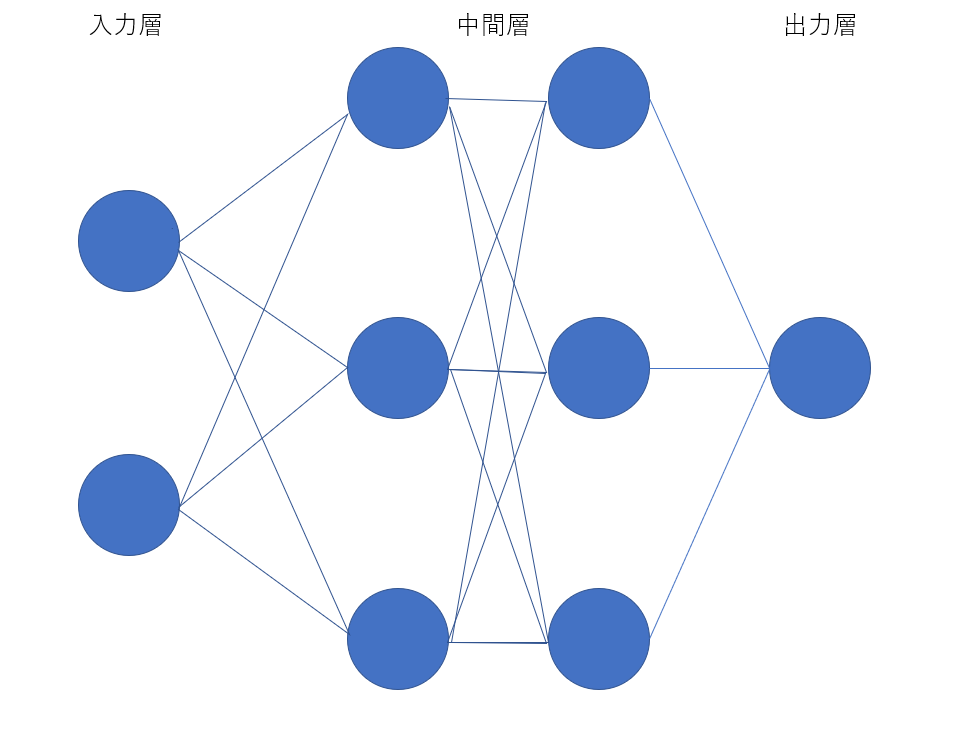
- 確認３：動物分類ネットワークの例をかけ
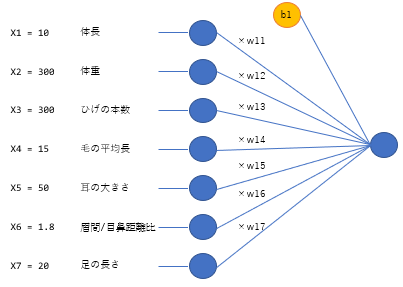
- 確認４：$u = WX+b$の計算をpythonでかけ
import numpy as np u = np.dot(W,X) + b
- 確認５：1-1のファイルから中間層の出力を定義しているソースを抜き出せ
```python
# 2層の総入力
u2 = np.dot(z1, W2) + b2
# 2層の総出力
z2 = functions.relu(u2)
- 確認６：線形と非線形の違いを図に書いて簡単に説明せよ
- 確認７：活性化関数に該当する箇所をぬきだせ
# 1層の総出力 z1 = functions.relu(u1)
# 2層の総出力
z2 = functions.relu(u2)
- 確認８：$E_n(w) = \frac{1}{2} \sum_{j=1}^{J} (y_j - d_j)^2 = \frac{1}{2} ||(y - d)||^2$について２乗する意味と1/2する意味は？
ただ引き算する場合だと、誤差に対して符号がついてしまい、y-dが負のときに誤差があるのに良いモデルとして学習してしまうから。
1/2は単純に2乗の値を微分したときにでてくる2倍の操作と打ち消して計算を簡単にする便宜的な意味がある。
- 確認9:（１）～（３）に該当するソースコードを抜き出し、各行に説明を記載せよ
$\overbrace{f(i, u)}^{(1)} = \frac{\overbrace{e^{u_i}}^{(2)} }{ \underbrace{\sum_{k=1}^{K} e^{u_k}}_{(3)} }$
```Python
def softmax(x):
if x.ndim == 2:
# ミニバッチのときの処理
x = x.T # 転置
x = x - np.max(x, axis=0) # オーバーフロー対策
y = np.exp(x) / np.sum(np.exp(x), axis=0) # ソフトマックスの計算 各クラス確率の合計が１になるようにスケーリング
rerurn y.T # 転置
x = x - np.max(x) # オーバーフロー対策
return np.exp(x) / np.sum(np.exp(x)) # ソフトマックスの計算
```
- 確認10：(1)～(2)の数式に該当するソースコードを示し、1行ずつ処理の説明をせよ。$\overbrace{E_n(w)}^{(1)} = \overbrace{- \sum_{i=1}^{I} d_i \log y_i}^{(2)}$
```python
def cross_entropy_error(d, y):
if y.ndim == 1: # 1次元行列の場合
d = d.reshape(1, d.size) # 2次元行列に変形
y = y.reshape(1, y.size) # 2次元行列に変形
if d.size == y.size:# 教師データｄがone-hot-vectorの場合
d = d.argmax(axis=1) # 正解クラスのインデックスを取得
batch_size = y.shape[0] # バッチサイズを取得
return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7)) / batch_size # 交差エントロピーを計算して返す ＋1e-7はx→0でlog(x)→-∞になることの対策。数式中のdiは正解クラスのとき１でそれ以外が0なので、バッチ内の各要素についてはモデルが予測した正解クラスの確率の対数の逆符号を取れば良い。バッチ方向に和を取っているので、最後にバッチサイズで割っている
-
確認１１：オンライン学習とはなにか？ 学習データが入ってくるたびにパラメータ更新を行う方法。もう一方のバッチ学習はすべてのデータを用いて一度にパラメータ更新を行う。
-
確認１２：$w^{(t + 1)} = w^{(t)} - \epsilon \nabla E_t$の意味を図で説明せよ ※ｔはエポックの番号
-
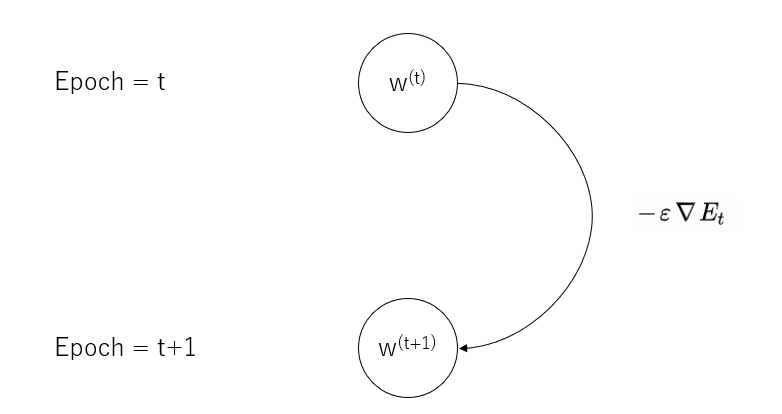
確認１３：誤差逆伝播法では不要な再帰的処理を避ける事が出来る。 既に行った計算結果を保持しているソースコードを抽出せよ。
# 出力層でのデルタ delta2 = functions.d_mean_squared_error(d, y) # b2の勾配 grad['b2'] = np.sum(delta2, axis=0) # W2の勾配 grad['W2'] = np.dot(z1.T, delta2) # 中間層でのデルタ #delta1 = np.dot(delta2, W2.T) * functions.d_relu(z1) ## 試してみよう delta1 = np.dot(delta2, W2.T) * functions.d_sigmoid(z1) delta1 = delta1[np.newaxis, :] # b1の勾配 grad['b1'] = np.sum(delta1, axis=0) x = x[np.newaxis, :] # W1の勾配 grad['W1'] = np.dot(x.T, delta1)
```
問題１：チェインルールにしたがって計算をしていけば良い。
問題２：ベイズの定理で計算する
実装演習結果
1_1_forward_propagation.ipynb
順伝播（単層・単ユニット）
順伝播（単層・複数ユニット）
順伝播（3層・複数ユニット）
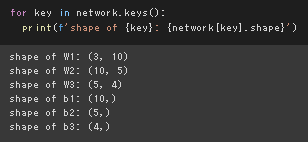
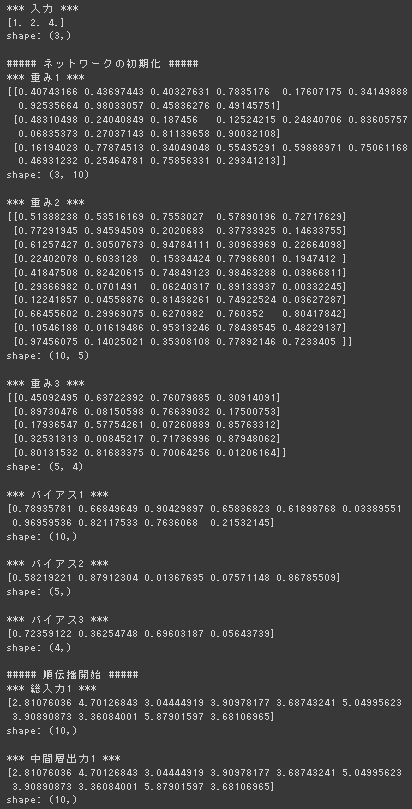試してみよう１：形状の出力
試してみよう２：ネットワークの初期値のランダム生成
重みはもともとランダム生成だったので、隠れ層のノード数などをランダム生成した。
多クラス分類（2-3-4ネットワーク）
デフォルト実行 （コードが2-3-4になってなかったので修正して実行）
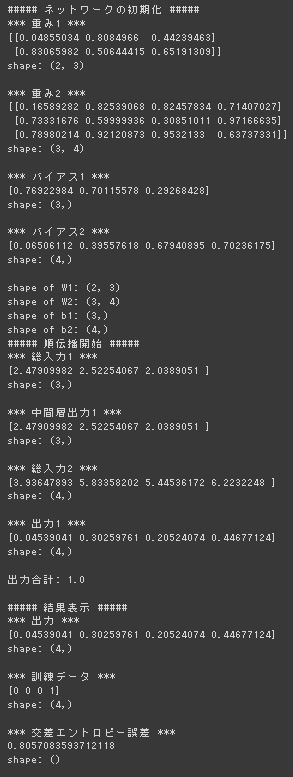3-5-6に変更して実行
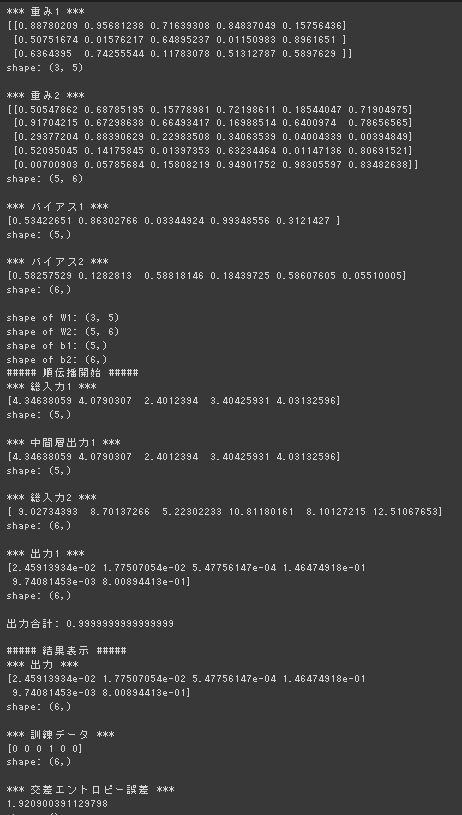
回帰（2-3-2ネットワーク）
3-5-4のネットワークに変更して実行
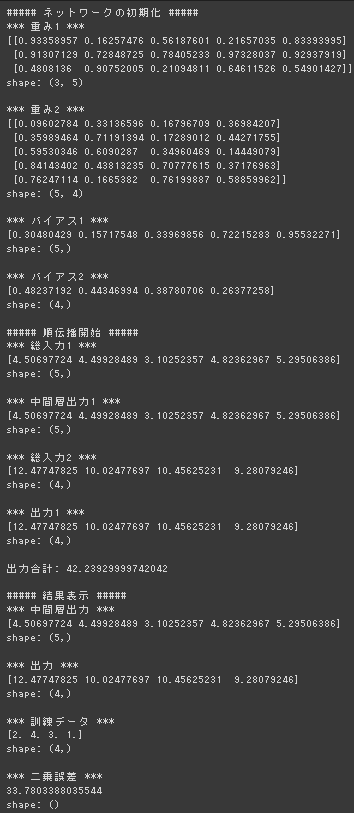
2値分類（2-3-1ネットワーク）
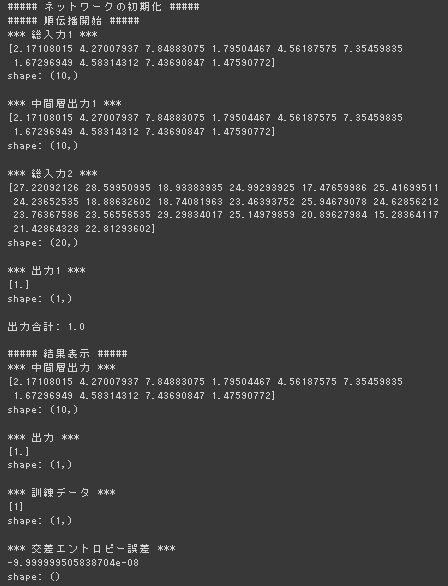
1_3_stochastic_gradient_descent.ipynb
確率勾配降下法
デフォルトの結果(ReLU、※誤差逆伝播のデルタがシグモイドになっていたため修正)
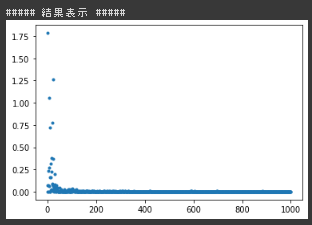
シグモイドの結果(入力0~1)
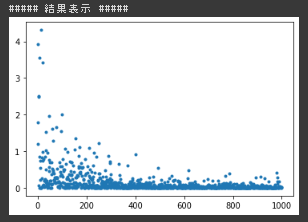シグモイドの結果（入力0~10）
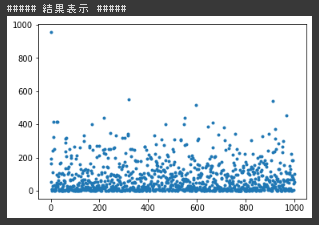シグモイドの結果（入力-5~5）
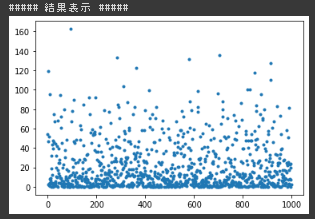
考察
確率的勾配降下法の実装演習において ReLU+入力の初期値-5~5 だと勾配爆発で学習がうまくいかなかった。 重みの初期化が正の値の範囲なので、目標出力が入力の線形結合であることを考えると負値を一様に０にするReLUとの相性が良くなかったと考えられる。 実際、初期値の値を正の値の範囲にずらした場合は学習が進んだ。
Sigmoidを使ったケースにおいては入力値のスケールによって結果にかなりのばらつきが見られた。 Sigmoid関数自体が入力の値域を0~1にまるめてしまうので、 今回のケースの様に入力の線形結合を目的関数とするような入力値のスケールを維持したほうが良いケースでSigmoid関数を使うのは適切でないのではないかと考えた。