要点(最低100字)

勾配消失問題

誤差逆伝播の復習

誤差から微分を逆算していくことで不要な再帰的計算を避けて微分を算出できる

確認問題１

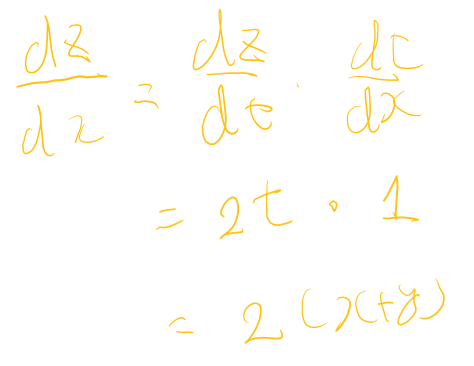
勾配消失問題の復習

誤差逆伝播が入力層に進んでいくに連れて勾配がどんどん減衰していくために パラメータ更新が入力層に近い側で進まなくなり、最適値に収束しなくなる現象

微分値の絶対値が１未満になると減衰していくことになる。

活性化関数の微分

$(1-sigmoid(x))\cdot sigmoid(x)$ シグモイド関数の微分は最大値が0.25であり、多層になると減衰が進んでいく。 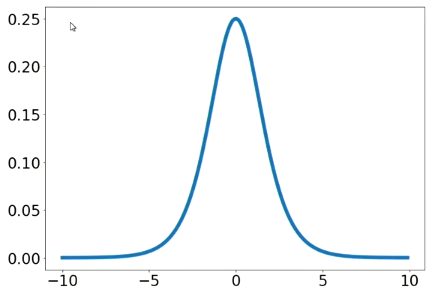（実装ノートより引用）

確認問題２

（２）

活性化関数による勾配消失対策

ReLU関数：勾配消失問題への対応とスパース化で貢献

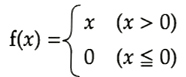（講義スライドより引用） 微分値は正の範囲で１，負の範囲で０

重みの初期化

Xavierの初期化

手法

正規分布での初期化値を一つ前の層のノード数で割る。（初期の方法でLeCunが提案したもの。） →各レイヤの出力の分散は「$n_{in} \times var_{in} \times var_{out}$」となるので、出力の分散を入力ノード数で割ることで分散を一定にできる。 逆伝播の方向も考慮した、入出力の平均値で割ってスケーリングするのが現在の方法

network['W1'] = np.random.randn(input_layer_size, hidden_layer_size) / np.sqrt((input_layer_size+hidden_layer_size)/2)
network['W2'] = np.random.randn(hidden_layer_size, output_layer_size) / np.sqrt((hidden_layer_size+output_layer_size)/2)

対象の活性化関数

• sigmoid
• 双曲線関数 ※Xavierの初期化は0近辺で線形近似できる前提をおいているので、ReLUには使えない。

効果

もともとSigmoidに対して、正規分布で初期化した際は活性化関数への入力が０から外れすぎることで出力が0か1に偏っていたのが、 分散を抑制することで0~1にうまくバラける様になった。

またネットワーク全体で見たときに各層の分散が一定に保たれる。

Heの初期化

手法

あるレイヤーを経た後の出力の分散は、ReLU を考慮すると、「1/2 × $n_{in}$ × 入力の分散 × 重みの分散」となります。そこで、Kaiming (He) 初期化では、重みを

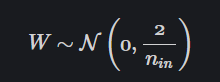
として、標準偏差が $\sqrt{2/n_{in}}$ の正規分布によって初期化

network['W1'] = np.random.randn(input_layer_size, hidden_layer_size) / np.sqrt(input_layer_size) * sqrt(2)
network['W2'] = np.random.randn(hidden_layer_size, output_layer_size) / np.sqrt(hidden_layer_size) * sqrt(2)

対象の活性化関数

• ReLU

効果

ReLUに対して正規分布で初期化すると出力がほぼ０になるため表現力が失われていた。（活性化関数の式を見ればわかる） Heの初期化をすることによって出力分布が0~1にうまくバラける。

確認問題３

各層の出力がバイアスのみの関数になるといえるため、 入力に関係の無い、出力値の平均を学習するだけになる。

バッチ正規化

ミニバッチ単位で入力値の偏りをなくす手法。 活性化関数の前にバッチ正規化の処理を加える。 (各層の入力 OR 線形変換後の値）

処理

1. ミニバッチ単位での平均を求める
2. ミニバッチ単位での分散を求める
3. 求めた平均と分散によって標準化
4. 標準化した値をスケーリング及びシフトさせる （Neural Nets and Optimization Algorithms (Fully Connected and Convolutional Neural Nets) – Yogesh Luthra – Machine Learning, Data Science, Artificial Intelligence, Statisticsより引用） ※θはゼロ除算などを避けるための運用上の微小値

効果

• 学習の高速化：極端に小さい値をクリッピングすることによる勾配消失問題への対応
• 学習の安定化：アクティベーション前後の分布が変化してしまう内部共変量シフトへの対応
• 過学習への対応：各層で正規化処理を行うことになるので外れ値が減り、過学習が抑制される。

確認問題４

内部共変量と勾配消失問題への対応

例題チャレンジ

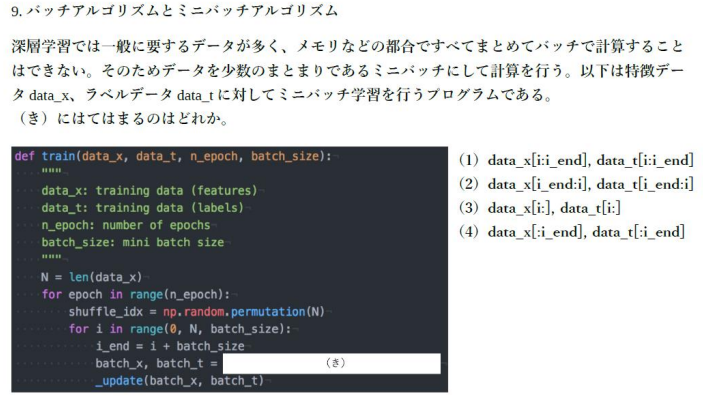（講義スライドより引用） 回答：（１）

学習率最適化手法

はじめに

勾配降下法によってパラメータを最適化していくが その際に学習率の取り扱いが重要になる。 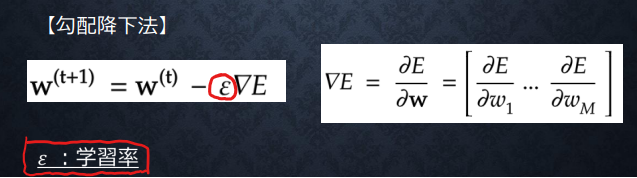（講義スライドより引用）

学習率のトレードオフ

• 大きいと最適値にたどり着かずに発散
• 小さいと
  • 収束までに時間がかかる
  • 局所最適解に陥る

学習率の最適化

• 学習の段階に応じて学習率の大きさを小さくしていく
• パラメータごとに可変にしていく

主な学習率最適化手法

• モメンタム：前回の更新量に係数をかけたものを更新に使う
• AdaGrad：パラメータの要素ごとに学習率を調整する。勾配の絶対値が大きい要素には更新量を小さくする
• RMSProp：
• Adam

※勾配に対する挙動についてはGitHub - Jaewan-Yun/optimizer-visualization: Visualize Tensorflow’s optimizers.を参考にすると良い

モメンタム

※学習率自体の調整ではない $V_t = \mu V_{t-1} - \epsilon \nabla E$ $W^{(t+1)} = W^{(t)} + V_t$

メリット

• 局所最適解に陥りにくい
• 最適値への収束が早い

AdaGrad

$h_0 = \kappa$　　　　　　　　　　　 ：任意の値で初期化 $h_t = h_{t-1} + (\nabla E)^2$　　　　　　 ：勾配の二乗の値を累積していく $W^{(t+1)} = W^{(t)} - \epsilon \frac{1}{\sqrt{h_t}+\theta} \nabla E$ 　　：ｈを用いて学習率を減衰させていく ※θは調整項、学習率の減衰が常に入っていくので初期値は他の方法の１０倍程度にしておく

メリット

• 誤差への影響が稀な特徴量に対する感度があがる

デメリット

• 誤差が減るにつれ学習率が小さくなっていくので鞍点問題を起こしやすい
• 勾配が急なところで最適解にたどり着けないことがある

RMSProp

AdaGradの改良版 $h_0 = \kappa$　　　　　　　　　　　 ：任意の値で初期化 $h_t = \alpha h_{t-1} + (1-\alpha)(\nabla E)^2$　　 ：勾配の二乗の値について過去の値と今回の値で移動平均をとる $W^{(t+1)} = W^{(t)} - \epsilon \frac{1}{\sqrt{h_t}+\theta} \nabla E$ 　　：ｈを用いて学習率を減衰させていく ※θは調整項

メリット

• 局所的最適解にはならず、大域的最適解となる
• ハイパーパラメータの調整が必要な場合が少ない

Adam

モメンタムとRMSPropの組み合わせ。 $V_t = \alpha V_{t-1} + (1-\alpha)(\nabla E)$ 　　：1次モーメント（勾配の移動平均） $h_t = \beta h_{t-1} + (1-\beta)(\nabla E)^2$ 　 ：2次モーメント（勾配の二乗の移動平均） $\hat{V_t}=\frac{V_t}{1-\alpha^t}$ 　　　　　　　　　 ：バイアス修正 $\hat{h_t}=\frac{h_t}{1-\beta^t}$　　　　　　　　　 ：バイアス修正 $W^{(t)} = W^{(t-1)} - \epsilon \frac{\hat{V_t}}{\sqrt{\hat{h_t}}+\theta}$

メリット

• 局所最適解に陥りにくい
• 最適値への収束が早い

確認問題５

モメンタムは過去の更新量を反映することで勾配が弱い領域でも学習が進むようになっているため収束が早く、局所最適解にも陥りにくい AdaGradは勾配の２乗の累積値で学習率を減衰させていくことで出現が稀な特徴量への感度を上げることができる RMSPropはAdaGradが学習段階初期の特徴量分布に大きく依存することを移動平均を取ることによって対応したもの。

過学習

特定の訓練データに特化して学習してしまうこと 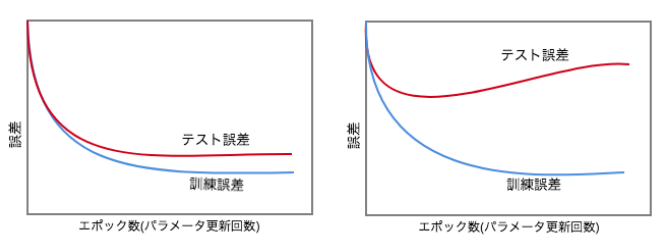（講義スライドより引用）

原因

ネットワークの自由度が高すぎること

• パラメータの数が多い
• パラメータの値域が適切でない
• ネットワークが深すぎる

対策

正則化を用いて自由度を制約する

確認テスト

（a）

正則化

過学習が起こらない範囲で重みのばらつきを出す必要がある。 重みに制約を与えることを荷重減衰という。WeightDecay

pノルムに係数をかけて誤差関数に加える。

$$\begin{array}{ll} E_n(w) + \frac{1}{p} \overbrace{\lambda}^{hyper \space parameter} || w ||_p^p & : 誤差関数に、pノルムのp乗を加える \
|| w ||_p = \Bigl( |w_1|^p + \cdots + |w_n|^p \Bigr)^{\frac{1}{p}} & : pノルムの計算 \end{array}$$ ※λの前の1/pは微分したときに無駄な係数が出ないための調整項。 P＝１のときマンハッタン距離 P＝２のときユークリッド距離 という

L1正則化

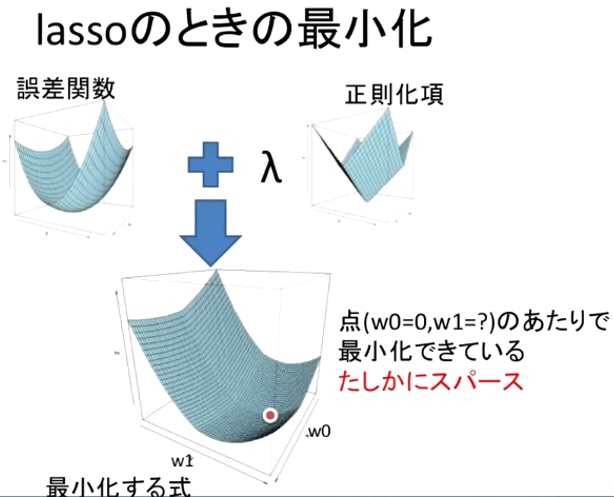（講義スライドより引用）

L2正則化

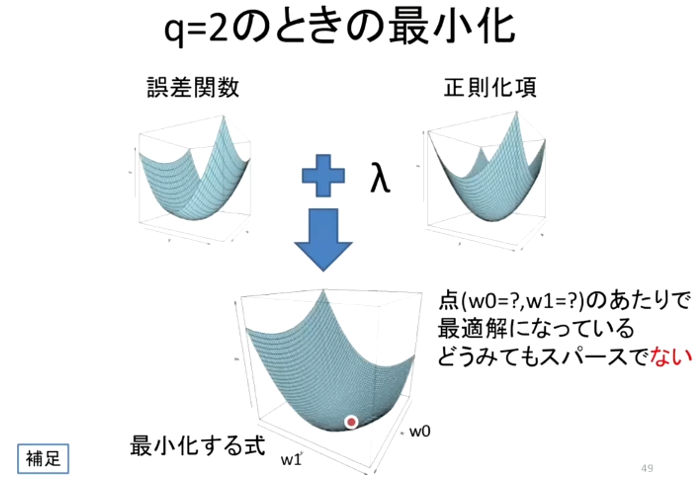（講義スライドより引用）

確認問題６

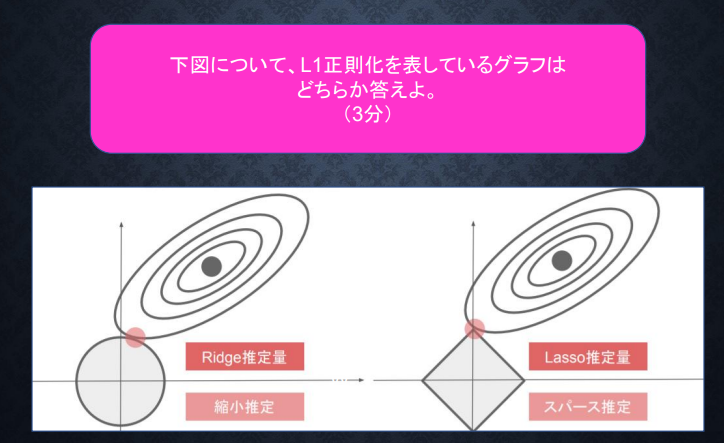右のLasso推定量、スパース推定のグラフ 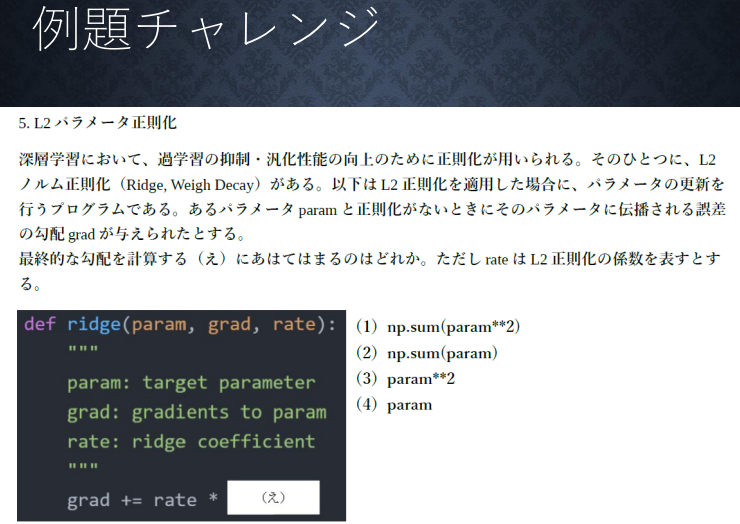（講義スライドより引用） 答え：（４） もとめたいのは微分結果で、損失関数に追加されている項は$\frac{1}{p}rate(||x||_p)^p$なので、paramのみがのこる 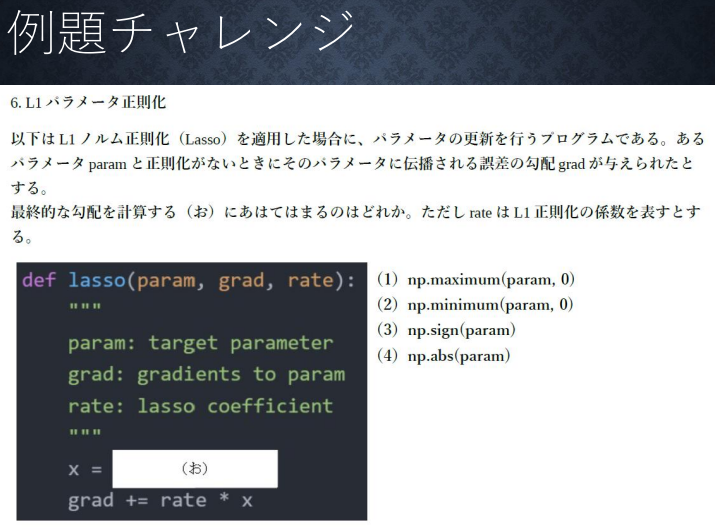答え：（３） 求めたいのは微分結果で、正則化項は1/1×rate×|w|なので、符号とrateが残れば良い。 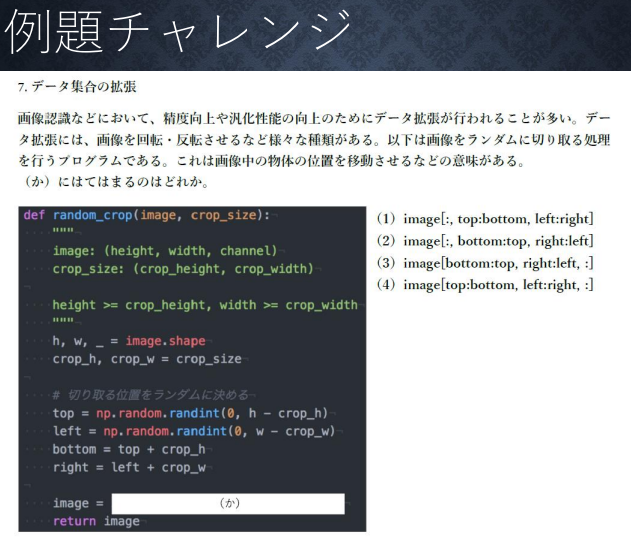答え：（４） 一般に画像データは左上が原点で今回のデータは関数の説明から縦→横→チャンネルの順だから。

ドロップアウト

学習時にランダムにノードを削除してパラメータを更新する。 推論時には落とさない。 ノード数が多すぎることによる過学習の対策。

複数の異なるモデルを学習するアンサンブル学習のような効果が得られる。

マルチタスク学習

複数のタスクを単一のモデルでまとめて解く手法

マルチタスク学習の仕組み

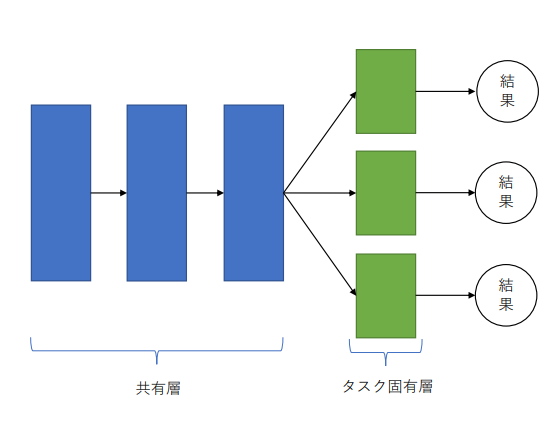（講義スライドより引用）

マルチタスク学習のメリット

• モデル数が少なくて済む
• タスクの相乗効果で個別のタスクの精度向上が期待できる
• 学習時間や総パラメータ数の削減

マルチタスク学習をする際の注意点

• 個別タスクで見たときには必要なメモリや演算量が増える
• 学習の難化

マルチタスク学習の例

画像から分類結果と物体検出を行う 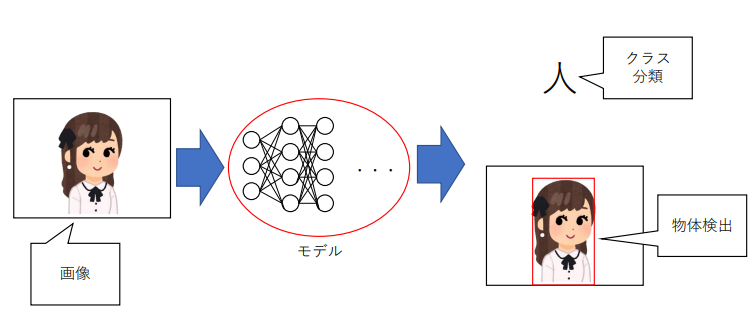（講義スライドより引用） 個別の文入力から穴埋めと文章推測を行う 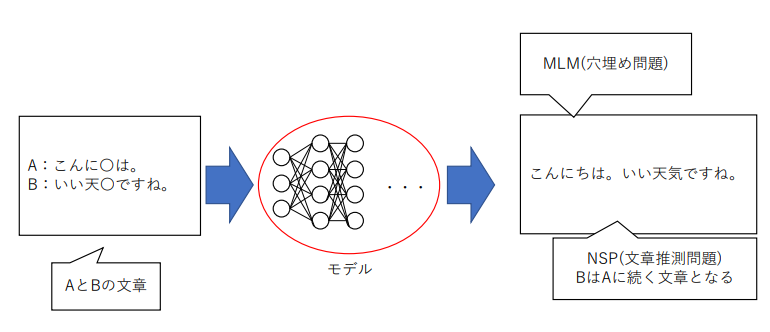（講義スライドより引用）

アンサンブル学習

バイアス：実測値と推測値の差 バリアンス：推測値のばらつき

過学習はバリアンスが高くてバイアスが低い状態といえる。

バイアスとバリアンスはトレードオフの関係にあり、うまくバランスを取ることが必要。

バギング

概要

全体から重複を許してランダムサンプリング(ブートストラップサンプリング )して それぞれのサンプルごとに個別のモデルを学習して

• 回帰なら平均値
• 分類なら多数決 の結果を全体の出力とする

主なモデルとしては ランダムフォレスト が上げられる 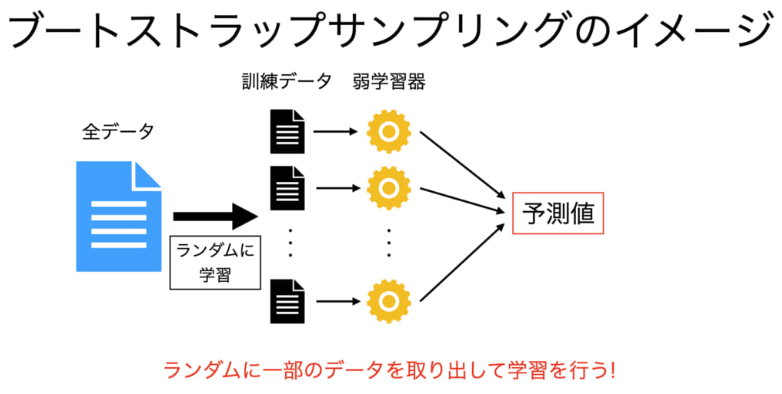(ブートストラップサンプリング – 【AI・機械学習用語集】より引用)

メリット

• 複数の弱学習器を使うことからバリアンスを抑えることができ、過学習を避けやすい
• 並列に処理できるため学習時間が短い

デメリット

• 精度向上自体はブートストラップサンプリングの多様性に依存するため思った程は無い
• (注意点)データのサンプリングをしすぎると結局バリアンスが高くなってしまい過学習に繋がる可能性がある

ブースティング

概要

バギングと異なりすべてのデータを利用する。 モデルの学習結果を受けてデータの重み付けを行い、 前のモデルの弱点を克服するモデルを順次学習して、 最終的に集計した結果を用いる。

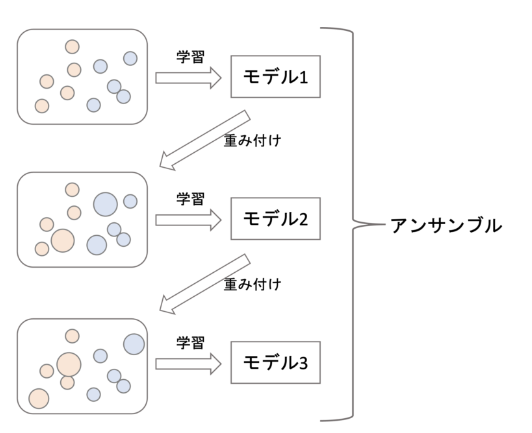(アンサンブル学習を超わかりやすく解説【機械学習入門30】より引用）

メリット

• モデルの弱点を克服するように学習していくのでバイアスが下がりやすい

デメリット

• 同じデータを何度も使うため、過学習に陥りやすい

スタッキング

概要

複数のモデルの結果を入力として学習するメタモデルを積み重ねていく手法 ２層より増やすこともある。 各モデルのバイアス、バリアンスのバランスを調整して最終的に高い精度を出すことができる。

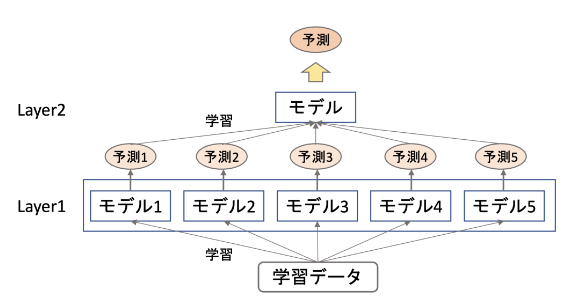
メリット

• 様々な計算方法を目的に合わせて使用できるため、精度が上がりやすい

デメリット

• 複数モデルを作り、その上でメタモデルも学習するので学習コストが大きい

畳み込みニューラルネットワークの概念

CNNの特徴として次元感で繋がりのあるデータを扱えるということがあげられる

LeNet

4層の畳み込みニューラルネットワークで画像特徴量を抽出し、 ２層の全結合層で抽出した特徴量によって文字の分類を学習する 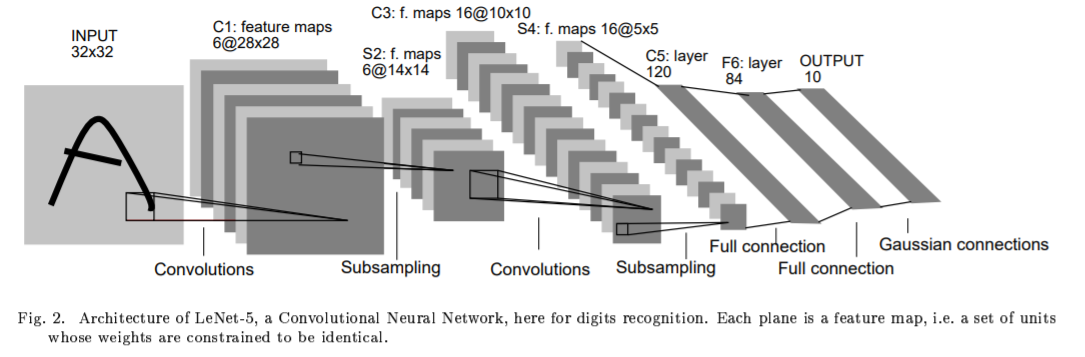(Yann LeCun et al. Gradient-Based Learning Applied to Document Recognitionより引用)

CNNの各処理の説明

確認問題６

回答：７×７ (6+1×2 - 2)/1 +1 = 7

初期のCNN

2012年のILSVRCにて他チームを圧倒する精度を出したネットワークモデル。 第三次AIブームの火付け役となった。

トロント大学ジェフリー・ヒントンが作成。

５層の畳み込み層と３層の全結合層。 過学習への対策に全結合層でのドロップアウトを使用している。

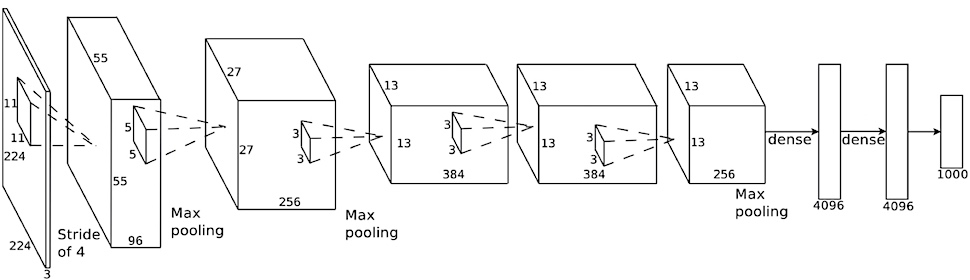(ImageNet Classification with Deep Convolutional Neural Networksより引用)

実装演習結果

2_1_network_modified.ipynb

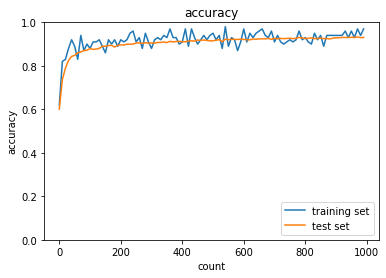
コードを一部変更して重みの初期化ごとの結果を確認した。

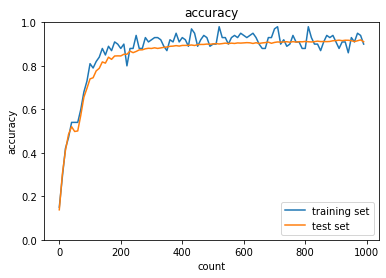
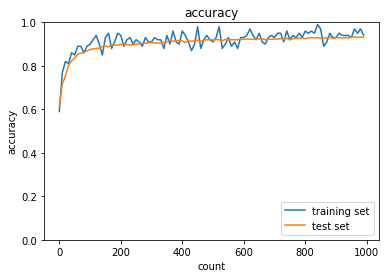
標準偏差0.01の正規分布	Xavierの初期化	Heの初期化	層ごとに変更
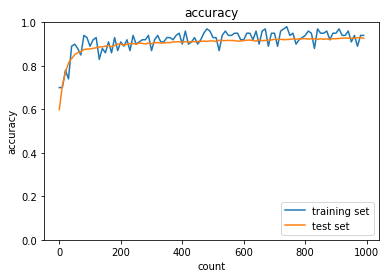実際に確認するには何度か実行して平均を取る必要があると思うが、重みの初期化を適切にしたほうが確かに学習初期から精度が上がる傾向があるように見受けられる。

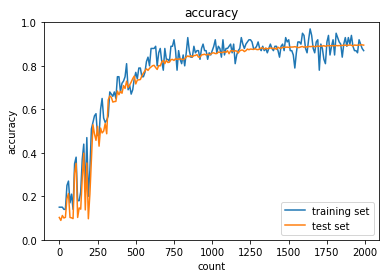
2_2_2_vanishing_gradient_modified.ipynb

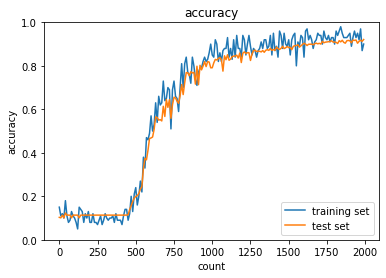
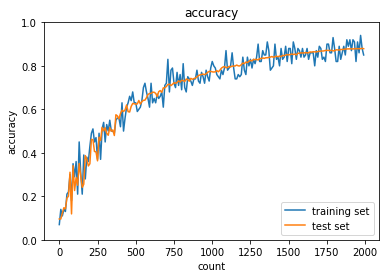
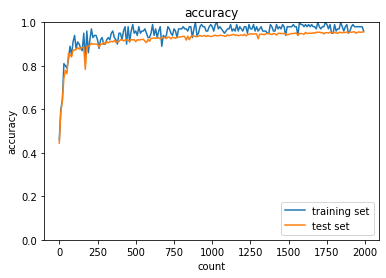
	sigmoid - gauss	ReLU - gauss	sigmoid - Xavier	ReLU - He
（40,20）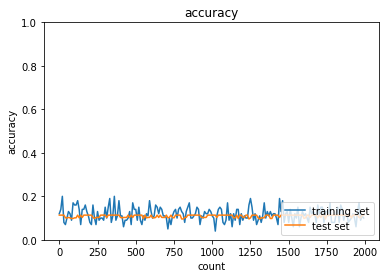
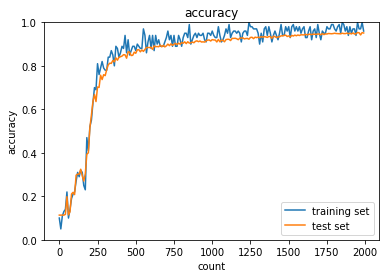
（400,200）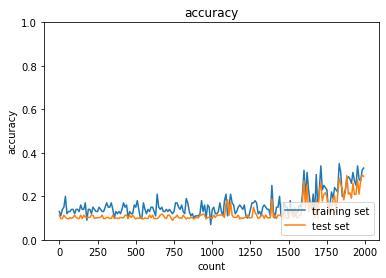
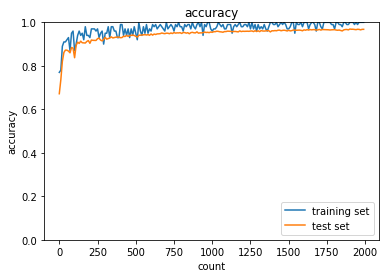Sigmoid-gaussの組み合わせは想定どおり、初期分布によって微分値が０に近い領域に入る傾向が出てしまいやはり学習がすすまなかった。
ReLU-GaussはSigmoidよりはマシなものの、初期値によってReLUへの入力が負になったときに誤差逆伝播の値が０になってしまうため適切なスケーリングで深い負の値への分布を抑えないと学習が進みづらいように見える。
Sigmoid-Xavierの組み合わせはスケーリングによって学習が進む様になっているが、Sigmoid自体の勾配が入力層に近づくにつれて減衰する傾向は変わらないので、学習に時間がかかっている
ReLU-Heについては初期値で学習初期から学習が進みやすくなっており、勾配が減衰する傾向もないので、スムーズに学習が進んでいる様に思われる。

try： hidden_size_listの数字を変更してみよう

Gaussのケースで設定しているハイパーパラメータが各種初期化方法と近くなれば学習の進み方は改善され、隠れ層のノード数を増やしているので表現力が上がって精度は若干良くなっている。 XavierやHeはそもそも入出力の分散が変わらないようにしているので、ノード数変更による表現力の違いの影響だと思われる。 モデルの表現力自体はデフォルトの隠れ層でReLU-Heの組み合わせを見る限り十分に見受けられるので、改善効果は初期値の分布のスケーリングが改善されたかどうかが大きいかと思われる。

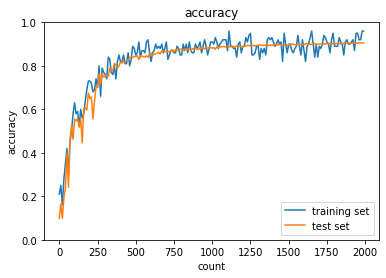
try :sigmoid - He と relu - Xavier についても試してみよう

sigmoid - He	ReLU - Xavier

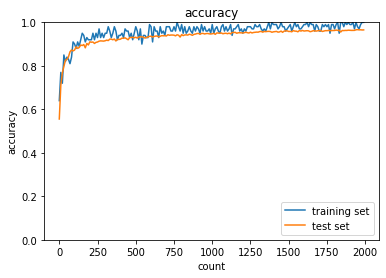Sigmoid-Heの組み合わせは学習が早くなり、ReLU-Xavierについてはあまり変化が見られないか？ 初期化のスケーリングの違いが√2倍がはいるかどうかなので、そこまで大きな違いが出ず、最初のランダムサンプリングの影響が強く出た可能性がある。 何度か試して平均的な傾向を確認する必要があると思われる。

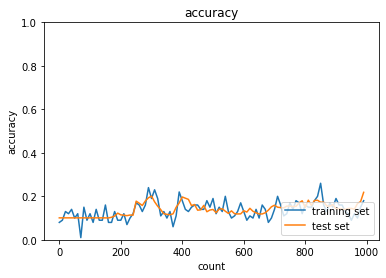
2_3_batch_normalization.ipynb

	バッチ正規化あり	バッチ正規化無し
sigmoid-Xavier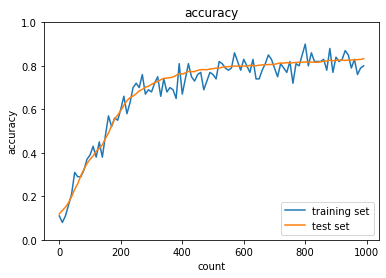
ReLU-He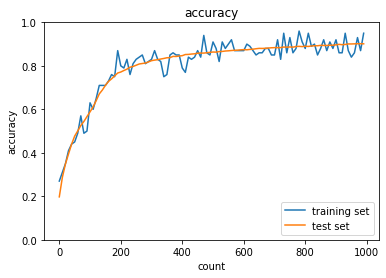
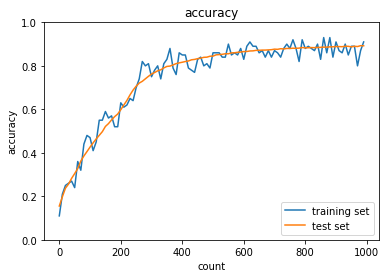Sigmoid-Xavier のケースではバッチ正規化無しで学習が進んでいないため、内部共変量シフトか勾配消失が起こってしまっていると考えられる。
ReLU関数の利用で改善されていること、そもそも層がそこまで深くなく内部共変量シフトがおこるほどではないことから勾配消失が起こっていたのではないかと考えられる。

2_4_optimizer.ipynb

Optimizerを変更してMNISTデータを予測するモデルの学習を行った結果を以下に示す。

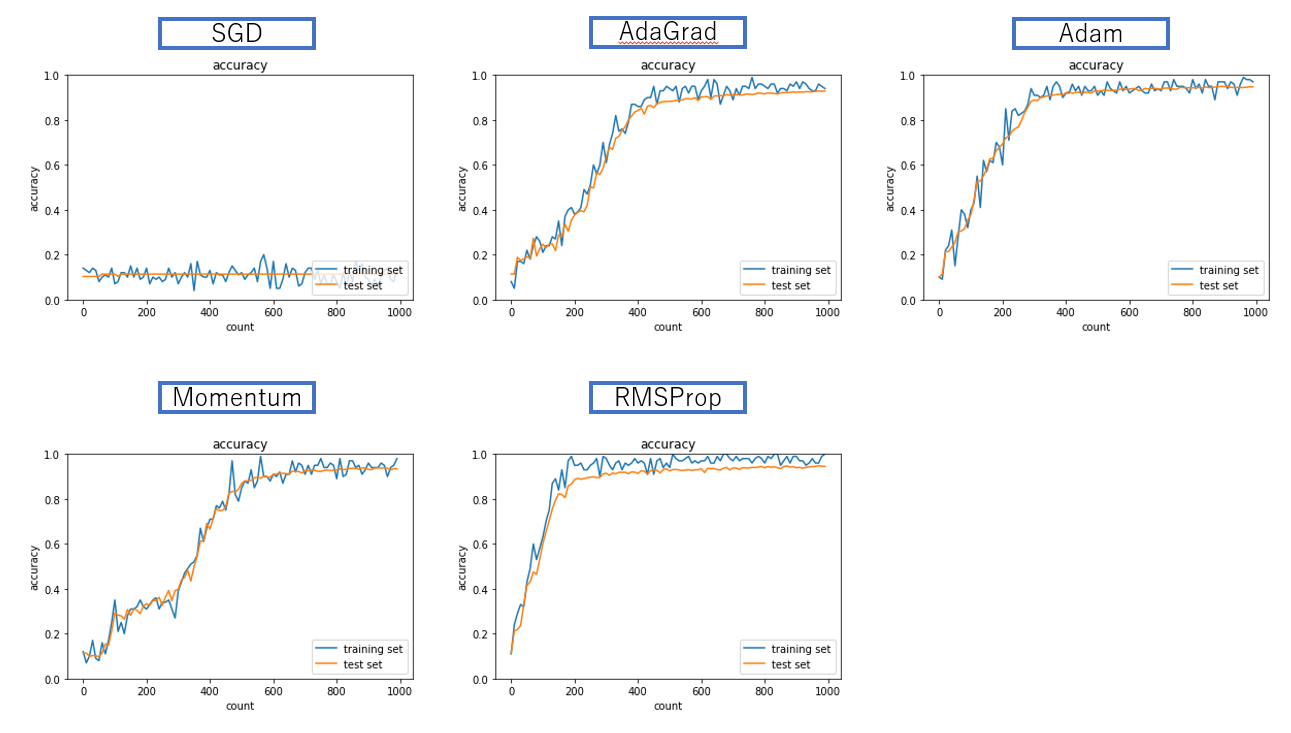
• SGDではそもそも学習がうまく行っていない。
• Momentumでは学習は進むが、かなり精度が変動していることがわかる
• AdaGradは学習率の減衰パラメータが誤差関数の傾きの二乗の累積であるためにRMSPropに比べて学習が遅くなる傾向が見られた
• AdaGradおよびRMSPropは訓練精度＞テスト精度の傾向があり、局所最適解に陥った可能性がある

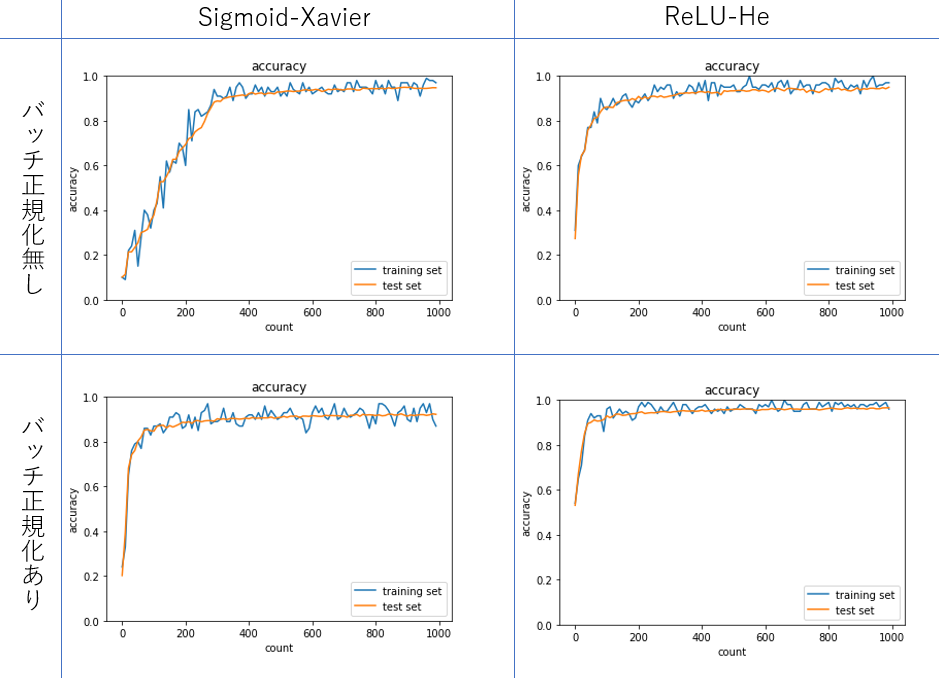
try:活性化関数と重みの初期化方法の変更とバッチ正規化

バッチ正規化をすることで学習の速度の向上が見られた。 ReLUとSigmoidではReLUのほうが学習速度がはやく、最終的な精度も良かった。

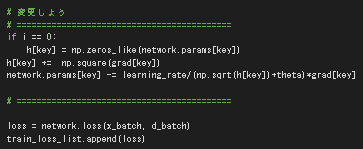
MomentumのコードをもとにAdaGradを作る

以下の様に変更した。

2_5_overfiting.ipynb

正則化と荷重減衰の強さ

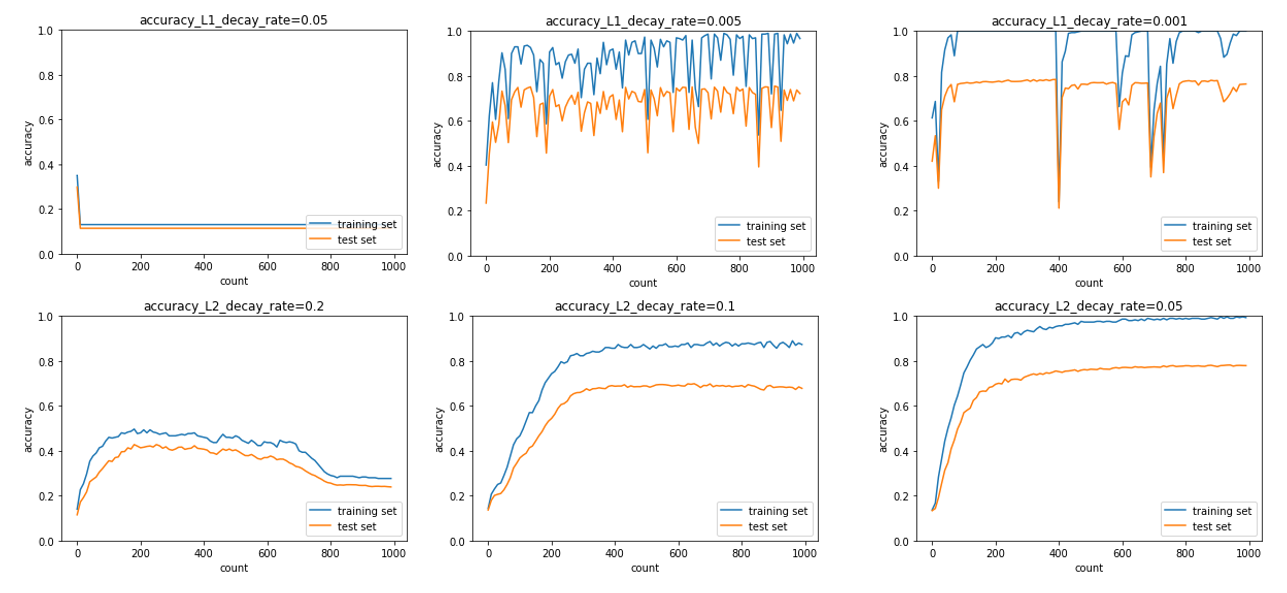L1正則化はスパース化で特徴量への制約がかなり強く働くので、より正則化の強さの設定に敏感に効いて来ると考えられる。 また、特徴量空間に描かれる誤差関数の曲面がなめらかでなくなるためか、精度の振動が激しい。

ドロップアウトの利用

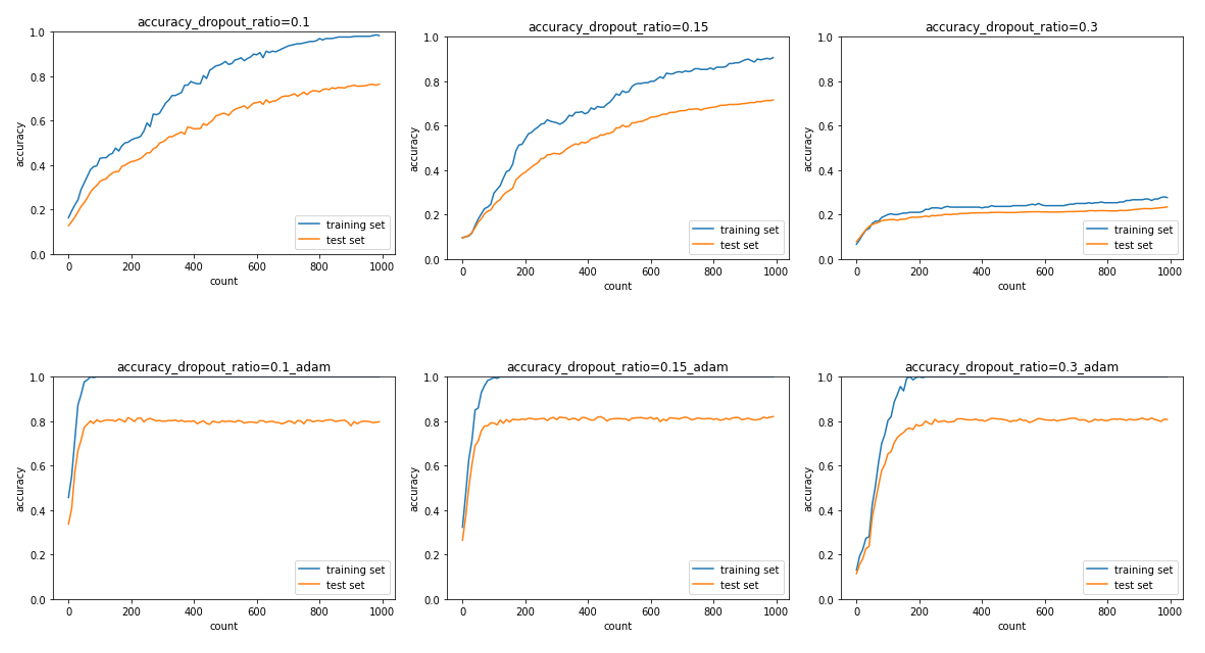同じドロップアウト比率を使っていても最適化器の違いでかなりの精度差がうまれた。 SGDで学習をしたときはまだ右肩上がりの状態で学習が終了していたため、Adamに切り替えたことで学習が収束するまで進んだことも一員として効果があるのでは無いかと考える。 また、ドロップアウトで学習中の誤差関数をもとに描かれる曲面の形状がいくらか変わるはずなので、局所最適解や鞍点などの問題に陥りやすいSGDはより学習が進みにくかったのでは無いかと考えられる。

dropout+L1

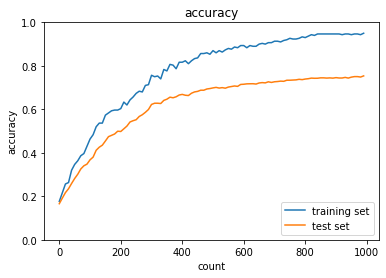
2_6_simple_convolution_network_after.ipynb

np.padの第二引数は各次元の前後にどれだけの長さのパディングをするか。

try：im2colの処理を確認しよう

・関数内でtransposeの処理をしている行をコメントアウトして下のコードを実行してみよう ・input_dataの各次元のサイズやフィルターサイズ・ストライド・パディングを変えてみよう

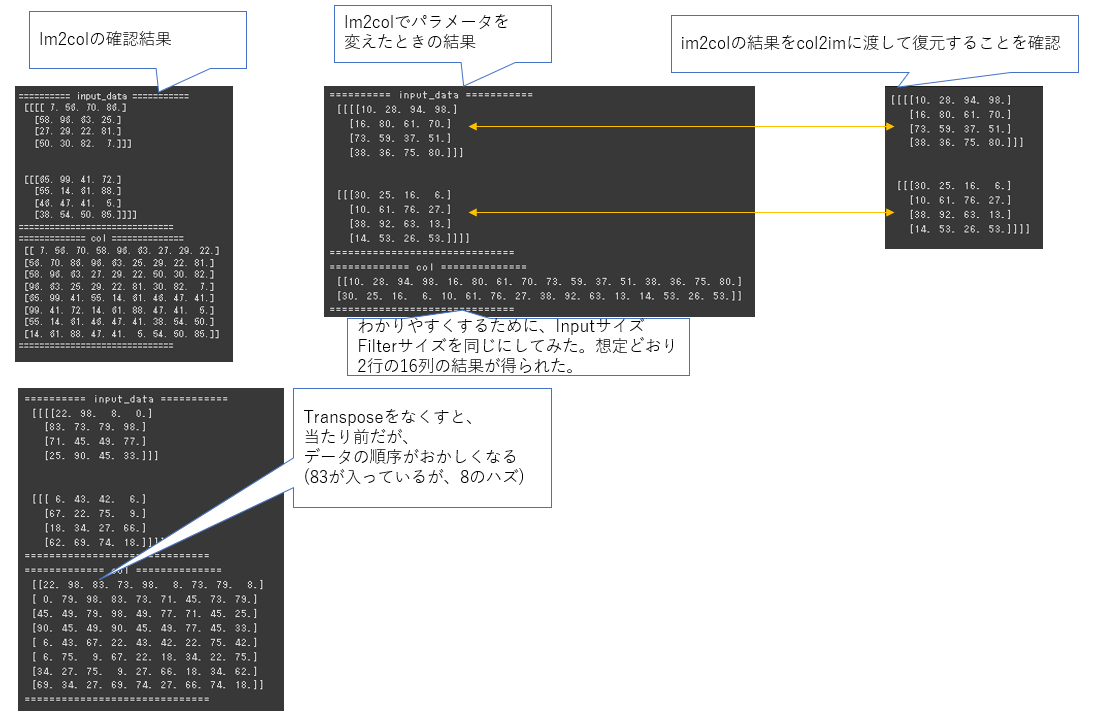
convolution class

forward処理ではフィルタリングが要素積の和になるので、和を取りたい範囲の次元を1次元配列化して内積を取るような処理になるようにインプットとフィルタの形状やデータ順序を変更している。 backward処理も基本的に同様でforwardでした内容の逆をして計算をし易い状態にしてから通常のNNのBackward処理をして、形状を戻すことをしている。。

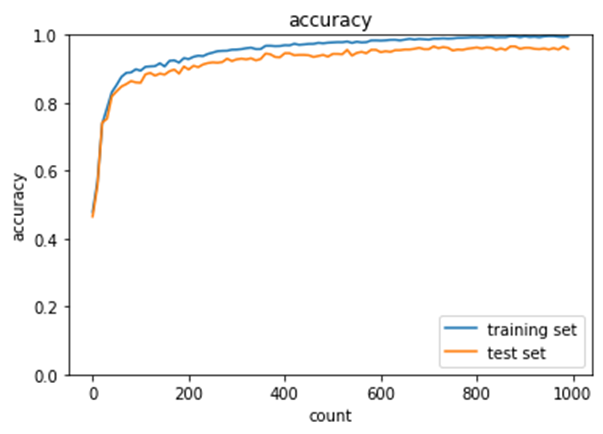
2_7_double_convolution_network_after.ipynb

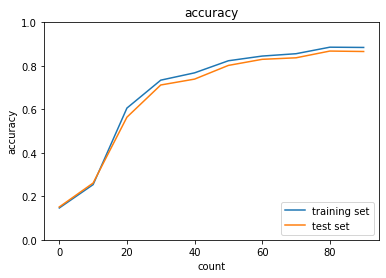
2_8_deep_convolution_net.ipynb

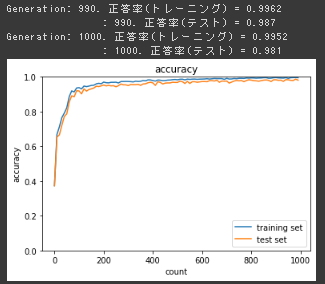
2_9_regularization.ipynb

CIFAR10 の画像分類タスクに対して各種正規化を適用。

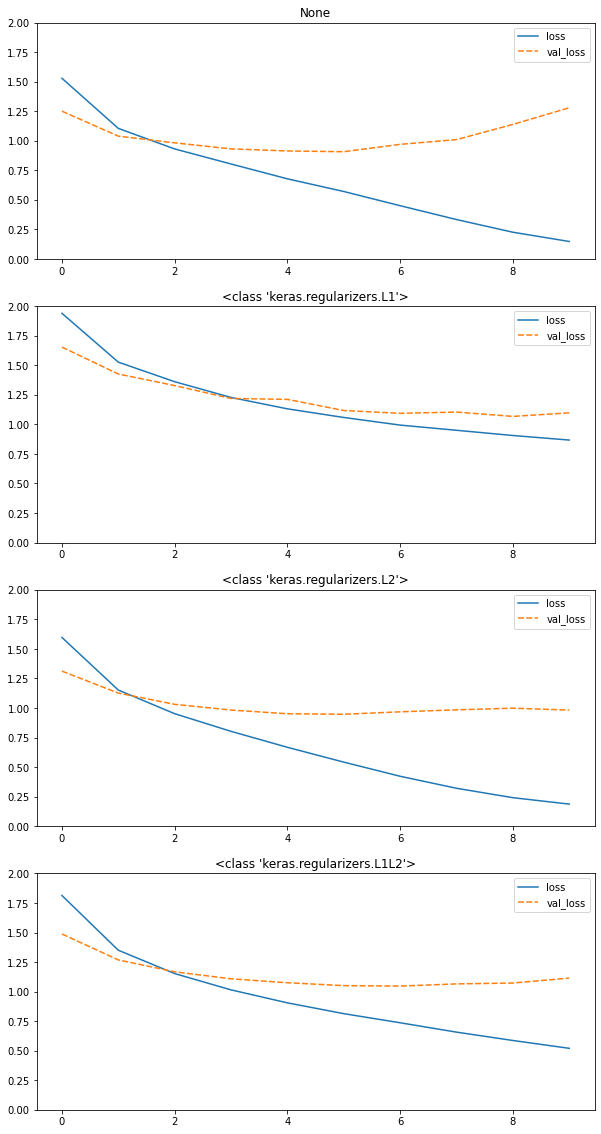正規化を適用していないモデルでは、学習が進むに連れテスト誤差が上がってきてしまっているが、 L1,L2及びErasticNetではそれが抑制できていることがわかる。

2_10_layer-normalization.ipynb

レイヤ正規化自体の説明はプラスアルファのところに記載。

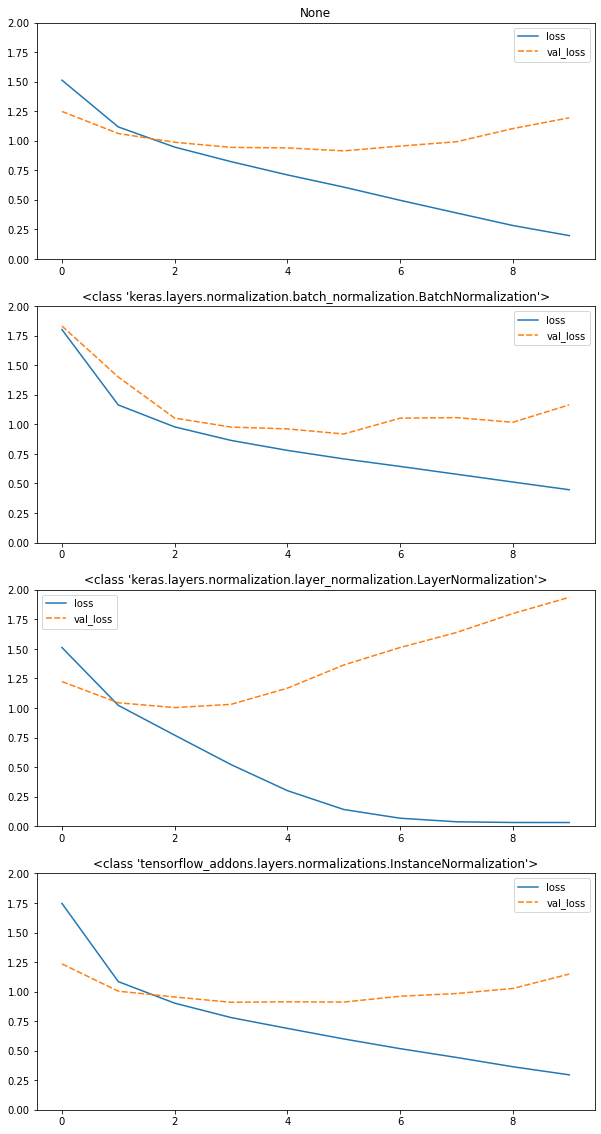レイヤ正規化では過学習が発生しているようだが、特徴量次元方向で正規化した結果、確信度が低い特徴量の切り捨てが多く発生したのでは無いかと考えられる。インスタンス正規化の方はあまりその傾向が見られないため、その可能性は高いのでは無いかとおもう。

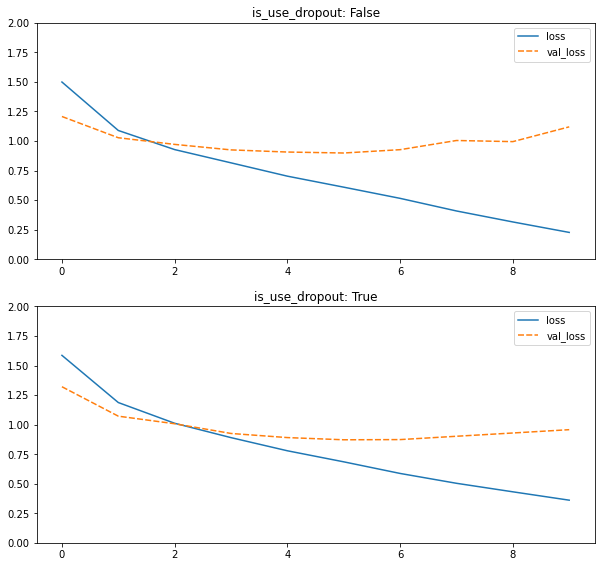
2_11_dropout.ipynb

ドロップアウト比率0.3での比較。 無しでテスト誤差1.25→ありで1.0で確かに過学習が抑制されていることがわかる。 実装箇所は最終の全結合層の直前。

2_app_1_tensorflow_codes_after.ipynb

tensorflowでの実装

定数定義

tensorflow.constant(value)

変数定義

tensorflow.Variable(value)

計算グラフの定義

tensorflow.functionデコレータを使って関数定義する

@tf.function
def add(a,b):
	return a+b

optimizer

tensorflow.keras.optimizersのなかから選択

訓練ステップ

こちらもtensorflow.funcitonデコレータを用いる。 GradientTape()というクラスのgradient(損失関数,訓練パラメータのリスト)メソッドで勾配を得る oplimizers内のクラスが持つapply_gradientsメソッドに（勾配、勾配に対応するパラメータ）のタプルを返すイテレータを与えることでパラメータの更新を行う。

@tf.function
def train_step(inputs, labels):
    with tf.GradientTape() as tape:
        y = linear_regression(inputs, W, b)
        loss = calc_loss(y, labels)
    gradients = tape.gradient(loss, trainable_variables) # 勾配 (loss を trainable_variables の各変数で微分) を求める

    optimizer.apply_gradients(zip(gradients, trainable_variables)) # 勾配を用いて変数の更新

    return loss

2_app_2_save_load.ipynb

tensorflowでの実装の続き

モデルの保存

tensorflow.train.Checkpointクラスの利用 インスタンス生成時に与えるのはモデルでも、変数の辞書でも可。 .save(パス)メソッドで保存 .restore(パス)メソッドで復元

ckpt = tf.train.Checkpoint(step=tf.Variable(1), optimizer=opt, net=net, iterator=iterator)
manager = tf.train.CheckpointManager(ckpt, './tf_ckpts', max_to_keep=3)

（トレーニングのチェックポイント  |  TensorFlow Core より引用）

2_app_3_keras_codes_after.ipynb

tensorflow.keras.models.Sequentialクラスを用いた 深層学習モデルの設計方法を学んだ。

1. Sequentialクラスでモデルインスタンスを生成
2. .addメソッドでtensorflow.keras.layersモジュールにあるレイヤクラスを追加していく
3. .compileメソッドで損失関数、オプティマイザ、評価指標の設定を行う
4. .fitメソッドでモデルの学習

プラスアルファ

レイヤ正規化

実装演習内で レイヤ正規化という言葉が新しく出てきたので、 Layer Normalizationを理解する | 楽しみながら理解するAI・機械学習入門を参考にまとめる。

バッチ正規化 で残った以下の問題に対応するための手法

• ミニバッチごとの平均分散を計算するので、バッチサイズが小さいときに平均・分散が不安定になる
• RNNに適応するのが難しい（サンプル長が可変）

以上に対応するために バッチ正規化ではサンプル次元の方向で系列をとって平均分散を計算していたのを、 特徴量次元の方向で系列を取って平均分散を計算するようにしている。 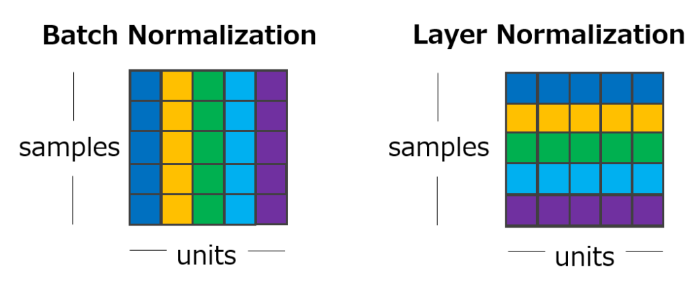(Layer Normalizationを理解する | 楽しみながら理解するAI・機械学習入門より引用）

各種正規化の図解

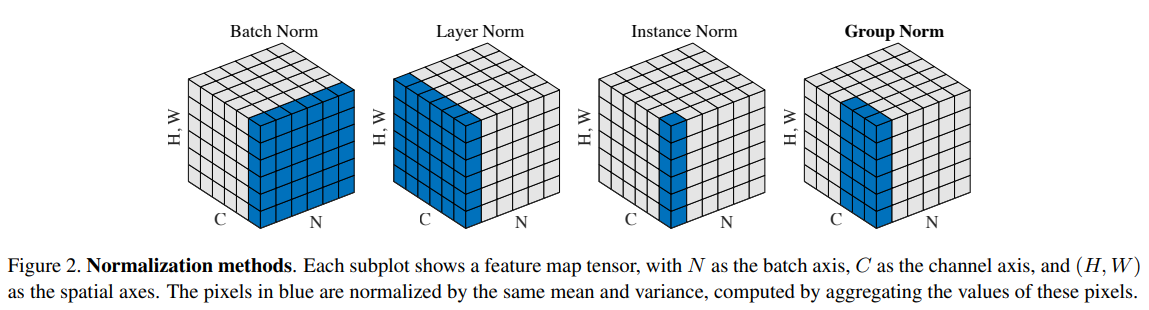(Group Normalization(https://arxiv.org/abs/1803.08494)より引用)

各種正規化の使われ方

• バッチ正規化：幅広いタスクで使用、ただしバッチサイズが小さいときに安定しないことから、近年の大規模モデルでバッチサイズが大きくできないときに他の手法に置き換えられる。
• レイヤ正規化：時系列モデル
• インスタンス正規化：Style Transferで利用。各データサンプルが同じようなコントラストになるように変換される

Erastic Net

L1正則化とL2正則化を混ぜ合わせた正則化手法、