DeepLearningDay3
再帰型NNの概念
再帰型NN→RNN
時系列データとは
時間的順序を追って一定間隔ごとに観察され、 相互に統計的依存関係が認められるようなデータの系列
時系列データの例
- 音声データ
- テキストデータ
RNNの全体像
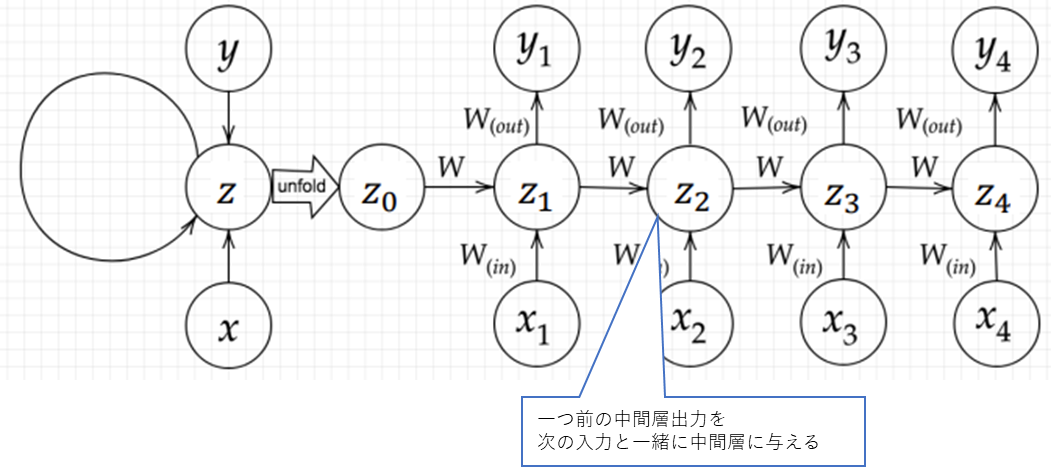 (講義スライドより引用)
(講義スライドより引用)
$u^t = W_{(in)}x^t + W{z^{t-1}} + b$ $z^t = f(W_{(in)}x^t + Wz^{t-1} + b)$ $v^t = W_{(out)} z^t + c$ $y^t = g(W_{(out)} z^t + c)$
$W_{(in)}$:入力層から中間層への重み $W_{(out)}$:中間層から出力層への重み
u[:,t+1] = np.dot(X,W_in) + np.dot(z[:,t].reshape(1,-1),W) + b
z[:,t+1] = functions.sigmoid(u[:,t+1])
v = np.dot(z[:,t+1].reshape(1,-1),W_out)
y[:,t] = functions.sigmoid(v + c)
※実装上は1次元目がデータ列になるため、重みに対して左から入力を掛ける形になる。
RNNの特徴
初期の状態と過去の時間t-1の状態を保持し、そこから次の時間でのtを再帰的に求める再帰構造をもつ
BPTT (Back Propagation Through Time)
BPの復習
誤差を微分のチェインルールに従って、誤差から逆算していくことで不要な再起的計算を避けて微分を算出できる。
BPTTの数学的記述
※(パラメータ更新と合わせて、実装例と一致するように、数式展開で確認しながら表現変えてます) 誤差関数を3つの重みと2つのバイアスでそれぞれ微分する。
$$\frac{\partial E^t}{\partial W_{(in)}} = \frac{\partial E^t}{\partial u^t}\left[\frac{\partial u^t}{\partial W_{(in)}}\right]^T = \sum_{0\leq k \leq t} \delta^{k}\cdot x^{k}$$
$$\frac{\partial E^t}{\partial W_{(out)}} = \frac{\partial E^t}{\partial v^t}\frac{\partial v^t}{\partial W_{(out)}} = \delta^{out, t}\cdot z^t$$
$$\frac{\partial E^t}{\partial W} = \frac{\partial E^t}{\partial u^t}\left[\frac{\partial u^t}{\partial W}\right]^T= \sum_{0\leq k \leq t} \delta^{k}\cdot z^{k-1}$$
$$\frac{\partial E^t}{\partial b} = \frac{\partial E^t}{\partial u^t} \left[\frac{\partial u^t}{\partial b}\right]^T = \sum_{0\leq k \leq t} \delta^{k}$$
$$\frac{\partial E^t}{\partial c} = \frac{\partial E^t}{\partial v^t} \frac{\partial v^t}{\partial c} = \delta^{out, t} \cdot 1 = \delta^{out, t}$$ ※$\delta^t = \frac{\partial E}{\partial u^t}$ ,$\delta^{out, t} = \frac{\partial E}{\partial v^t}$とおいている。$\left[\right]^T$は転置ではなく、時間に遡って微分という意味。新しい処理が入ったというよりも、$u_t$にかかわるパラメータは過去時刻の中間層出力zを介して時間を遡る必要があることを明示しているだけ。
$$ \frac{\partial E^t}{\partial u^t} = \frac{\partial E^t}{\partial v^t} \frac{\partial v^t}{\partial u^t}=\frac{\partial E^t}{\partial v^t} \frac{\partial{W_{(out)}f(u^t) + c}}{\partial u^t} = \delta^{out, t} f’(u^t)W^T_{(out)} = \delta^t $$
# 1つ目の計算方法
delta[:, t] = np.dot(delta_out[:, t].T, W_out.T) * functions.d_sigmoid(u[:, t])
# 2つめの計算方法
delta[:, t] = np.dot(delta[:, t+1].T, W.T) * functions.d_sigmoid(u[:, t])
"""
スライド中ではなぜか和をとって代入していたが、数式的におかしいのでは?
2で割ってればわからなくも無いがあえてやる必要も無いと思う。
"""
中間層~中間層の重みと入力層の重みは時間的に遡って誤差を逆伝播させるので、前の時間との関係式を確認 する。
$$ \delta^{t-1} = \frac{\partial E^t}{\partial u^{t-1}} = \frac{\partial E^t}{\partial u^t} \frac{\partial u^t}{\partial u^{t-1}} $$
$$ = \delta^t\left{ \frac{\partial u^t}{\partial z^{t-1}} \frac{\partial z^{t-1}}{\partial u^{t-1}} \right} = \delta^t {W f’(u^{t-1})} $$
$$ \delta^{t-k-1} = \delta^{t-k}{Wf’(u^{t-k-1})} $$ ※kはt-1以下の任意の定数
パラメータ更新
上の式で各時刻tに対して行っていたのを全域にわたって和を取ってパラメータ更新する。
$$W^{new}{(in)} = W^{old}{(in)} - \epsilon \sum_{0\leq t \leq \tau}\frac{\partial E^t}{\partial W_{(in)}} = W^{old}{(in)} - \epsilon \sum{0\leq t \leq \tau} \sum_{0\leq k \leq t} \delta^{k}\cdot x^{k}$$
$$W^{new}{(out)} = W^{old}{(out)} - \epsilon \sum_{0\leq t \leq \tau}\frac{\partial E^t}{\partial W_{(out)}} = W^{old}{(out)} - \epsilon \sum{0\leq t \leq \tau}\delta^{out, t}z^t$$
$$W^{new} = W^{old} - \epsilon \sum_{0\leq t \leq \tau}\frac{\partial E}{\partial W} = W^{old} - \epsilon \sum_{0\leq t \leq \tau} \sum_{0\leq k \leq t} \delta^{k}\cdot z^{k-1}$$
$$b^{new} = b^{old} - \epsilon \sum_{0\leq t \leq \tau}\frac{\partial E}{\partial b} = b^{old} - \epsilon \sum_{0\leq t \leq \tau} \sum_{0\leq k \leq t} \delta^{k}$$
$$c^{new} = c^{old} - \epsilon \sum_{0\leq t \leq \tau}\frac{\partial E}{\partial c} = c^{old} - \epsilon \sum_{0\leq t \leq \tau}\delta^{out, t}$$
LSTM
BPTTの一つ前の時刻のδを求める式を見るとわかる様に、ワンステップ戻るのに活性化関数の導関数と重みを掛ける計算になっているため、時系列を遡るほど勾配消失問題が起こりやすくなる。 →長い時系列の学習が困難。
上記の課題を解決するための新しい構造がLSTM
LSTMの全体像
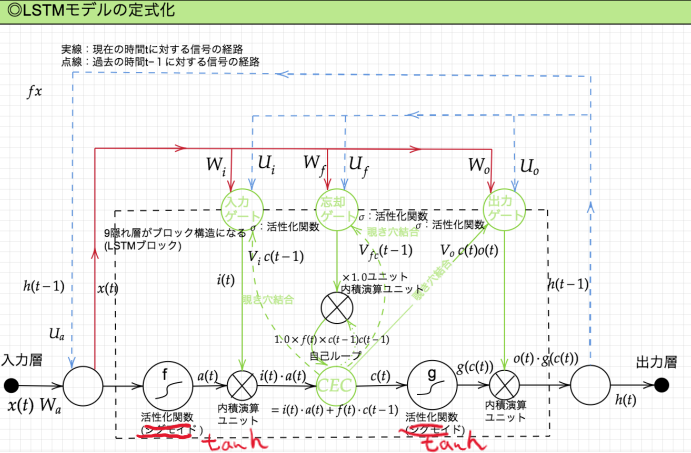 (講義スライドより引用)
※活性化関数
(講義スライドより引用)
※活性化関数
- 各ゲートはマスク処理なので0~1のスケーリングを行うシグモイド
- それ以外の活性化関数はハイパボリックタンジェントになる。
CEC
Constant Error Caroucel:誤差カルーセル
勾配消失問題及び、勾配爆発問題の解決方法として勾配が1であれば良い。
$$ \delta^{t-z-1} = \delta^{t-z}\left{W f’(u^{t-z-1})\right}=1 $$ $$ \frac{\partial E}{\partial c^{t-1}} = \frac{\partial E}{\partial c^t} \frac{\partial c^t}{\partial c^{t-1}} = \frac{\partial E}{\partial c^t} \frac{\partial}{\partial c^{t-1}}{a^t - c^{t-1}} = \frac{\partial E}{\partial c^t} $$
課題
ニューラルネットワークの学習特性が無い (入力データについて時間依存度に関係なく重みが一律であるため)
入力ゲートと出力ゲート
目的:CECの学習特性がない問題を解決する、重み衝突への対応 方法:各ゲートへの入力値への重みをW,前回の隠れ層の出力への重みをUで可変とする
※重み衝突とは、特徴が短期的なものか長期的なものか判断できず、重みを適切に調節できないこと
忘却ゲート
過去情報がいらなくなった時点でその情報を忘却する機能 (LSTMのCECに過去情報が不要になっても保持されている問題に対応するため)
のぞき穴結合
Peephole Connectionのこと
目的
- CEC自身の値もゲート制御に使う
- CECの値を忘却させたり利用するタイミングの自由度を上げる 各ゲートの入力が短期記憶の前回中間層出力と入力の線形結合だったところにCECの線形結合も加える。
※あまり性能向上は見られないとのこと
GRU
LSTMのパラメータを大幅に削減し、同等からそれ以上の性能を望める様になった構造
メモリは今回更新する分を前回メモリから除く構造になっている。
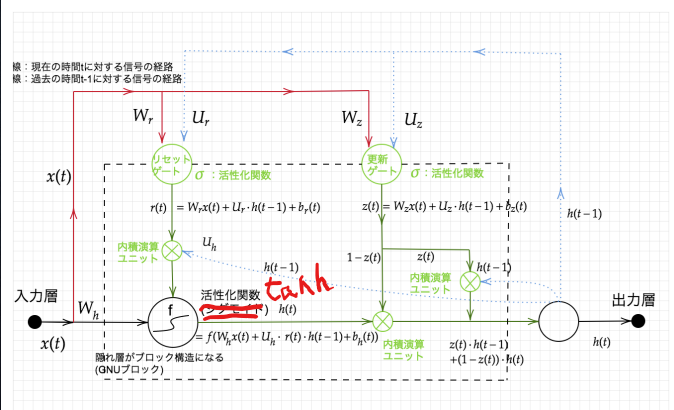 (講義スライドより引用)
(講義スライドより引用)
隠れ層の状態 これと前回の隠れ層出力の加重平均を新たな隠れ層出力とする
$$ h_{tmp}(t) = f(W_h x(t) + U_h \cdot (r(t) \cdot h(t-1)) + b_h(t)) $$
リセットゲートの出力
$$ r(t) = W_r x(t) + U_r \cdot h(t-1) + b_r(t) $$ 更新ゲートの出力
$$ z(t) = W_z x(t) + U_z \cdot h(t-1) + b_z(t) $$ 隠れ層からの出力 (1ステップ前の中間表現と計算された中間表現の線形和) $$ h(t) = z(t) \cdot h(t-1) + (1-z(t)) \cdot h(t) $$
双方向RNN
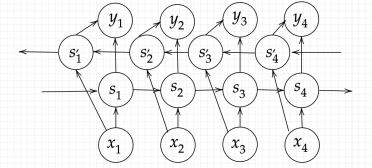 (講義スライドより引用)
(講義スライドより引用)
未来側から戻ってくる隠れ層を追加する。 文脈などを考慮することができ、精度が上がるがデータ系列が揃ってからという制約が追加されるため適用可能なタスクの範囲は狭まる。 機械翻訳や文章の推敲に使われる。
※順方向と逆方向に伝播したときの中間層表現を合わせたものが特徴量 → 実装時は、特徴量次元のaxis=1でconcatenateする 0番目が系列方向、1番目が特徴方向
Seq2Seq
Encoder-Decoderモデル 機械翻訳に使われる
Encoder-RNN
機械翻訳の例での説明
Input:テキストデータ
- Tokenize:単語レベルに分割する
- One-hot coding: 各単語のone-hotベクトル化
- Embedding: 分散表現ベクトルにする
- 学習によって200~300程度の長さのベクトルにする(次元削減)
- 意味の近いものをまとめる
- Encoder-RNN:通常のRNNと同様に単語ベクトル系列を与えていき、最後のベクトルを与えたときのHidden Stateを文脈ベクトル(Final State,Thought Vector)とする
著名なモデル
BERT(Bidirectional Encoder Representations from Transformers) :Googleによって提案された自然言語処理モデル。双方向の文脈理解、汎用性、(ラベルが不要なことから)データ不足への対応というメリットがある。
- MLM(Masked Language Model):単語系列のいち部を除いて前後の系列から予測させるように学習させる
- NSP(Next Sentence Prediction): 単語ではなく文のレベルで学習させるために、2つの入力分に対してその2文が隣り合っているかを予測させるタスクを与える。 (参考:BERTとは|Googleが誇る自然言語処理モデルの仕組み、特徴を解説 | Ledge.ai)
Decoder-RNN
- Encoder-RNNのFinal Stateから各単語の生成確率を出力していく
- 生成確率に従って各単語をランダムに選ぶ
- 生成された単語をenbeddingしてDecoder-RNNの次の入力とする
- 上記を最後の単語が生成されるまで繰り返す
HRED
1文レベルでの回答しかできないというSeq2Seq の課題に対応する →会話全体の文脈を把握したい
HRED = Seq2Seq + Context RNN ※Context RNNはEncoder-RNNのFinal Stateの系列をまとめてこれまでの会話コンテキスト全体を表すベクトルに変換する構造
問題点
- 出力の多様性が多少の表現レベルでしかなく、会話の展開レベルでの多様性がない
- 短く情報量に乏しい答えを出しがち
VHRED
HREDの問題点に対応するために、VAEの潜在変数の概念を追加したもの
VAE
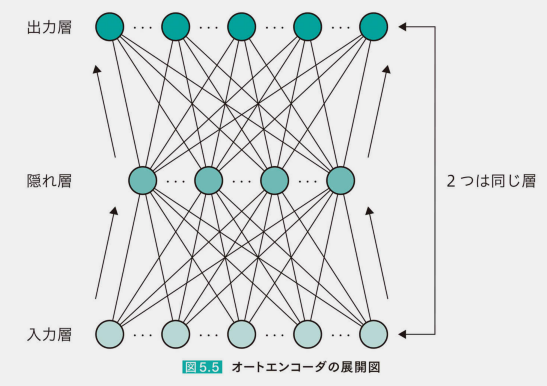
オートエンコーダ
隠れ層を潜在変数zとする
自己符号化器とも言われる。 入力と同じ出力を返す二層のネットワーク
隠れ層は入力の次元圧縮になる。
 (猪狩 宇司; 今井 翔太; 江間 有沙; 岡田 陽介; 工藤 郁子; 巣籠 悠輔; 瀬谷 啓介; 徳田 有美子; 中澤 敏明; 藤本 敬介; 松井 孝之; 松尾 豊; 松嶋 達也; 山下 隆義. 深層学習教科書 ディープラーニング G検定(ジェネラリスト)公式テキスト 第2版 (Kindle の位置No.3985-3986). 株式会社 翔泳社. Kindle 版. )
(猪狩 宇司; 今井 翔太; 江間 有沙; 岡田 陽介; 工藤 郁子; 巣籠 悠輔; 瀬谷 啓介; 徳田 有美子; 中澤 敏明; 藤本 敬介; 松井 孝之; 松尾 豊; 松嶋 達也; 山下 隆義. 深層学習教科書 ディープラーニング G検定(ジェネラリスト)公式テキスト 第2版 (Kindle の位置No.3985-3986). 株式会社 翔泳社. Kindle 版. )
VAEの特徴
潜在変数zに確率分布z~N(0,1)を仮定し確率分布という構造に押し込めたもの 元のデータの分布(近さや遠さ)が潜在変数の分布にも反映されてほしい
Word2Vec
単語をベクトルで効率的に表現するための手法
- RNNの各時点での入力は可変長でなく固定長である必要がある →単語を文字コードに基づくビットの系列ではなく一つのベクトルとして表現する
- 辞書で一対一対応させるone-hotベクトルはデータ利用効率が低い →分散表現学習によりデータ量の削減
Attention Mechanism
Seq2Seqでは長い入力系列でも短い入力系列でも同じ内部表現に押し込む必要があり、 長い入力系列において関連性を保持することが困難であった。
Attention Mechanismは上記の問題に対応するための入力系列と出力系列の関連を見つけるための仕組み
VQ-VAE
VQ-VAE:潜在変数を離散的な数値になるように学習させる VAE:潜在変数をガウス分布に従う様に学習させる
この離散的な数値に対応させることをVector Quantization(ベクトル量子化処理)という
VQ-VAEのアーキテクチャ
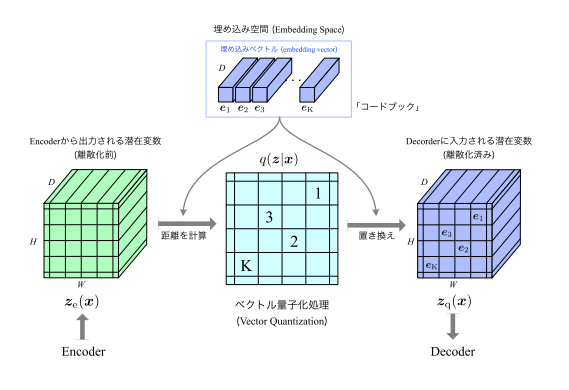 (講義資料より引用)
(講義資料より引用)
VQの手順
- Encoderから出力される離散化前の潜在変数と事前に用意されているK個の埋め込みベクトルの距離(L2ノルム)を算出する
- 潜在変数をK個の埋め込みベクトルのうち最も近い(似ている)ベクトルに置き換える
$$ z_q(x) = e_k $$
$$ k = \underset{j}{argmin} ||z_e(x)-e_j||^2 $$
目的
- 適切なデータ表現の獲得:自然界の特徴を捉えるにおいて、離散的な表現が適していると想定されることから。
- Posterior_Collapseを防ぐ
VAEをPixel CNNなどの強力なデコーダーと組み合わせたときに、潜在変数がデータの特徴をうまく捉えられなくなる現象。 VQ-VAEで離散的な潜在変数を学習するようにすることで回避できるとされる
学習
損失関数
[!inote]- ベースラインとしてVAEでのELBOから出発して、 Vector-Quantizationに伴う誤差項を追加したものを損失関数とする ELBOのKLダイバージェンスと再構成誤差については事前分布を1/Kで固定することと事後分布がone-hotベクトルであることからKLダイバージェンスが定数になるため再構成誤差のみが学習に関係する Vector-Quantizationに伴う誤差項は以下の2つ
- Codebook Loss = $ \left|\operatorname{sg}\left[\boldsymbol{z}{\mathrm{e}}(\boldsymbol{x})\right]-\boldsymbol{e}\right|{2}^{2} $:埋め込みベクトルの更新に用いる
- Commitment Loss = $ \beta\left|\boldsymbol{z}{\mathrm{e}}(\boldsymbol{x})-\operatorname{sg}[\boldsymbol{e}]\right|{2}^{2} $: Encoderネットワークの更新に用いる
$$ \mathcal{L}{\mathrm{VQ}-\mathrm{VAE}}=\log p\left(\boldsymbol{x} \mid \boldsymbol{z}{\mathrm{q}}(\boldsymbol{x})\right)+\left|\operatorname{sg}\left[\boldsymbol{z}{\mathrm{e}}(\boldsymbol{x})\right]-\boldsymbol{e}\right|{2}^{2}+\beta\left|\boldsymbol{z}{\mathrm{e}}(\boldsymbol{x})-\operatorname{sg}[\boldsymbol{e}]\right|{2}^{2} $$
損失関数の導入
VAEと同様にELBO (Evidence Lower BOund)の最大化でEncoder、Decoderの学習を行うことを考える。
$$ \mathcal{L}{\mathrm{ELBO}}=\mathbf{K L}(q(z \mid \boldsymbol{x}) | p(z))+\log p\left(\boldsymbol{x} \mid \boldsymbol{z}{\mathrm{q}}(\boldsymbol{x})\right) $$ 第一項は事後分布と事前分布のKLダイバージェンス、2項目は再構成誤差を表す。
!memo 結果的に第1項は定数となるため、第二項の再構成誤差について考えることになる。
第一項のカルバックライブラーダイバージェンスの計算は、
- 事前分布$p(z)=1/K$の一様分布であると固定
- $q(z=k \mid \boldsymbol{x})$がone-hotベクトル ※総和記号の中身 $[q(z=k \mid \boldsymbol{x}) \log q(z=k \mid \boldsymbol{x})]$ は、 $0 \log 0$ か $1 \log 1$ となる 上記2点を考慮することで以下のようにまとめることができ、定数となる。
$$
\begin{aligned}
\mathbf{K L}(q(z \mid \boldsymbol{x}) | p(z)) & =\mathbb{E}{z \sim q(z \mid \boldsymbol{x})}\left[\log \frac{q(z \mid \boldsymbol{x})}{p(z)}\right] \
& =\sum{k=1}^{K} q(z=k \mid \boldsymbol{x}) \log q(z=k \mid \boldsymbol{x})-\sum_{k=1}^{K} q(z=k \mid \boldsymbol{x}) \log p(z=k) \
& =-\log \frac{1}{K} \sum_{k=1}^{K} q(z=k \mid \boldsymbol{x}) \
& =-\log \frac{1}{K}=\log K
\end{aligned}
$$
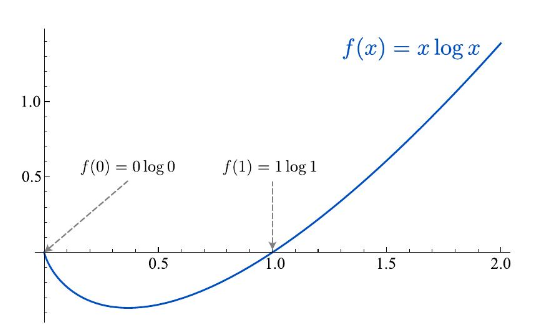
(講義資料より引用:KLダイバージェンスの計算の2行目の第一項が0になる説明)
フレームワーク演習:双方向RNN/勾配のクリッピング
データセットの読み込み
- tensorflow_datasetsをインポート
- 以下の関数で訓練、評価、テストセットを作成する
tensorflow_datasets.load(dataset_name,split=['train[:x%]','valid[x%:y%]','test[y%:]']) - イテレータとすることで一つずつ取り出せるようにする。
データの前処理
- 音声データは長さがまちまちなので、モデルに入力できるようにするために固定の長さに揃える
- tensorflow.data.Datasetオブジェクトにある.map(funtion)メソッドで一つひとつのデータに対して処理を加える
- map関数で引数に与える関数内ではtensorflow.cond(tf.greaterなどの条件,条件が真のときの処理,偽のときの処理)関数などを用いて前処理を行う
- .batchメソッドでミニバッチを構成する
モデルの定義
- tensorflow.keras.models.Sequantialクラスを使ってモデルのインスタンスを生成
- addメソッドで層を追加。 ※tensorflow.keras.layers内のクラスを使う Module: tf.keras.layers | TensorFlow v2.12.0 ※双方向のレイヤーを追加したいときは.add(layers.Bidirectional(追加したい層))という形で追加する
- (summaryメソッドで定義したモデルの概要の確認)
モデルの学習
- .compileメソッドを用いてロス関数、オプティマイザー、評価指標の設定を行う ※勾配クリッピングについてはオプティマイザーの領域の話であるため、オプティマイザの引数clipvalueに値を与えることで実装できる
- .fitメソッドに準備したデータセットを与えて学習を進める
フレームワーク演習:Seq2Seq
系列入力としてsin関数、出力としてcos関数を予測させる。
モデルの実装
今回においては入力から出力が一本道ではないため、Sequentialは使わず、 tf.keras.Inputから始めて、順伝播の経路に従って関数に引数を与え, 最後にtf.keras.models.Model(inputs,outputs)関数でまとめる形式で実装を行った。
tf.keras.backend.clear_session()
# エンコーダー
e_input = tf.keras.layers.Input(shape=(NUM_STEPS, NUM_ENC_TOKENS), name='e_input')
_, e_state = tf.keras.layers.SimpleRNN(NUM_HIDDEN_PARAMS, return_state=True, name='e_rnn')(e_input)
# デコーダー
d_input = tf.keras.layers.Input(shape=(NUM_STEPS, NUM_DEC_TOKENS), name='d_input')
d_rnn = tf.keras.layers.SimpleRNN(NUM_HIDDEN_PARAMS, return_sequences=True, return_state=True, name='d_rnn')
d_rnn_out, _ = d_rnn(d_input, initial_state=[e_state])
# 全結合
d_dense = tf.keras.layers.Dense(NUM_DEC_TOKENS, activation='linear', name='d_output')
d_output = d_dense(d_rnn_out)
model_train = tf.keras.models.Model(inputs=[e_input, d_input], outputs=d_output)
model_train.compile(optimizer='adam', loss='mean_squared_error')
model_train.summary()
データの準備
訓練時
[!note]- 訓練時と推論時では異なることに注意
- デコーダーの入力には最初の入力がエンコーダーに最後の系列を入力したときの隠れ層の状態(文脈ベクトル)になるため、0番目の要素は飛ばして定義する
- 教師データがあるので各サンプルの1番目以降のデコーダー入力は出力系列と同じ
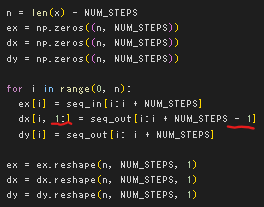
推論時
[!note]- 訓練時と推論時では異なることに注意
- エンコーダーとデコーダーでModelを分割して定義する
- 訓練時と異なり教師データをデコーダーに入力できないため、tf.keras.layers.Inputでデコーダー入力とデコーダーの隠れ層の状態を定義する
推論時の手順
- エンコーダーに入力系列を与えたときの最終の隠れ層の状態(文脈ベクトル)を取得する
- 文脈ベクトルをデコーダーの最初の隠れ層の状態、ゼロベクトルを入力として与える
- 以降デコーダーの出力と隠れ層の状態を次のステップの入力と隠れ層の状態として与えて1ステップのデータ長分だけ繰り返す
def predict(input_data):
state_value = model_pred_e.predict(input_data)
_dy = np.zeros((1, 1, 1))
output_data = []
for i in range(0, NUM_STEPS):
y_output, state_value = pred_d_model.predict([_dy, state_value])
output_data.append(y_output[0, 0, 0])
_dy[0, 0, 0] = y_output
return output_data
フレームワーク演習:Data-Augumentation
座標変換
反転
- tf.image.random_flip_left_right(image,seed:int)で左右反転
- tf.image.random_flip_up_down(image,seed:int)で上下反転 ※反転するかはランダム
回転
- tf.image.rot90(image, k=1)で反時計回りにk✕90°の回転
- tf.keras.preprocessing.image.random_rotationで角度指定なしの回転 ※imageのからarrayへの変換が必要
image = image_origin
array = tf.keras.preprocessing.image.img_to_array(image)
array = tf.keras.preprocessing.image.random_rotation(array, rg=360, row_axis=0, col_axis=1, channel_axis=2)
image = tf.keras.preprocessing.image.array_to_img(array)
画像の一部を活用・マスクする
- tf.image.random_crop(image,size=(int,int,int),seed:int)で切り抜きして入力画像とする
- 以下のrandom_erasing関数を使用してランダムな領域をマスクする 参考資料: “Random Erasing Data Augmentation”
def random_erasing(img, prob = 0.5, sl = 0.02, sh = 0.4, r1 = 0.2, r2 = 0.8):
if np.random.random() < prob:
return img
else:
H = img.shape[0]
W = img.shape[1]
S = H * W
while True:
S_e = S * np.random.uniform(low=sl, high=sh)
r_e = np.random.uniform(low=r1, high=r2)
H_e = np.sqrt(S_e * r_e)
W_e = np.sqrt(S_e / r_e)
x_e = np.random.randint(0, W)
y_e = np.random.randint(0, H)
if x_e + W_e <= W and y_e + H_e <= H:
img_modified = np.copy(img)
img_modified[y_e:int(y_e + H_e + 1), x_e:int(x_e + W_e + 1), :] = np.random.uniform(0, 1)
return img_modified
画素調整系
- tf.image.random_contrast(image, lower, upper)で0~1で上限下限を設定してコントラスト調整
- tf.image.random_brightness(image, max_delta)で輝度値デルタの絶対値を指定して輝度調整
- tf.image.random_hue(image, max_delta=0.1)で色相δの絶対値を指定して色相調整
データMix
- 2つの学習データを混合(ラベル/データ双方を線形補完)させる 参考資料: “mixup: Beyond Empirical Risk Minimization”
- β分布に従って混合割合を調整する
def sample_beta_distribution(size, concentration_0, concentration_1):
gamma_1_sample = tf.random.gamma(shape=[size], alpha=concentration_1)
gamma_2_sample = tf.random.gamma(shape=[size], alpha=concentration_0)
return gamma_1_sample / (gamma_1_sample + gamma_2_sample)
def mix_up(ds_one, ds_two, alpha=0.4):
# ds_oneとds_twoは10枚分ずれたmnistのデータセット。
# どちらのデータセットにも入力データの画像とラベルが含まれている。
images_one, labels_one = ds_one
images_two, labels_two = ds_two
# この後の処理で必要なため、データセットのバッチサイズを取得
batch_size = tf.shape(images_one)[0]
# 上で定義したベータ分布に基づくサンプリングで、バッチサイズ分の混合割合を取得。
l = sample_beta_distribution(batch_size, alpha, alpha)
x_l = tf.reshape(l, (batch_size, 1, 1, 1))
y_l = tf.reshape(l, (batch_size, 1))
# 2つのデータセットを混合割合に基づいて、入力データ・ラベルの両方を混合する。
images = images_one * x_l + images_two * (1 - x_l)
labels = labels_one * y_l + labels_two * (1 - y_l)
return (images, labels)
フレームワーク演習:Activate-Functions
実装方法
tf.keras.layers.Activationから活性化関数を指定する。
活性化関数の種類と使い道
中間層
- シグモイド関数:導関数が元の関数を用いて簡単に表現できるため、誤差逆伝播法の黎明期に使われたが、導関数の最大値が0.25で入力が0から遠ざかるほど0に近い微分値を取るため勾配消失を起こしやすい問題がある
- tanh(双曲線正接関数):導関数の最大値は1であり、シグモイドよりは勾配消失を起こしづらいが、入力が0から遠ざかるほど0に近い微分値を取るため、勾配消失問題は依然として残る。入力==0で微分不可能
- ReLU(正規化線形関数、ランプ関数):入力値が正のとき、微分値が常に1のため、勾配消失は起こりにくい、入力が負のときは微分値が常に0のため学習が進まない問題がある、入力==0で微分不可能
- Leaky ReLU:ReLUの入力が負のときに学習が進まない問題に対応するために、入力が負の領域にも小さな傾きを与える。
- Swish(シグモイド加重線形関数):入力==0の点で連続で、微分不可能な点が存在しない。シグモイドと入力の積で表され、正の領域の大半で微分値が1程度であり、勾配消失も起こしにくい
出力層
- シグモイド関数:二値分類
- ソフトマックス関数:多クラス分類
- 恒等関数:回帰タスク (出力層で、このあと層を重ねるわけでは無いため線形関数でも問題無い)
考察+α
活性化関数に関するサーベイ論文より
重要な要素
- Must
- 微分可能:誤差逆伝播が出来なくなる
- 非線形:線形だと層を深くする意味がなくなる
- Better
- 勾配消失しない:層を深くしたときの学習がすすまなくなる
- 計算効率
経験則
2021年サーベイ論文(Activation Functions in Deep Learning: A Comprehensive Survey and Benchmark)
- シグモイド関数と tanh は、畳み込みニューラルネットワーク (CNN) には使わない
- ReLU がデフォルトの選択肢になっているが、Swish, Mish, PAU (Molina et al., 2019) などは問題によって検討の価値がある
- ReLU, Mish, PDELU は VGG16 と GoogLeNet に、ReLU, LReLU, ELU, GELU, CELU, PDELU は、ResNet など残差接続を持つモデルに向いている
- PAU のようなパラメトリックな活性化関数は、より良い収束性能を示す
- tanh と SELU は言語翻訳タスクに適している
- PReLU, GELU, Swish, Mish, PAU は、音声認識モデルに適している
- トランスフォーマーでは、GELU に加え、Squared ReLU や、GLU の変種 (ReGLU, GEGLU, SwiGLU) を試す
ReLU
GELU
Gaussian Error Linear Unit 確率的正則化を取り入れた活性化関数。 入力がちいさくなるほど、値が0にドロップされる確率が高くなる。 入力を正規分布と仮定し、その累積分布関数$\phi(x)$の大きさによってマスクを0,1にする。 これを確率的でなく決定的に扱うために期待値を取って、 $f(x) = x\phi(x)$
有効だったタスク
- 画像分類 及び そのオートエンコーダー
- 品詞分析
- 音素認識
GLU
ゲート付き線形ユニット 非線形活性化関数の出力に、同じ入力を持つ線形変換の出力の要素積を取る ${\rm GLU}(x) = \sigma(xW + b) \otimes (xV + c)$
確認問題
CNNの復習

RNNの3つの重みについて
 一つ前の入力データに対する中間層出力を今回の中間層に入力する際にかけられる重み。
一つ前の入力データに対する中間層出力を今回の中間層に入力する際にかけられる重み。
RNNでの演習チャレンジ
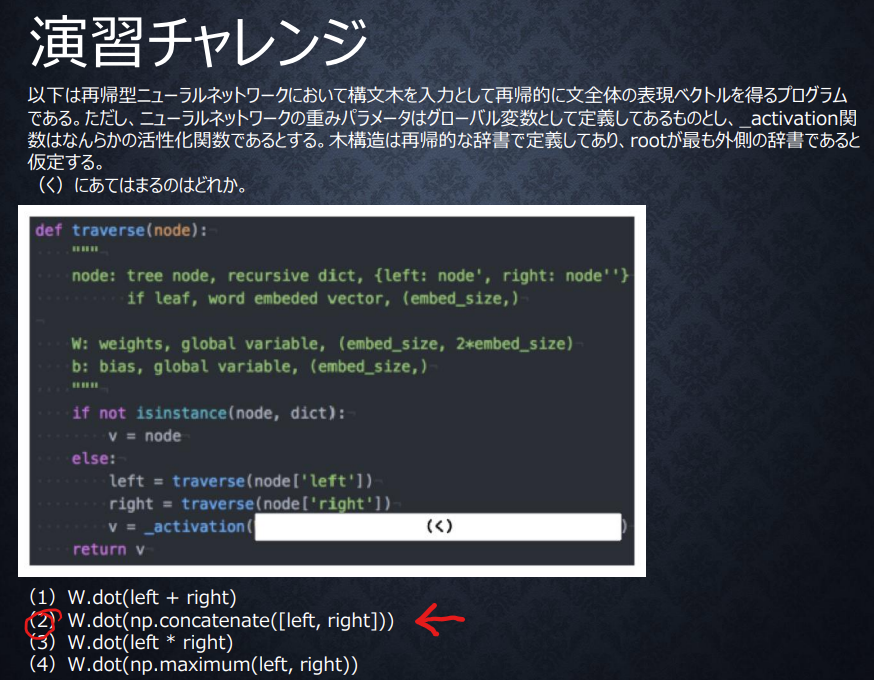 隣接単語から表現ベクトルを作る処理は隣接しているLeftとRightに重みをかけ合わせることでできる。
(1)では隣接単語が修飾、被修飾のような関係なら可能性はあるが、その場合も足し合わせた言葉が埋め込めるだけのベクトル空間が必要になり、あまり良くはないと考えられる
(2)は各入寮単語のベクトル構造が保持され、順序情報も残るのでこれが望ましいと考えられる
(3)では2つの単語の同一度に対して重みをかけている処理になり、求めていることはできない
(4)では完全によくわからないベクトルを生み出すことになるため、求めていることはできない
隣接単語から表現ベクトルを作る処理は隣接しているLeftとRightに重みをかけ合わせることでできる。
(1)では隣接単語が修飾、被修飾のような関係なら可能性はあるが、その場合も足し合わせた言葉が埋め込めるだけのベクトル空間が必要になり、あまり良くはないと考えられる
(2)は各入寮単語のベクトル構造が保持され、順序情報も残るのでこれが望ましいと考えられる
(3)では2つの単語の同一度に対して重みをかけている処理になり、求めていることはできない
(4)では完全によくわからないベクトルを生み出すことになるため、求めていることはできない
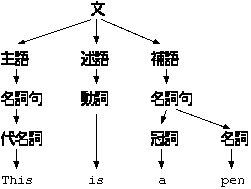 (Content Free Grammer and Syntax Treeより引用)
(Content Free Grammer and Syntax Treeより引用)
連鎖律の計算の復習

BPTTの数学的記述の確認
 $y_1 = g(W_{out}\cdot z_1 + c)$
※$z_1 = f(W_{in} \cdot x_0 + W \cdot z_0 +b)$
$y_1 = g(W_{out}\cdot z_1 + c)$
※$z_1 = f(W_{in} \cdot x_0 + W \cdot z_0 +b)$
BPTTの実装確認問題
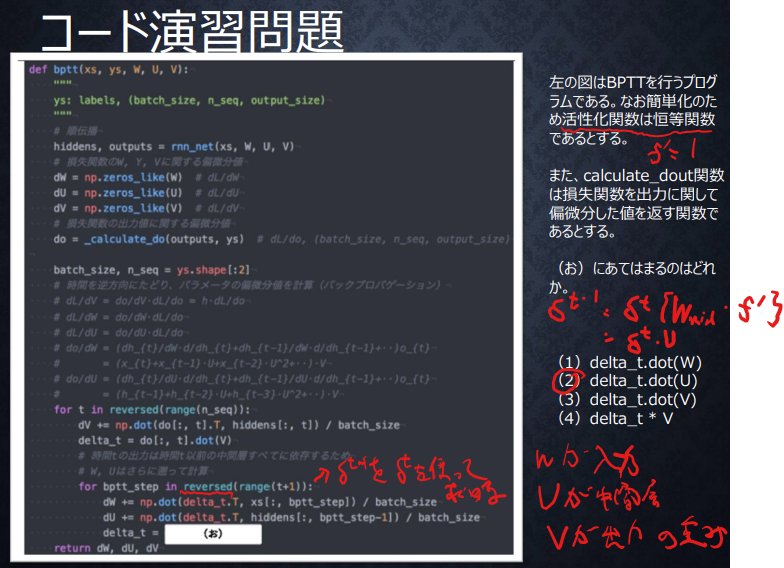 答えは(2)、
一つ前のdelta_tを求めるため、講義スライド中の下図の式が参考になる。
文字の対応が異なっているのでややこしいが、コード中のWが入力、Uが中間層(式中の無印Wと対応)、Vが出力層の重みであることがわかるので、活性化関数が恒等写像でf’が1であることをあわせて、(2)が正解となる。
答えは(2)、
一つ前のdelta_tを求めるため、講義スライド中の下図の式が参考になる。
文字の対応が異なっているのでややこしいが、コード中のWが入力、Uが中間層(式中の無印Wと対応)、Vが出力層の重みであることがわかるので、活性化関数が恒等写像でf’が1であることをあわせて、(2)が正解となる。

勾配消失問題 シグモイド関数の微分値
 答えは(2)
答えは(2)
勾配クリッピングの演習チャレンジ
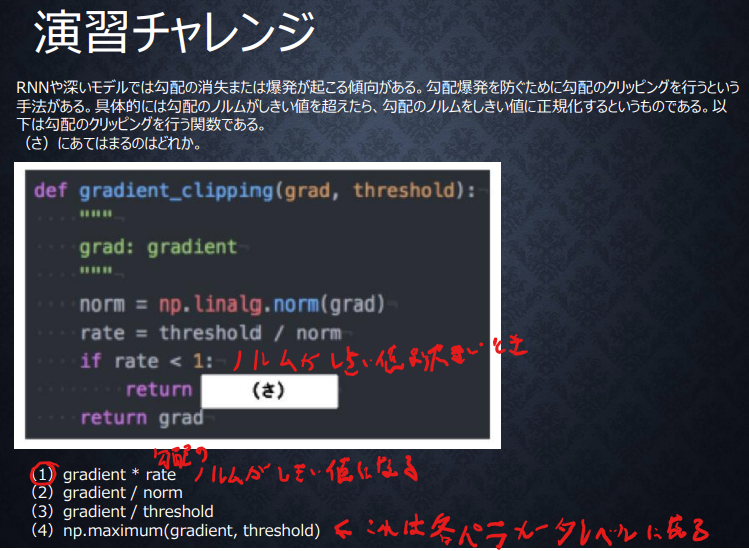 答えは(1),
クリッピングなので、値が大きいときだけしきい値でキャップをすればよく、rate<1の条件がついている。
もともとnormサイズのベクトルなので、rateをかければthresholdのサイズになる。
答えは(1),
クリッピングなので、値が大きいときだけしきい値でキャップをすればよく、rate<1の条件がついている。
もともとnormサイズのベクトルなので、rateをかければthresholdのサイズになる。
各ゲートの役割の確認問題
 不要な過去情報を削除するので、忘却ゲート
不要な過去情報を削除するので、忘却ゲート
LSTMの順伝播の演算の確認
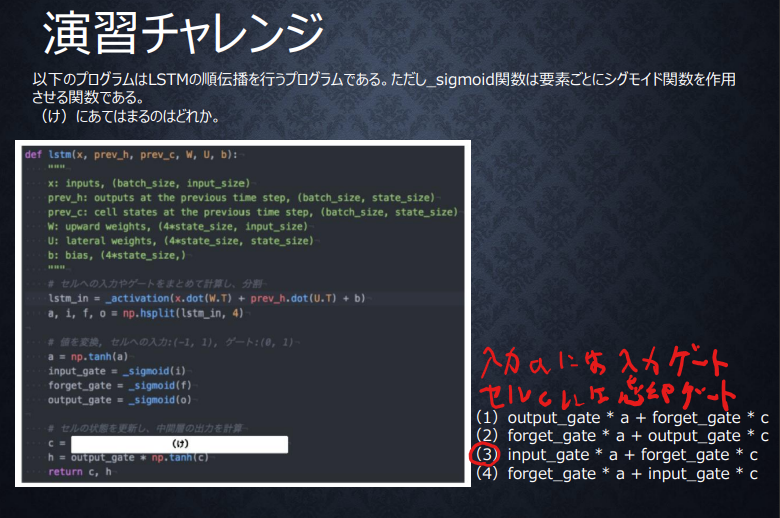 新しいセルの状態は、セルへの入力とワンステップ前のセルの状態に忘却ゲートを適用したものの和になるので(3)が正解。
新しいセルの状態は、セルへの入力とワンステップ前のセルの状態に忘却ゲートを適用したものの和になるので(3)が正解。
LSTMとCECの問題点
 LSTM:計算パラメータが多く、効率が悪い
CEC:学習ができない
LSTM:計算パラメータが多く、効率が悪い
CEC:学習ができない
GRUの更新ゲートの演習問題
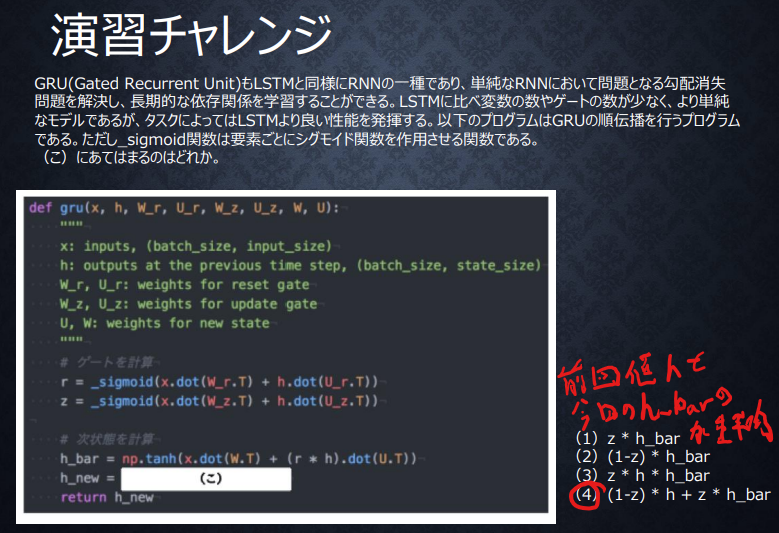
LSTMとGRUの違い
 計算量がLSTM>GRUで、
LSTMが隠れ層とCECの2つのメモリ構造で長期短期記憶を表現していたのに対して、GRUは更新制御によって隠れ層のみで長期短期記憶を表現している。
計算量がLSTM>GRUで、
LSTMが隠れ層とCECの2つのメモリ構造で長期短期記憶を表現していたのに対して、GRUは更新制御によって隠れ層のみで長期短期記憶を表現している。
双方向RNNの実装
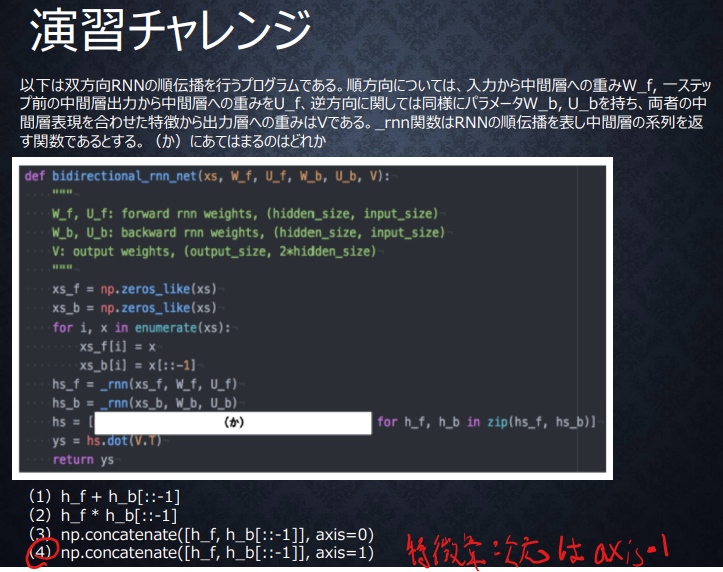 入力xsのforwardとbackwardからaxis=0が時系列方向であることがわかる。
中間層表現を合わせた特徴とあるので、特徴量の方向でconcatenateした(4)が正解。
入力xsのforwardとbackwardからaxis=0が時系列方向であることがわかる。
中間層表現を合わせた特徴とあるので、特徴量の方向でconcatenateした(4)が正解。
Seq2Seqの確認
 正解は(2)
(1):双方向RNNの説明
(3):木構造RNNの説明:ゲート機構を木構造に拡張したもの
(4):LSTM
正解は(2)
(1):双方向RNNの説明
(3):木構造RNNの説明:ゲート機構を木構造に拡張したもの
(4):LSTM
Embeddingの実装の確認
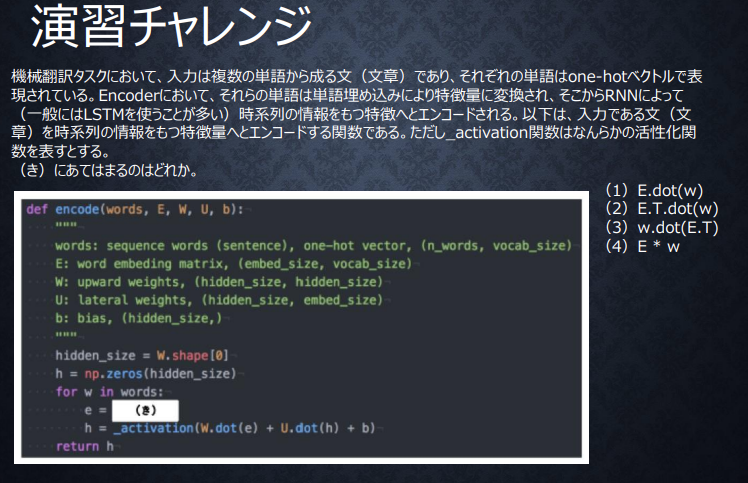 eとしてembed_sizeの長さのベクトルがほしいので、正解は(1)
※図中はWとUのサイズが逆になっていると思われる。
eとしてembed_sizeの長さのベクトルがほしいので、正解は(1)
※図中はWとUのサイズが逆になっていると思われる。
Seq2SeqとHRED,VHREDの違い
 Seq2Seqは文に対して文を回答する形で、前後の文の系列を加味して文脈を理解することはできない
HREDはSeq2SeqにContext-RNNを組み合わせることで、前後の文の系列を加味して文脈を理解して回答することができるが、生成される回答について話の展開というレベルでの多様性が無いことや、短く情報量の少ない回答を選びがちという問題がある
VHREDはHREDの上記の問題に対応するためにVAEの潜在変数の概念を取り込んで回答に多様性が生まれる様にしたものである。
Seq2Seqは文に対して文を回答する形で、前後の文の系列を加味して文脈を理解することはできない
HREDはSeq2SeqにContext-RNNを組み合わせることで、前後の文の系列を加味して文脈を理解して回答することができるが、生成される回答について話の展開というレベルでの多様性が無いことや、短く情報量の少ない回答を選びがちという問題がある
VHREDはHREDの上記の問題に対応するためにVAEの潜在変数の概念を取り込んで回答に多様性が生まれる様にしたものである。
VAE
 確率変数
確率変数
用語の違いの説明
 RNNは時系列データを処理するのに適したNNモデルのこと
Seq2Seqは入力系列に対して出力も系列でだすNN
Word2Vecは自然言語処理において単語を効率的にベクトルに埋め込む分散表現を得る手法
Attentionは時系列データの入出力の関連度合いに応じて重みをつける手法
RNNは時系列データを処理するのに適したNNモデルのこと
Seq2Seqは入力系列に対して出力も系列でだすNN
Word2Vecは自然言語処理において単語を効率的にベクトルに埋め込む分散表現を得る手法
Attentionは時系列データの入出力の関連度合いに応じて重みをつける手法
実装演習結果
3_1_simple_RNN_after.ipynb
| パラメータ変更 | 重み初期化の変更 | 活性化関数の変更 |
|---|---|---|
(ベースライン)隠れ層のノード数=16分散1の正規分布で重みを初期化sigmoid関数を使用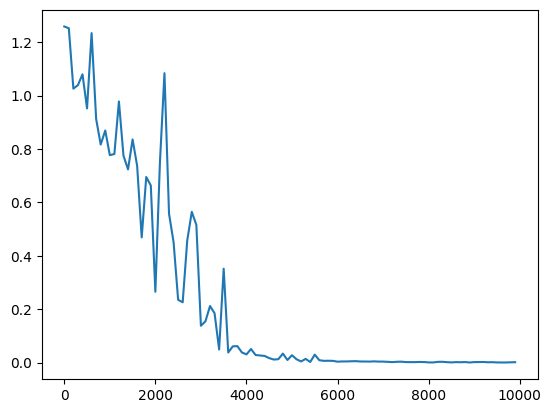 Leraning_rateを0.1→0.01に変更※小さすぎたためか収束まで至らず Leraning_rateを0.1→0.01に変更※小さすぎたためか収束まで至らず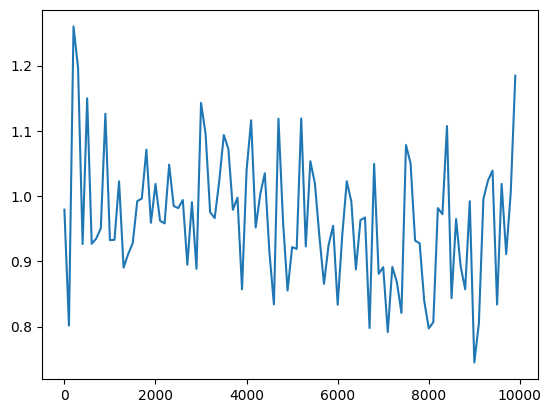 重み初期値の分散を0.2に変更/2.0に変更 重み初期値の分散を0.2に変更/2.0に変更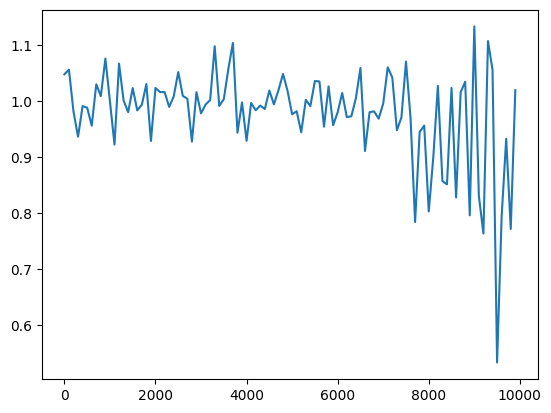 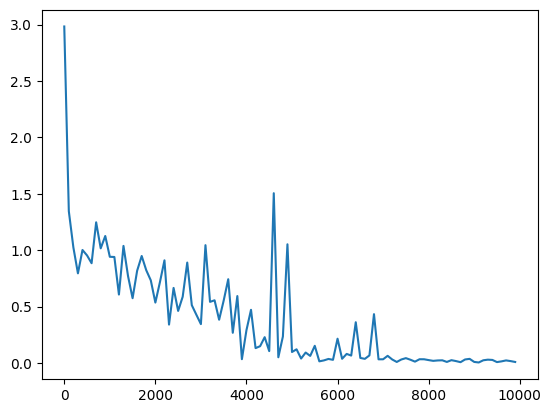 隠れ層のノード数を128に変更 隠れ層のノード数を128に変更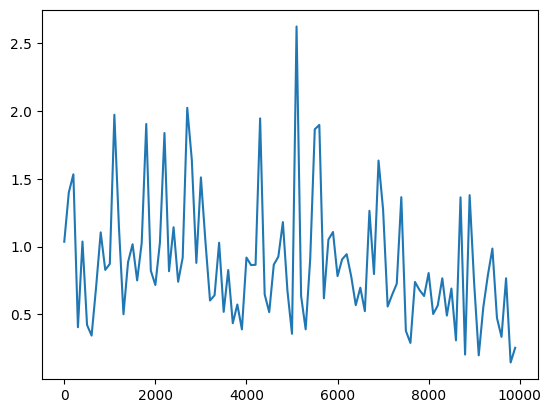 |
Xavierの初期化 (簡略版)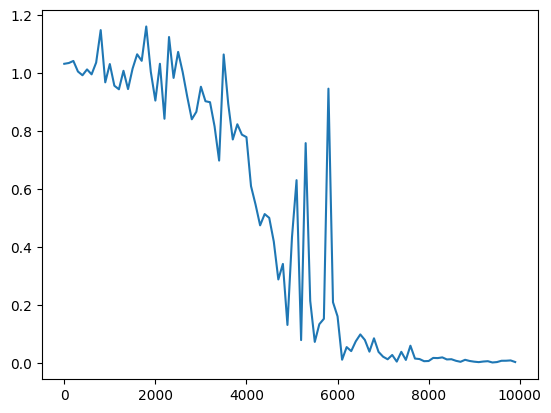 Heの初期化 Heの初期化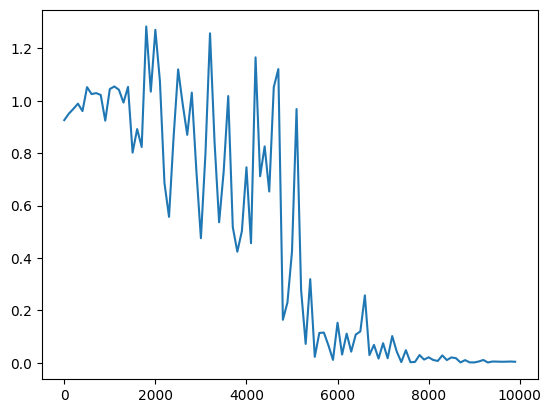 Xavierの初期化(中間層のノード数を128にしたとき) Xavierの初期化(中間層のノード数を128にしたとき)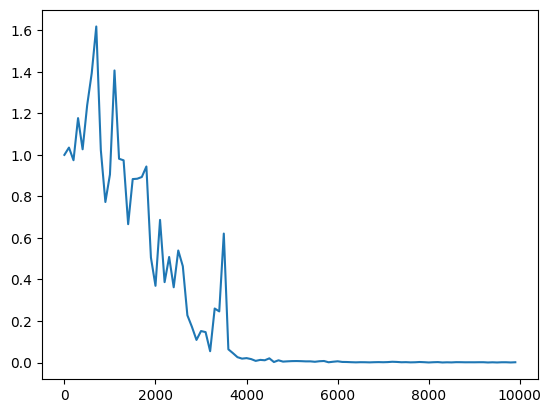 |
ReLU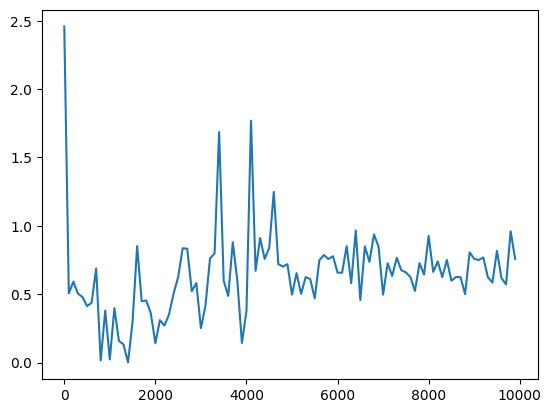 tanh関数 tanh関数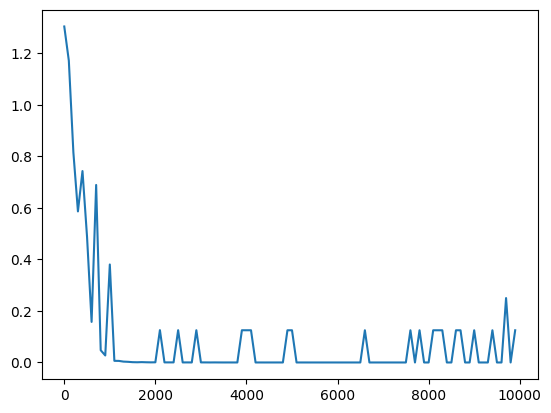 |
考察
今回のケースにおいては、入力値をスケーリングしていないため、ReLU関数を中間層の活性化関数に用いると入力が大きい値のときに誤差逆伝播で中間層出力→W_inに戻すときの$\frac{du}{dw}\cdot\frac{df(u)}{du}$が入力値になるために大きくなる。このことから重みの収束が悪くなる。 sigmoidやtanhを使った場合は0から離れると導関数の値が0に近づいていくため、収束性は良くなったものと考えられる。
重み初期値の分散を小さくしすぎるとほとんど同じ値のまま学習がうまく行かない。
隠れ層のノード数を128にしたときに収束が悪くなったのは、重み初期化の観点だと、初期値を与える分布の分散の値がXavierの初期化の厳密なバージョン($\frac{2}{n_{in}+n_{out}}$)から考えると大きくなりすぎたためだと考えられる。
hidden_layer_size = 16のとき、厳密なXavierだと1/3倍、hidden_layer_size=128のときだとおよそ1/8倍する必要があるが、等倍だったため分散が大きくなりすぎたものと考えられる。
実際単純にinit_std=0.25にして、すべての層の重みの初期化分布の分散を一括で小さくしても収束していく傾向は見られた。
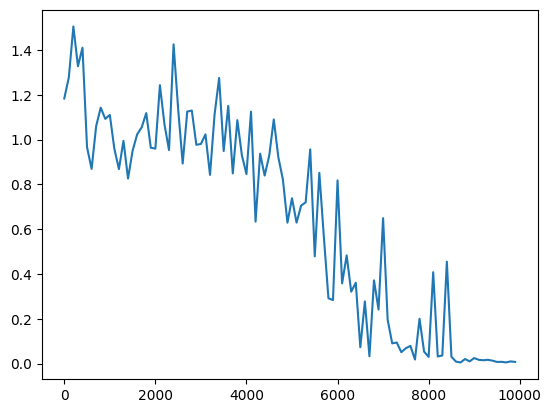
考察+α 参考図書など
He et al., 2015. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification より、重みの初期化による学習の違いは層が深くなるに連れて顕著になる。
3_4_spoken_digit.ipynb (双方向RNNと勾配クリッピング)
tf.keras.layers.Bidirectional を用いて双方向LSTMを実装
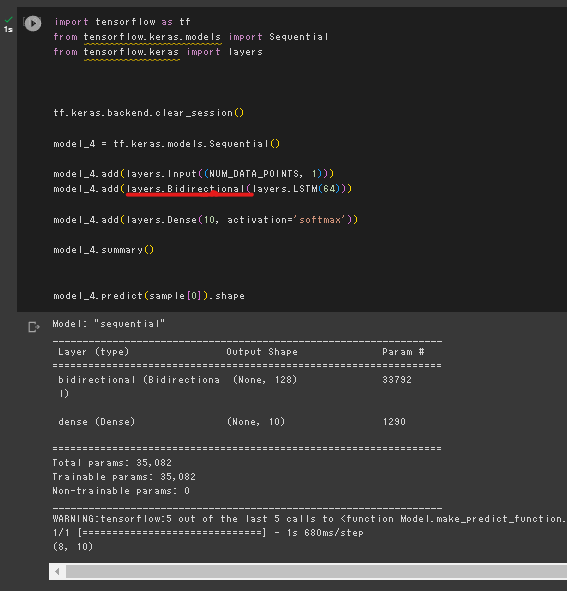 modelインスタンスのコンパイルメソッド実行時の引数として渡すオプティマイザーにclipvalueを引数として設定することで勾配クリッピングを実装
modelインスタンスのコンパイルメソッド実行時の引数として渡すオプティマイザーにclipvalueを引数として設定することで勾配クリッピングを実装
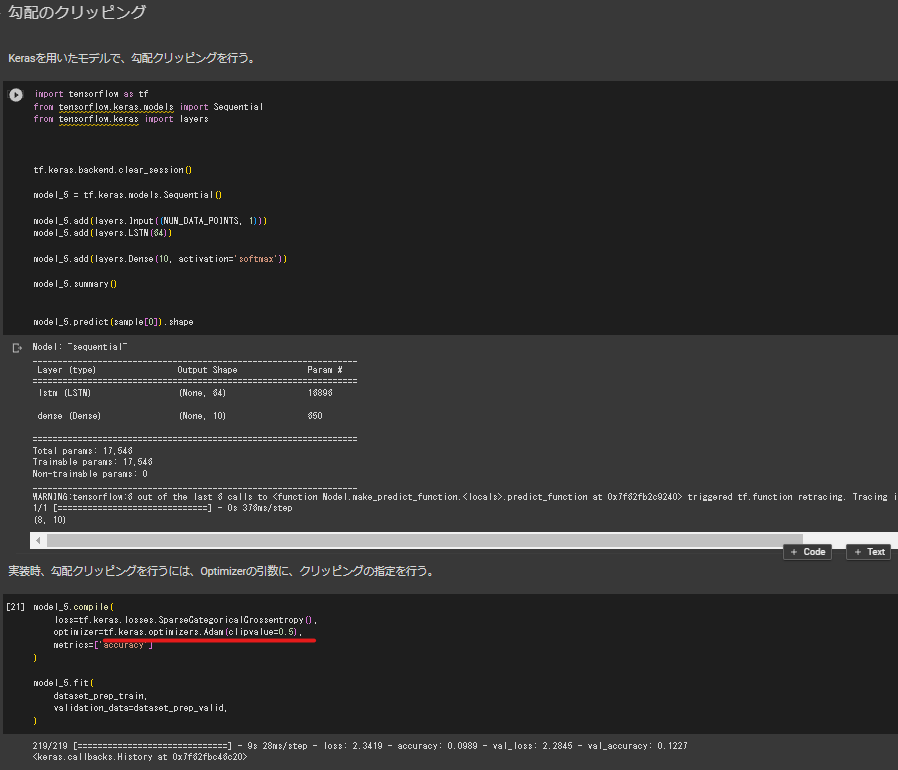
3_5_Seq2Seq(Encoder-Decoder)_sin-cos.ipynb
訓練
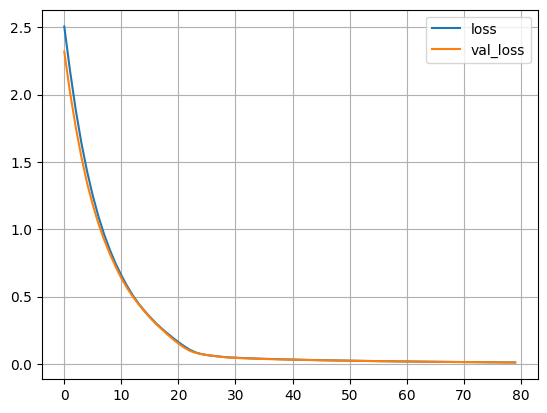
推論
sin関数かcos関数を予想
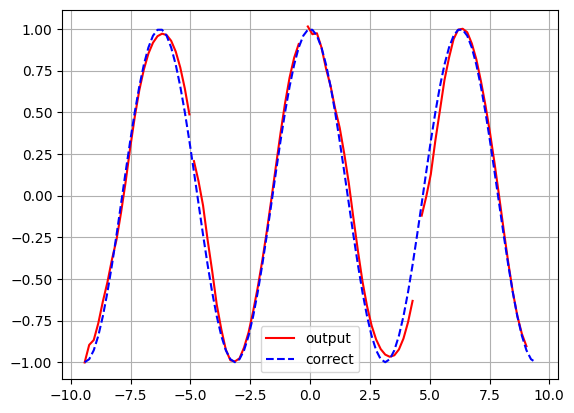
3_6_data_augmentation_with_tf.ipynb
元画像 |
左右反転 |
上下反転 |
Hue |
コントラスト |
輝度 |
回転 |
random erase

mix up

複数手法を組み合わせて実施

3_7_activation_functions.ipynb
シグモイド関数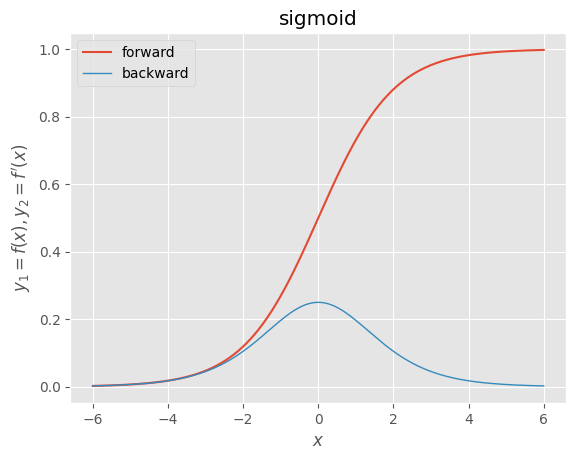 |
tanh関数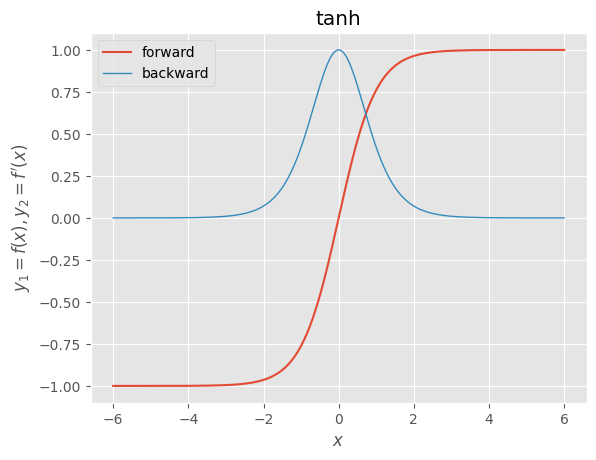 |
ReLU 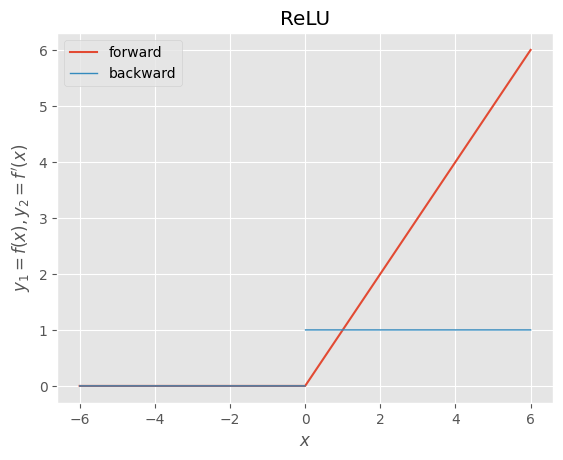 |
Leaky ReLU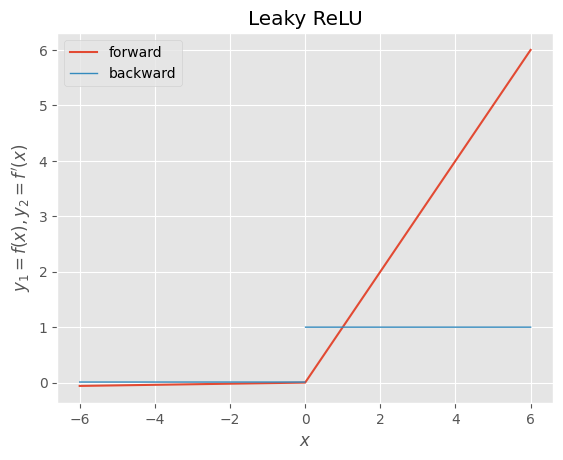 |
Swish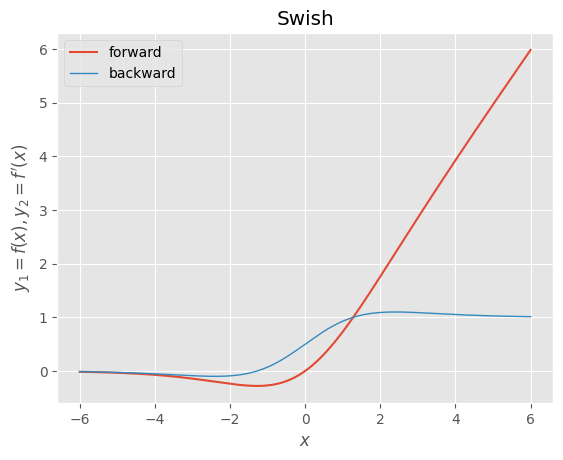 |
ソフトマックス関数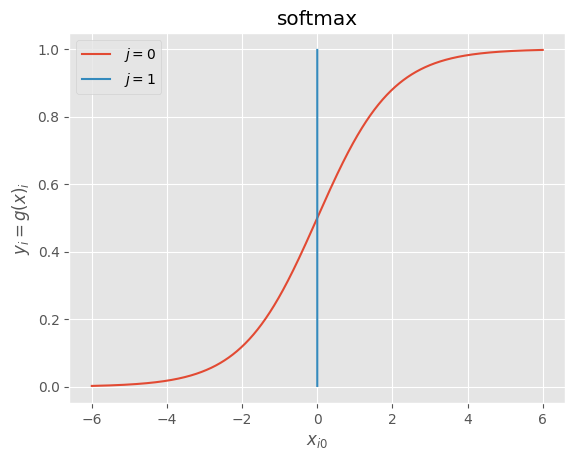 |
