DeepLearningDay4
実施内容と得点表
| 章タイトル | 要点 | 実装演習 | 確認テストまたは考察 | 参考図書など関連記事レポート |
|---|---|---|---|---|
| 強化学習 | ◯ | ◯ | ||
| AlphaGo | ◯ | ◯ | ||
| 軽量化・高速化技術 | ◯ | ◯ | ||
| 応用技術 | ◯ | ◯ | ◯ | |
| ResNet | ◯ | ◯ | ◯ | |
| EfficientNet | ◯ | - | - | ◯ |
| 物体検知と SS 解説 | ◯ | - | - | ◯ |
| Mask R-CNN | ◯ | - | - | ◯ |
| FCOS | ◯ | - | - | ◯ |
| Transformer | ◯ | - | - | ◯ |
| BERT | ◯ | ◯ | ◯ | ◯ |
| GPT | ◯ | - | - | ◯ |
| 音声認識 | ◯ | - | - | ◯ |
| CTC | ◯ | - | - | |
| DCGAN | ◯ | - | - | ◯ |
| Conditinal GAN | ◯ | - | - | ◯ |
| Pix2Pix | ◯ | - | - | ◯ |
| A3C | ◯ | - | - | |
| Metric-Learning | ◯ | - | - | |
| MAML | ◯ | - | - | |
| GCN | ◯ | - | - | ◯ |
| CAM,Grad-CAM,LIME,SHAP | ◯ | ◯ | - | |
| Docker | ◯ | - | - |
合計:45 基準:36
要点
強化学習
強化学習とは
環境の中で長期的に報酬を最大化できるように、行動を選択できるエージェントを作ることを目標とする機械学習の一分野
→ 行動の結果から与えられる報酬をもとに行動を決定する原理を改善していく仕組み
マーケティングでの応用例
- エージェント
- 入力:プロフィールと購入履歴
- 行動:顧客ごとにキャンペーンメールを送る、または送らない
- 報酬:キャンペーンのコスト、キャンペーンで生み出されると推測される売上
- 環境:会社の販売促進部(+顧客)
探索と利用のトレードオフ
環境について事前に完璧な知識がある状態(行動と報酬の関係が既知)なら最適な行動を決定することは可能
ただし、強化学習は上記仮定が成り立たないケースで適用する →不完全な知識をもとに行動しながらデータを収集して最適な行動を見つけていく
持っている知識の範囲でベストな行動を取り続ける(利用)とより良い結果は見つけ出せないが、 未知の行動(探索)のみを取り続けると過去の経験が活かせない
強化学習のイメージ
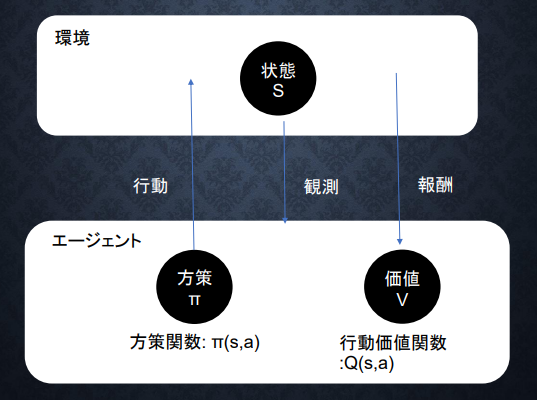 (強化学習のイメージ:講義スライドより引用)
(強化学習のイメージ:講義スライドより引用)
強化学習とその他の機械学習手法の違い
目標が異なる
- 教師あり・教師なし学習:データに含まれるパターンの抽出
- 強化学習:優れた方策の発見
主な手法
- Q 学習:行動価値関数を行動するごとに更新することにより学習を進める手法
- 関数近似法:価値関数や方策関数を関数近似する手法のこと
価値関数
- 状態価値関数
- 行動価値関数
- 平均報酬
- 割引報酬
方策関数
状態にもとづいてどのような行動を取るのかの確率を与える関数
方策勾配法
方策をモデル化して最適化する手法
方策の良さ (価値関数) を J として、方策関数のパラメータを更新していく
$$\pi(s, a | \theta)$$
$$
\underbrace{\theta^{(t+1)}}{パラメータ} = \theta^{(t)} + \epsilon \nabla \underbrace{J(\theta)}{報酬の期待値}
$$
$$\nabla_\theta J(\theta) = \nabla_{\theta} \underbrace{\sum_{a \in A}\pi_{\theta}(a|s) Q^{\pi}(s, a)}_{報酬の期待値}$$
$$\nabla_{\theta}J(\theta) = \mathbb{E}{\pi{\theta}}[(\nabla_{\theta}log\pi_{\theta}(a|s)Q^{\pi}(s,a))]$$
参考文献レポート
黒本において、17章 深層学習を用いた強化学習が該当 強化学習において問題とされる経験の自己相関に関わる内容として、DQN における体験再生の話題が入っていた。 DQN の工夫は
- 体験再生
- データ効率向上
- 入力系列の相関を断ち切れる→更新の分散低減
- 直前んに取得したデータから受ける影響の低下→パラメータの振動低減
- 目標 Q ネットワークの固定:学習の目標値算出に用いるネットワークと行動価値推定に用いるネットワークが同一のときに学習が安定しない問題があるため、目標値算出のねとワークの固定を行い一定周期で更新するように変更した
- 報酬のクリッピング
AlphaGo
論文
-
AlphaGo (Lee) :David Silver Mastering the game of Go with deep neural networks and tree search nature 27 January 2016 “https://www.nature.com/articles/nature16961 "
-
AlphaGo Zero :David Silver Mastering the game of Go without human knowledge nature 18 October 2017 “https://www.nature.com/articles/nature16961 "
概要
Alpha Go では方策関数と価値関数を Deep Neural Network で学習する
囲碁の難しさはゲーム終了までのターンの多さ(探索の深さ)と手数の多さ(探索の幅)によるもの 探索の幅は良い方策で手数を絞り込むことで改善でき、 探索の深さは価値関数の精度を上げることで実際にゲーム終了までしなくても状態を評価できることで改善する
AlphaGo では 方策関数は Policy Net、価値関数は Value Net によって代替することでこれを実現している
- Policy Net
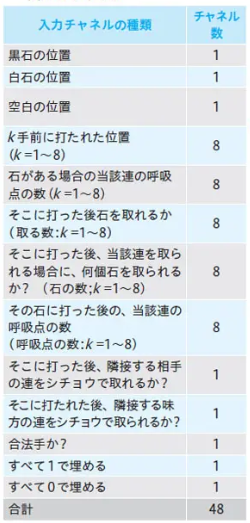
- 入力:盤面特徴入力 19✕19 の 48 チャンネル
- 出力:19✕19 マスの着手予想確率
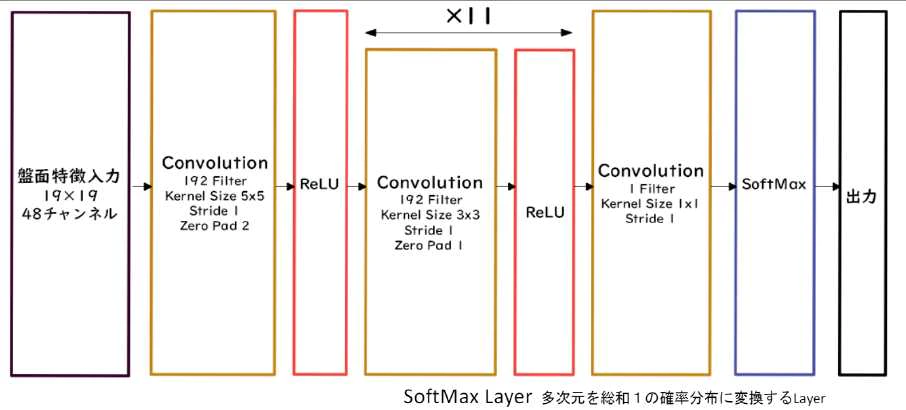 (講義スライドより引用)
(講義スライドより引用)
- Value Net
- 入力:盤面特徴入力 19✕19 の 48 チャンネル
- 出力:1~1 の範囲での現在の局面の勝率
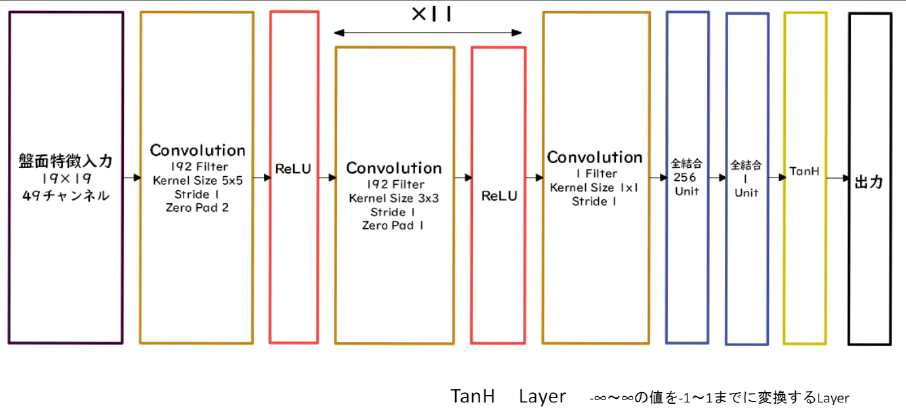 (講義スライドより引用)
(講義スライドより引用)
入力特徴量
PolicyNet と Value ネットの共通特徴量
ValueNet だけの特徴量
現在の手番が黒番であるかどうか
RollOutPolicy の特徴量
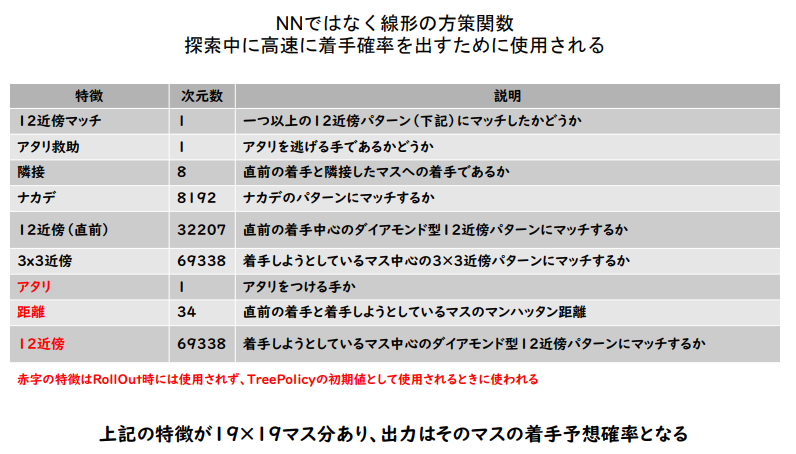 (講義スライドより引用)
(講義スライドより引用)
学習の流れ
- 教師あり学習で譜面を用いて RollOutPolicy と Policy Net の学習
- 盤面のデータを入力したらその盤面のときに実際に打たれた手の確率が最大になるような確率分布を出力するように学習させる
- 強化学習で Policy Net の学習
- 更新させる Policy Net と PolicyPool(教師あり学習で出力させた PolicyNet~これまでの強化学習で更新された PolicyNet)からランダムに選んだネットワークを戦わせる
- 強化学習で Value Net の学習
- 強化学習部分
- まず SL PolicyNet(教師あり学習で作成した PolicyNet) で N 手まで打つ。
- N+1 手目の手をランダムに選択し、その手で進めた局面を S(N+1)とする。
- S(N+1)から RL PolicyNet(強化学習で作成した PolicyNet)で終局まで打ち、その勝敗報酬を R とする。
- 強化学習させた Policy Net 同士を戦わせた盤面と勝敗を教師データとして学習させる
- 強化学習部分
モデルを用いた探索
以下の4ステップからなるモンテカルロ木探索を行う
- 選択
- 評価
- バックアップ
- 成長
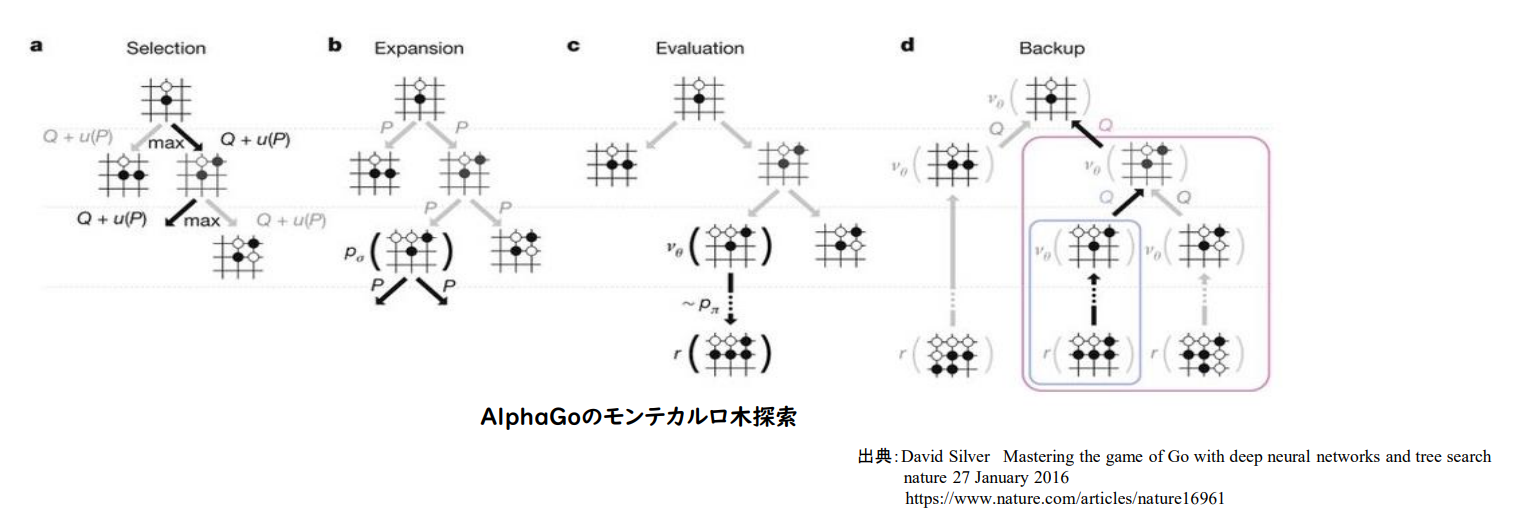 (講義スライドより引用)
(講義スライドより引用)
AlphaGoZero
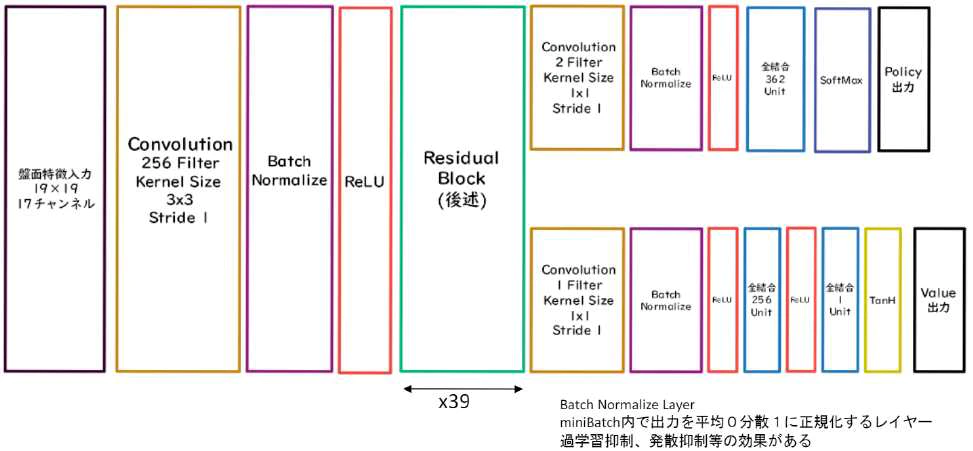 (講義スライドより引用)
(講義スライドより引用)
AlphaGoZero と AlphaGo の違い
- 教師あり学習を一切行わず、強化学習のみで作成
- 特徴入力からヒューリスティックな要素を排除し、石の配置のみにした
- PolicyNet と ValueNet を1つのネットワークに統合した
- Residual Net(後述)を導入した
- モンテカルロ木探索から RollOut シミュレーションをなくした
参考文献レポート
黒本 p366、369に該当の問題があった。 各学習ステージにおけるパラメータの勾配の式があったため、以下にまとめる。
教師有り学習による方策ネットワーク学習 (勾配上昇法)
$$ \Delta \sigma=\frac{\alpha}{m} \sum_{k=1}^m \frac{\partial \log p_\sigma\left(a^k \mid s^k\right)}{\partial \sigma}\ $$
強化学習による方策ネットワーク学習 (勾配上昇法)
$$\Delta \rho=\frac{\alpha}{n} \sum_{i=1}^n \sum_{t=1}^{T^i} \frac{\partial \log p_\rho\left(a_t^i \mid s_t^i\right)}{\partial \rho}\left(z_t^i-v\left(s_t^i\right)\right)\ $$
強化学習による価値ネットワーク学習(勾配降下法)
$$ \Delta \boldsymbol{\theta}=\frac{\alpha}{m} \sum_{k=1}^m\left(z^k-v_\theta\left(s^k\right)\right) \frac{\partial v_\theta\left(s^k\right)}{\partial \theta} $$
モンテカルロ法についても記載があったので、簡単にまとめると AlphaGo で使われるモンテカルロ木探索アルゴリズムは Asynchronous policy and Value MCTS と呼ばれる。 非同期処理だが、記録ステップの工夫で重複したシミュレーションを避けている。
行動の選択には行動価値関数と PUCT アルゴリズムに基づく、広い探索に関するボーナス項で構成される目的関数を最大化する行動が選ばれる。
行動価値関数は価値ネットワークの行動価値の総和を更新回数で割った値とロールアウトに基づく行動価値の総和を探索回数で割った値更新量の荷重平均
軽量化・高速化技術
分散深層学習
深層学習はデータ量、パラメータ更新のための計算量から高速な計算が求められる →複数の計算資源(ワーカー)を使用して並列で NN を構成することで効率のよい学習を行いたい
モデルが大きいとき→モデル並列 データが多いとき→データ並列
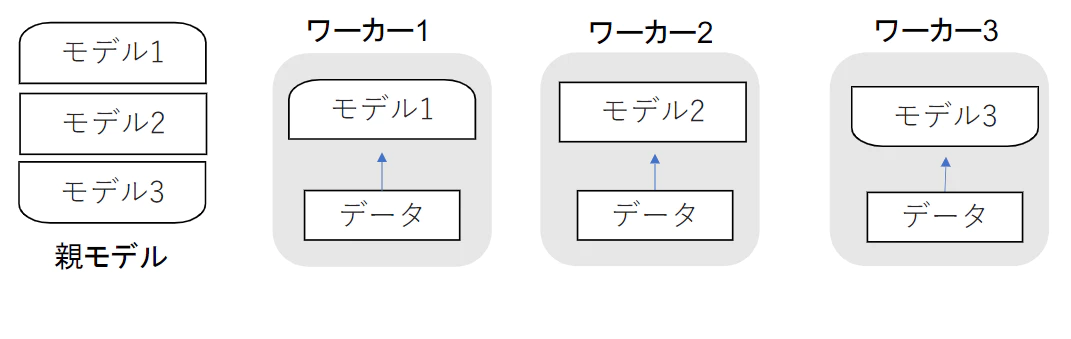
モデル並列
モデルが大きいときに利用 パラメータ数が多いほどスピードアップの効率も向上
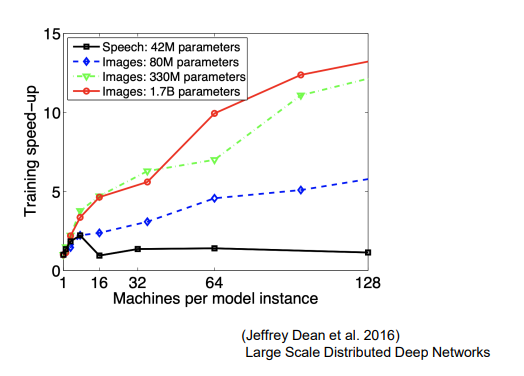 (講義スライドより引用)
(講義スライドより引用)
- 親モデルを複数の部分で分割し、各ワーカに割り当てる
- それぞれのワーカで分割したモデルを学習させる
- 学習が終わったら一つのモデルに復元
 (講義スライドより引用)
(講義スライドより引用)
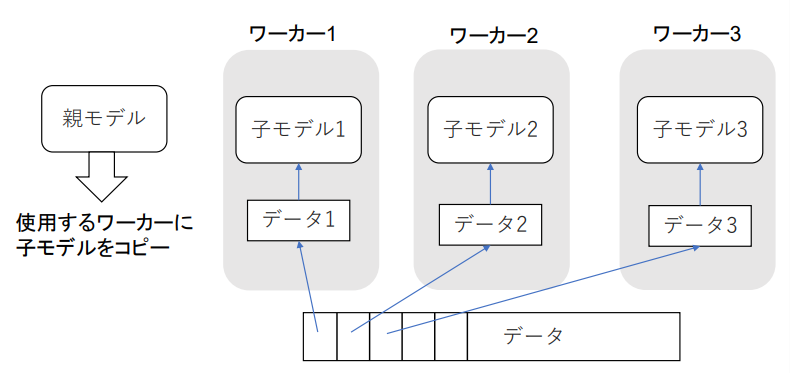
データ並列
- 親モデルを子モデルとしてコピー
- データを分割してそれぞれの子モデルに計算させる
- 同期型と非同期型の2種類
処理速度は非同期型が速いが、学習が不安定(Stale Gradient Problem)で同期型のほうが精度が良いので、同期型が主流
- 同期型:すべての子モデルの計算が終わるのを待って全ワーカーの勾配の平均をつかって親モデルの更新を行う
- 非同期型:各ワーカーごとに学習させて、学習が終わった子モデルをパラメータサーバーにキューとして Push して、新しいデータがでたらパラメータサーバから pop して学習させる
(講義スライドより引用)
GPU による高速化
GPGPU: General Purpose GPU で本来のグラフィック以外の用途で使用される GPU の総称
CPU と GPU の比較
| 種類 | コア数 | コア性能 | 特徴 |
|---|---|---|---|
| CPU | 少ない | 高性能 | 複雑で連続する処理が得意 |
| GPU | 多い | 低性能 | 簡単な並列処理が得意 |
GPGPU の開発環境
- CUDA
- GPU 上で並列コンピューティングを行うためのプラットフォーム
- NVIDIA 社が開発している GPU のみで使用可能
- Deep Leaning 用に提供されているため使いやすい
- OpenCL
- オープンな並列コンピューティングのプラットフォーム
- NVIDIA 社以外(Intel,AMD,ARM など)の GPU からでも利用可能
- DeepLearning 用の計算に特化しているわけではない
Deep Leaning 用フレームワーク内で実装されているため、使用する際にはインストールした後パスを通せば良い
モデルの軽量化
モデルの精度を保ちつつ、パラメータや演算回数を低減する手法の総称
PC に比べて性能が落ちる (主にメモリや計算速度) IoT やモバイル端末において有用な手法
量子化
変数の精度を 64bit → 32bit に落としてメモリと演算処理の削減を行う
- メリット
- 計算の高速化
- 省メモリ化
- デメリット
- 精度の低下
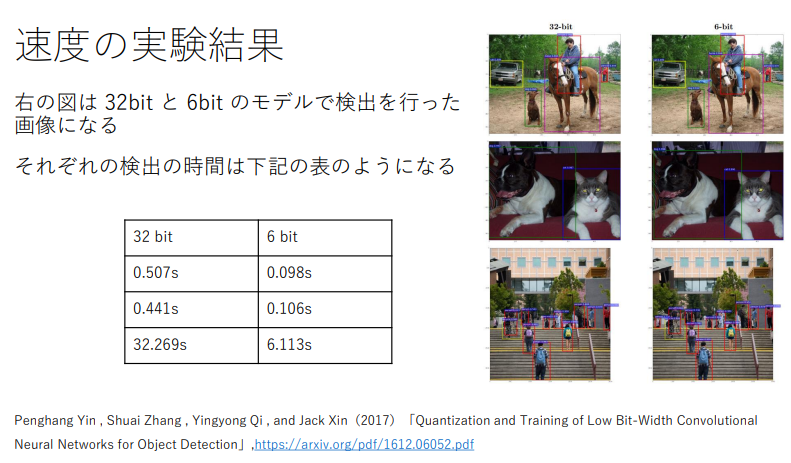
計算の高速化
処理能力を示す TeraFLOPS で評価すると、 単純に精度を半分にするとおよそ倍の処理が可能になる DeepLearning 向けの Tensor 演算もあり、そちらを利用したほうが処理能力は上がる
 (講義スライドより引用)
(講義スライドより引用)
→ TeraFLOPS の評価でも想定できたが、処理時間は精度におよそ反比例していることがわかる
省メモリ化
Float32 が使うメモリ領域は Float64 が使用するメモリ領域の半分という当たり前の話
精度の低下
Float32 にすることで有効桁数が下がるため、精度の下限以下の重みを表現できなくなる ($単精度の下限は1.175494\times10^{-38}、倍精度の下限は2.225074\times10^{-308}$)
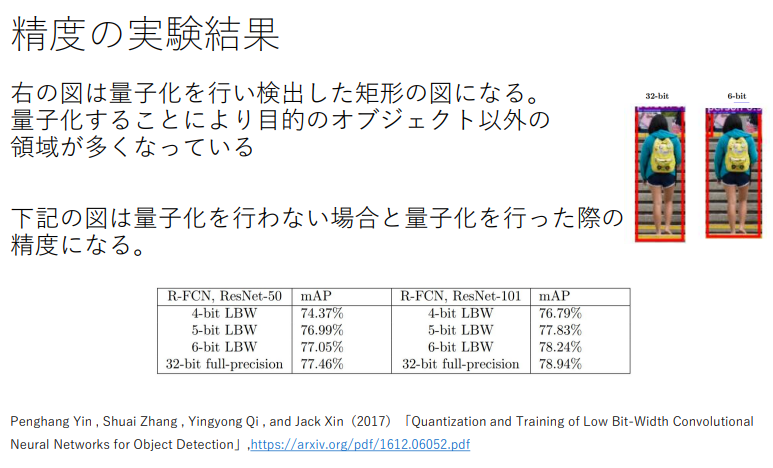
極端な量子化の例
y = 0.5 x を 1bit の精度で y = w・x で近似することを考えてみると w = {0,1} のため、
y = 0, y= x の2つしか表現できなくなり、どちらも誤差の大きい状態になってしまう。
→量子化をする際には極端に精度が落ちない程度に量子化しなくてはならない
→モデルを適用する目的(目標性能)の明確化が必要
 (講義スライドより引用)
(講義スライドより引用)
蒸留
精度が高いモデル (教師モデル) の知識を使って軽量なモデル (生徒モデル) の作成を行う
一般に
- 教師モデル:複雑なモデルや、アンサンブルを用いた高精度なモデル
- 生徒モデル:簡略化した構造を持つ軽量なモデル
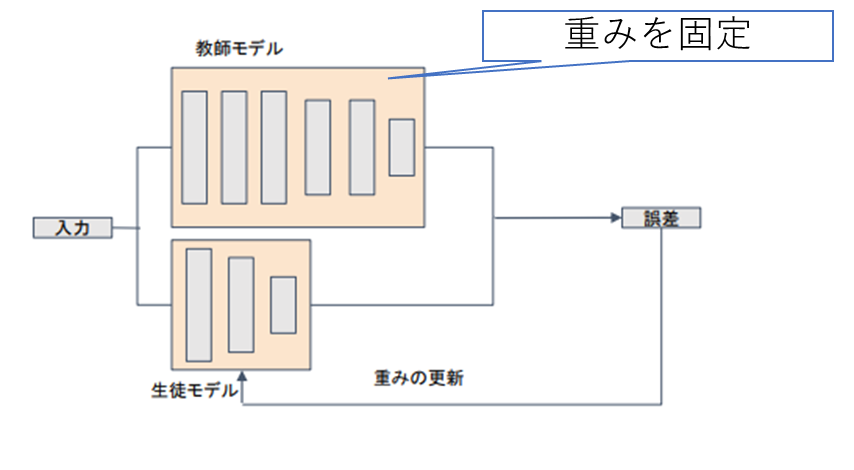 (講義スライドより引用)
(講義スライドより引用)
プルーニング
精度に寄与していないニューロンを切り落とす →モデルの軽量化、計算の高速化
重みの値によってニューロンを削減して、再学習を行う
閾値は各層の重みの標準偏差に係数をかけた値を用いて設定する
参考文献レポート
以下の図は(教師モデルはパラメータ数~9M で Multiplication~725M)演算回数を固定して、層を深くしたケースだが、通常の学習方法ではそもそも学習が進まなかったのを蒸留手法 (KD と Hint Training) では学習できていることを示している。
また、幅が広いモデルよりも深いモデルのほうが精度が高く出ていることがわかる。
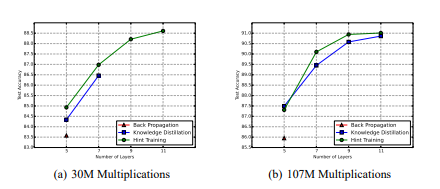 (Romero, A., Ballas, N., Kahou, S. E., Chassang, A., Gatta, C., & Bengio, Y. (2015). Fitnets: Hints for thin deep nets. In International Conference on Learning Representations.:“https://arxiv.org/pdf/1412.6550.pdf")
(Romero, A., Ballas, N., Kahou, S. E., Chassang, A., Gatta, C., & Bengio, Y. (2015). Fitnets: Hints for thin deep nets. In International Conference on Learning Representations.:“https://arxiv.org/pdf/1412.6550.pdf")
Hint Training と Knowledge Distillation の違いは以下の表
| 項目 | Hint Training | Knowledge Distillation |
|---|---|---|
| 目的変数 | 教師モデルの隠れ層からの中間レベルのヒントを使用して、生徒モデルをトレーニングする | 教師モデルの出力を使用して、生徒モデルをトレーニングする |
| 最適化方法 | 生徒モデルは、教師モデルの隠れ層からのヒント(隠れ層の出力のこと)に近づくように損失関数を最小化する | 生徒モデルは、教師モデルの出力と真のラベルの両方に近づくように損失関数を最小化する |
| 学習の比較 | 生徒モデルは、教師モデルの隠れ層からの情報を直接学習する | 生徒モデルは、教師モデルが持つ細かい情報や構造を間接的に学習する |
モデル軽量化技術についてまとめた論文があったので、そちらの表から効果のまとめ。
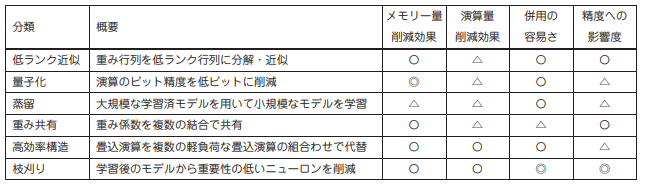 (” 山本康平 橘素子 前野 蔵人 ディープラーニングのモデル軽量化 技術 " より引用 “https://www.oki.com/jp/otr/2019/n233/pdf/otr233_r11.pdf")
(” 山本康平 橘素子 前野 蔵人 ディープラーニングのモデル軽量化 技術 " より引用 “https://www.oki.com/jp/otr/2019/n233/pdf/otr233_r11.pdf")
応用技術
MobileNet
目的
組み込みアプリケーションの実行環境で実行可能なモデルをめざして ディープラーニングモデルの軽量化・高速化・高精度化を行う
手法
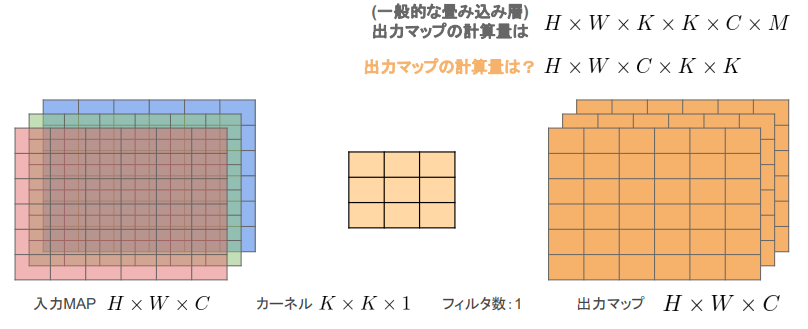
Depthwise Convolution(K✕K✕1 のカーネルをそれぞれのチャンネルに畳み込む) と Pointwise Covolution(1✕1✕C のカーネルを M 個)による軽量化 通常の CNN の計算では空間方向とチャンネル方法の畳み込みを同時に行っていたのを個別に行っている
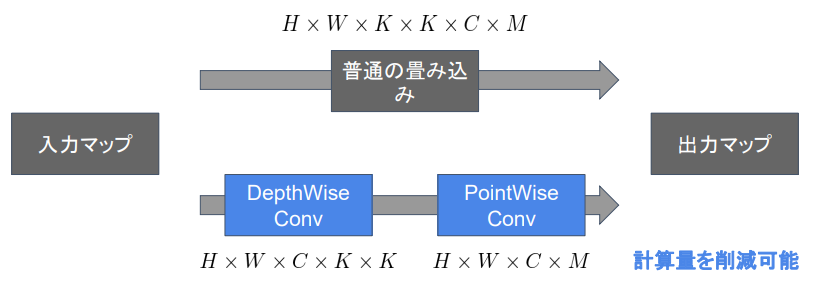 (講義スライドより引用)
(講義スライドより引用)
Depthwise Convolution
- 入力の チャンネルごと に畳み込み
- 出力マップはチャンネルごとの出力を結合
- K✕K✕1 のカーネル
※チャンネルごとで畳みこみをしているため、チャンネル方向の関係性が考慮されない問題がある。 → Pointwise Convolution をセット使うことで対応
 (講義スライドより引用)
(講義スライドより引用)
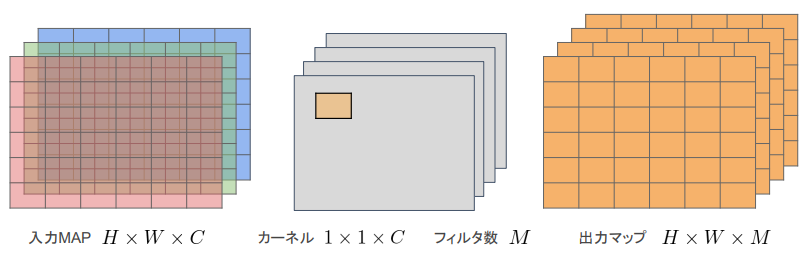
Pointwise Convolution
- 入力マップの ポイントごと に畳み込みを実施
- 出力のチャンネル数はフィルタ数で決定される
 (講義スライドより引用)
(講義スライドより引用)
DenseNet
概要
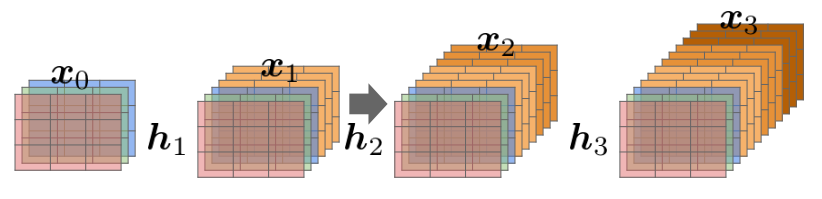
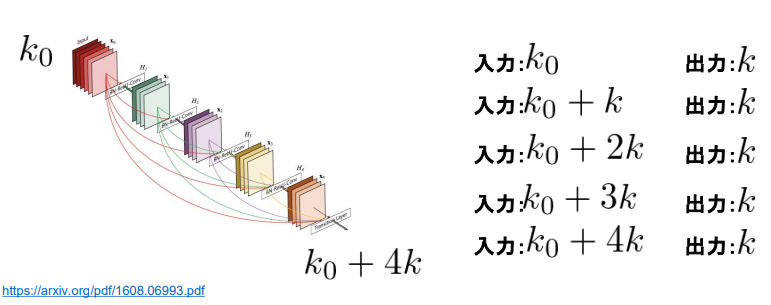
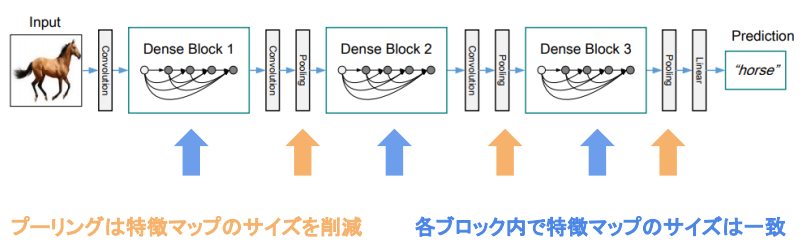
- Dense ブロック内の各層の入力はこれまでの入力すべて+直前の出力をチャンネル方向に結合したものになる
- 各層の構成は Batch 正規化→Relu→3×3× k の畳み込み
- チャンネル方向のサイズの入力は Dense ブロックに最初に入ってきたチャンネル数 $k_0$ と growth_rate:k を使って $k_0 + i \times k$ となる(i は0始まりの層のインデックス)
- Dense ブロック内で特徴マップのサイズは一定で、その間の Transition Layer(=Convolution+Pooling)でチャネルサイズと空間方向のダウンサンプリングを行う
 (講義スライドより引用)
(講義スライドより引用)
Residual ブロックとの違い
- 入力履歴の扱い
- Residual: 直前の一層の入力のみ後方の層へ入力
- Dense:ブロック内の前方の各層への入力すべてが後方の層へ入力
- ハイパーパラメータの追加:Growth_rate
Layer 正規化/Instance 正規化
2015年に提案。各層において、活性関数を掛ける前に伝播してきたデータを正規化する処理。
効果
- 学習の高速化:正規化することで極端に小さな値をクリッピングできることで、勾配消失の解決
- 初期値への依存が少なくなる
- 過学習が起こりにくい:各層の出力の正規化により、外れ値が少なくなる
- 内部共変量シフト への対応
バッチ正規化はミニバッチ単位で Normalization するのでバッチサイズが小さいときに学習が収束しない問題が起こる。 その際には Layer Normalization などを使う
正規化手法のイメージ比較
 (講義スライドより引用)
着色されてる範囲のデータを使って平均、分散を求めて正規化する。
(講義スライドより引用)
着色されてる範囲のデータを使って平均、分散を求めて正規化する。
特徴
- Batch 正規化
- 正規化の方法:空間方向とサンプル方向でデータを集計して、各チャンネルに対して正規化を適用
- Layer 正規化
- 正規化の方法:空間方向とチャンネル方向でデータを集計して、各サンプルごとに正規化を適用
- バッチ数が少なくても適用できる
- 入力データのスケールに対してロバスト
- 重み行列のスケールやシフトに対してロバスト
- Instance 正規化
- 正規化の方法:空間方向だけでデータを集計して、チャンネルとサンプルごとに正規化を適用
- コントラストの正規化に寄与する
Wavenet
概要
- 生の音声波形を生成する深層学習モデル
- Pixel CNN という高解像度の画像を精密に生成する手法を音声に応用
- Dilated Convolution をリンクを離しながら時系列データに適用→需要野の拡大 https://gigazine.net/news/20171005-wavenet-launch-in-google-assistant/ https://qiita.com/MasaEguchi/items/cd5f7e9735a120f27e2a https://www.slideshare.net/NU_I_TODALAB/wavenet-86493372
確認問題
問題 1
MobileNet のアーキテクチャ
- Depthwise Separable Convolution という手法を用いて計算量を削減し ている。通常の畳込みが空間方向とチャネル方向の計算を同時に行うの に対して、Depthwise Separable Convolution ではそれらを Depthwise Convolution と Pointwise Convolution と呼ばれる演算によって個別に行 う。
- Depthwise Convolition はチャネル毎に空間方向へ畳み込む。すなわち、 チャネル毎に $D_K×D_K$×1のサイズのフィルターをそれぞれ用いて計算を 行うため、その計算量は(い)となる。
- 次に Depthwise Convolution の出力を Pointwise Convolution によってチャネル方 向に畳み込む。すなわち、出力チャネル毎に1×1×M サイズのフィルターをそ れぞれ用いて計算を行うため、その計算量は(う)となる
回答
入出力画像の縦サイズ: H
入出力画像の横サイズ: W
フィルターのサイズ: $D_K\times D_K$
フィルタ数: M
としたとき
(い): $W\times H \times D_K \times D_K \times C$ で通常の畳み込み計算の $\frac{1}{M}$ となる
(う):$W\times H \times C\times M$ で通常の畳み込み計算の $\frac{1}{D_K\times D_K}$ となる
問題 2
深層学習を用いて結合確率を学習する際に、効率的に学習が行えるアーキテクチャを提案したことが WaveNet の大きな貢献の1つである。 提案された新しい Convolution 型アーキテクチャは(あ)と呼ばれ、結合確率を効率的に学習できるようになっている。
- Dilated Causal Convolution
- Depthwise Separable Convolution
- Pointwise Convolution
- Deconvolution
回答
1. WaveNet で提案されたのは時系列データに対して Dilated Convolution を適用すること。 2.3 は MobileNet において計算量の効率化につかわれ、4 はセグメンテーション関連で DeconvNet などで活用されるアーキテクチャ
問題 3
(あ)を用いた西尾大きな利点は単純な Convolution Layer と比べて(い)ことである。
- パラメータ数に対する受容野が広い
- 受容野あたりのパラメータ数が多い
- 学習時に並列計算が行える
- 推論時に並列計算が行える
回答
正解は1、Dilated Convolution はカーネルに隙間を空ける構造をしているので、パラメータあたりの受容野が大きくなる 2は1と逆なので✗ 学習、推論時に並列計算を行えるのは GPU を用いた CNN 共通の話で Dilated Convolution に限った話ではない。
参考文献レポート
黒本において MobileNet の問題が P232 に、DenseNet にかんする言及が P234 の問題にあった、 MobileNet に関しては計算効率化の Depthwise と Pointwise の内容が中心。 DenseNet の問題に関しては ResNet との違いで、特徴量マップを結合していくことがあげられている。
P335 に WaveNet について問題が掲載されていた。 Causal 畳み込みはモデルがデータの時間順序をやぶらないことの保証ができる。 再帰計算がない分高速 Causal 畳み込みと同等の処理にマスクテンソルと畳み込みフィルタの要素積をとってから畳み込みをおこなうマスク畳み込みがある。
ResNet
ResNet の構造
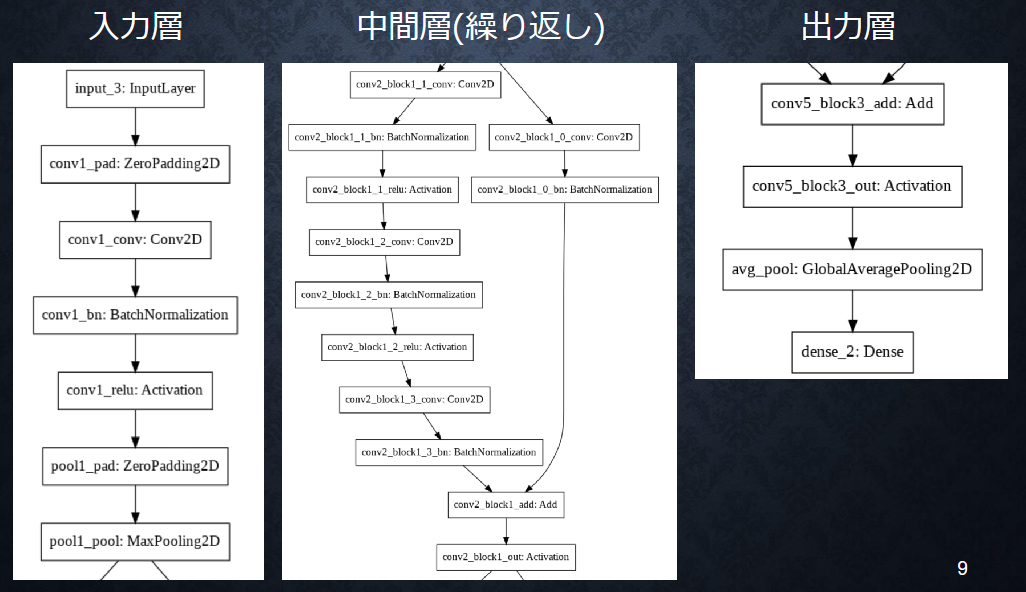
中間層の繰り返し部分では BN->ReLU->Conv が速度と精度の面で有利とのこと
 (講義スライドより引用)
(講義スライドより引用)
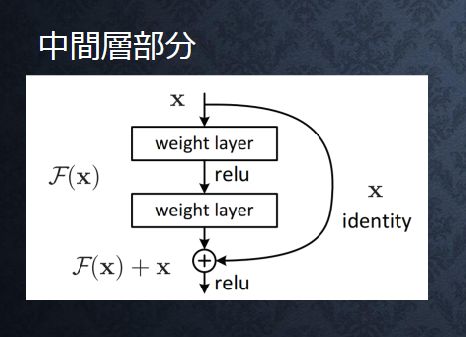
Skip Connection
 (講義スライドより引用)
(講義スライドより引用)
$$ H(x) = F(x) + x$$
※H(x) が中間層の出力、学習部分は F(x) となる
深い NN の学習を可能に - 勾配消失の回避 - 勾配爆発の回避
Bottleneck 構造
1×1 の畳み込みによる Bottleneck 構造により同一の計算コストで層数を増やした
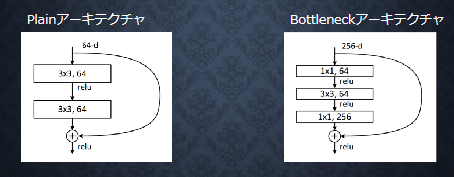 256 チャンネルを一度 64 チャンネルに落とし込むことで計算量を軽くしている
(講義スライドより引用)
256 チャンネルを一度 64 チャンネルに落とし込むことで計算量を軽くしている
(講義スライドより引用)
Wide ResNet
- 層数を浅くして、パラメータ数を増やした
- 深くする(シーケンスのステップを増やす)より広くする(並列に展開する量を増やす)方が GPU の特性に合っている⇒高速化
- Skip Connection だけでは、ブロックを強制的に経由する仕組みが無いため、無意味なブロックができてしまう
- Residual ブロックの中に DropOut を導入 パラメータを増やすことによる過学習を避けるための正則化、 原著論文内において、すでに Batch Normalization は入っているが、活用するには DataAugumentation が必要になるためそれを避けるために DropOut を導入したとある (Batch Normalization を効かせるには各チャンネル(対応特徴量)ごとのサンプル数が必要になるため、不均衡データなどを考えるとそれだけに頼らないほうがいいのでは無いかと考えられる。)
WRN-n-k : 全部で n 層の畳み込みをもち、Resnet の特徴マップのチャネル数の k 倍のチャネル数 をもつ Wide Residual Networks (パラメータの数と計算量は k の二乗になる。k=1 のとき、もとの ResNet と同じで、k>1 のとき WideResNet となる。)
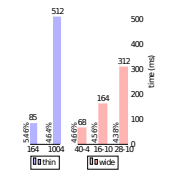 (設定別の処理時間と精度、S. Zagoruyko and N. Komodakis, “Wide Residual Networks,“https://arxiv.org/pdf/1605.07146.pdf")
(設定別の処理時間と精度、S. Zagoruyko and N. Komodakis, “Wide Residual Networks,“https://arxiv.org/pdf/1605.07146.pdf")
参考文献レポート
認定テストにおいて、パラメータ数を固定したときに、残差ブロック内の畳み込みの層数を変更したときの問題があった。 ブロック内の層数を増やすとエラー率が上がる理由は、原著論文内において、おそらく残差結合の数が減る事によって最適化が困難になったためとされ得ている。 S. Zagoruyko and N. Komodakis, “Wide Residual Networks,“https://arxiv.org/pdf/1605.07146.pdf"
EfficientNet
導入
2019 年の EfficientNet までは CNN のスケールアップで精度を改善してきたが モデルが複雑で高コストという問題があった
⇒ モデルスケーリングの法則を見つけて効率化したい ⇒ 複合係数(Conpound Coefficient)
性能
- パラメータ数、計算量は数分の1から 1/10 くらいに削減
- 同程度の計算量の ResNet-50 と比べて 6.3% 精度改善
- 転移学習で性能を発揮(過剰なパラメータがあることによる過学習が抑えられた結果、汎用性が上がったと思われる)
複合スケーリング手法
スケーラー
- Depth (d): モデルの表現力を上げる、特に次数を上げる形になるので、複雑な特徴を捉えられるようになる
- Width (w、チャンネル): 細かい特徴表現を学習、深さ対比で幅が広すぎると高レベルな特徴量を学習しにくくなる
- Resolution (r、幅・高さ): 高解像度の入力を与えることで画像中の詳細なパターンを獲得できる
スケーラの扱い
$$ \begin{aligned} & \text { depth: } d=\alpha^\phi \ & \text { width: } w=\beta^\phi \ & \text { resolution: } r=\gamma^\phi \ & \text { s.t. } \alpha \cdot \beta^2 \cdot \gamma^2 \approx 2 \ & \alpha \geq 1, \beta \geq 1, \gamma \geq 1 \end{aligned}$$
- 単一の係数Φによりネットワークのスケーリング 畳み込みの演算量FLOPSは$d,w^2,r^2$に比例 (CNNにおいては畳み込み演算が計算コストを占領するため、d,w,rを制御するのが良い)
- 制約条件の式より、ネットワークのFLOPSは約$2^\phi$でスケーリング
- アルファ、ベータ、ガンマはグリッドサーチにより適切な値を定数として扱う
最適化問題
目的関数をAccuracyとして、 使用するメモリ容量と、処理能力(FLOPS)の制約を満たす条件下で最大化を目指す
$$ \begin{array}{ll}\ \max {d, w, r}&\operatorname{Accuracy}(\mathcal{N}(d, w, r))\ \text { s.t. }&\mathcal{N}(d, w, r)=\bigodot{i=1 \ldots s} \hat{\mathcal{F}}_i^{d \cdot \hat{L}i}\left(X{\left\langle r \cdot \hat{H}_i, r \cdot \hat{W}_i, w \cdot \hat{C}_i\right\rangle}\right)\ &\operatorname{Memory}(\mathcal{N})\leq\text { target_memory } \ &\operatorname{FLOPS}(\mathcal{N})\leq\text { target_flops } \ \end{array} $$
- 制約条件の第一式はネットワークの定義式
- Residualブロックなどの処理ブロック一つをステージとしてiを用いて表現
- ハットマークはスケーラの1単位あたりの量をしめす
- Lについては1ステージあたりの畳み込み演算回数
参考文献レポート(スケーリングと精度の対応)
原著論文において、個別のスケーラーごとに計算量を上げたときの正解率と提案された複合スケーラでの計算量を上げたときの正解率があったので、掲載する。
計算量を上げたときのパフォーマンス向上は複合スケーラが勝っていることは明らかで、 単一のスケーラの向上は頭打ちが見られたものの、複合スケーラの方ではまだ精度が上がる余地があるように思われる。
<イメージネットとスケーラの対応>
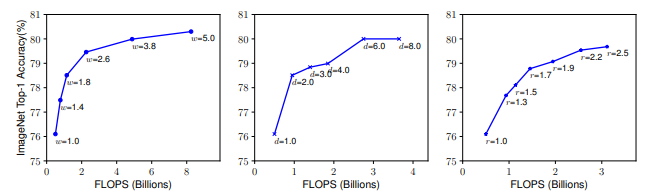
<EfficientNetとスケーラ、複合スケーラの対応>
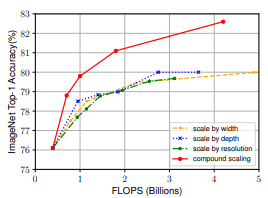 (M. Tan and Q. V. Le, “EfficientNet: Rethinking model scaling for convolutional neural networks,” in Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 2019, pp. 6105-6114.)
(M. Tan and Q. V. Le, “EfficientNet: Rethinking model scaling for convolutional neural networks,” in Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 2019, pp. 6105-6114.)
物体検知とSS解説
物体認識周りのタスクの概観
 ※SemanticとInstanceの違いは同属性・別個体を分けるかどうか
(講義スライドより引用)
※SemanticとInstanceの違いは同属性・別個体を分けるかどうか
(講義スライドより引用)
データセット
物体検出コンペで使われたデータセットの比較
| データセット名$^{※1}$ | クラス数$^{※2}$ | Train+Val | Box/画像$^{※3}$ | 画像サイズ | BB形式 | Segmentation data |
|---|---|---|---|---|---|---|
| VOC12 | 20 | 11540 | 2.4 | 470 × 380 | (x_min, y_min, x_max, y_max) | 無 |
| ILSVRC17 | 200 | 476668 | 1.1 | 500 × 400 | (x_min, y_min, x_max, y_max) | 無 |
| MS COCO18 | 80 | 123287 | 7.3 | 640 × 480 | (x_min、y_min、width、height) | 有 |
| OICID18 | 500 | 1743042 | 7 | 一様ではない | (x_min, y_min, x_max, y_max) | 無 |
| (講義スライドより引用) |
※1:CIFAR-10/CIFAR-100, Food-101, 楽天データ(文字領域アノテーション画像)など他にもデータセットは存在する ※2:クラス数が大きいことは細かすぎる違いがあるケースもあって、必ずしも良いこととは言えない →ラベル変換すれば良いので、どうとでもできる ※3:Box/画像の値は、大きいほど日常生活に近い重なりを含んだ画像になり、小さいほどアイコニックで検出し易い画像になる
<代表的データセットのポジショニングマップ>
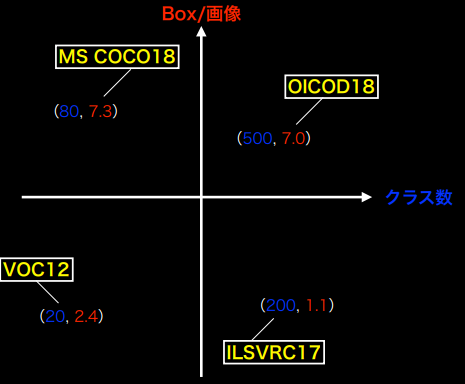 (講義スライドより引用)
(講義スライドより引用)
評価指標
IoUを固定してmAPを算出する IoUを変化させたときの平均を取った$mAP_{COCO}$という指標もある
クラス分類
表
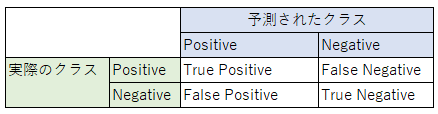 ※True/Falseは正誤、Positive/Negativeは陽性/陰性を示す
※True/Falseは正誤、Positive/Negativeは陽性/陰性を示す
指標
- Accuracy: $\frac{TP+TN}{TP+FP+TN+FN}$ 正解率とよばれ、全データのうち、正しく分類できたサンプルの割合を示す
- Precision :$\frac{TP}{TP+FP}$ 精度と呼ばれ、陽性と判定したもののうち、実際に陽性だった割合を示す
- Recall :$\frac{TP}{TP+FN}$ 検出率とよばれ、陽性のデータのうち、陽性と正しく判定できた割合をしめす
- (Specificity):$\frac{TN}{TN+FP}$ 特異度とよばれ、陰性のデータのうち、陰性と正しく判定できた割合をしめす ※検出率の陰性データ版
概要
- 縦軸にPrecision(精度)、横軸にRecall(再現率)を取ったグラフで、閾値を変化させたときの2変数の推移を描画する
- モデルごとに一つの曲線が描かれる
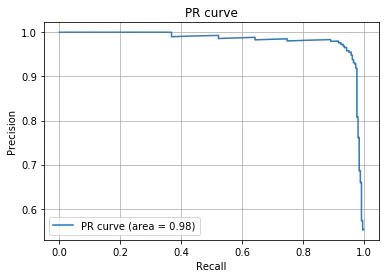
使い方
- 分類の閾値を変化させたときのトレードオフの関係を見て閾値を設定するために用いる
- モデル自体の良さはAP(Average Precision)を用いて判定
※似た考え方にROC曲線があるが、PRカーブはデータの不均衡の影響を特に受けるので、不均衡データに対して使用すると良い
mAP
PR曲線の下側の面積、閾値Rを0~1の範囲でPrecisionを積分したときの値 $$AP = \int_0^1 \operatorname{P}(R) dR$$ $$mAP = \frac{1}{C}\overset{N}{\underset{i=1}\sum{AP_i}}$$ 他クラス分類のときはmAP(mean Average Precision)が使われる ※Cはクラス数 モデルの利用目的ごとに適切な閾値の設定を行う
Bounding Boxの予測性能
指標:IoU (Intercection over Union) ※別名Jaccard係数
※Ground Truthの中のTPでもなく、予測したBounding BoxのなかのGTでもないことに注意
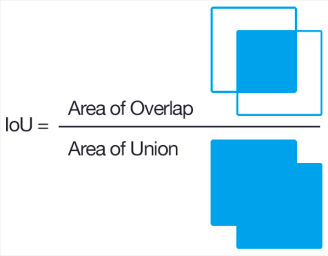 (講義スライドより引用)
(講義スライドより引用)
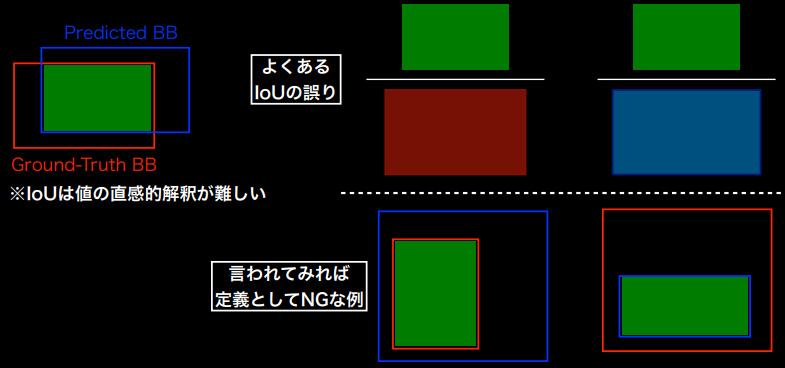 (講義スライドより引用)
(講義スライドより引用)
実利用上の指標
検出速度:FPS
物体検知の流れ
AlexNet以前はSIFT(Scale Invariant Feature Transform:スケール不変特徴量変換)が主流だったが 現在はDCNNが主流
ネットワークの発展 2012~2018
- AlexNet(DCNN)
- Inceptionモジュール
- Residualブロック
- Denseブロック
- MobileNetなどの軽量化
物体検知フレームワークの発展 2013~2018
- DetectorNet
- RCNN
- Fast,FasterRCNN
- YOLO
- SSD
検出ステップ数での分類
- 2段階検出器:候補領域の検出とクラス推定を別々に行う
- 精度は高い傾向
- 計算量が大きく推論も遅い傾向
- 1段階検出器:候補領域の検出とクラス推定を同時に行う
- 精度が低い傾向
- 計算量が小さく推論も速い傾向
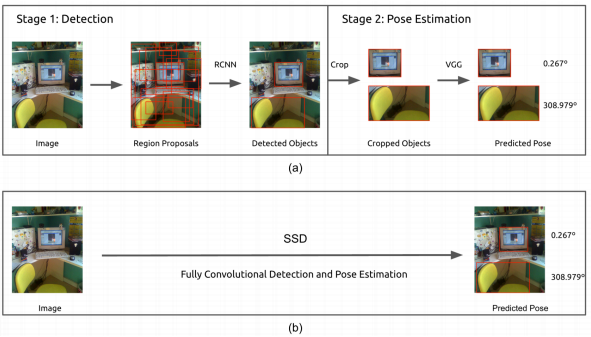 (P. Poirson, P. Ammirato, C.-Y. Fu, W. Liu, J. Kosecka, and A. C. Berg, “Fast single shot detection and pose estimation,” arXiv preprint arXiv:1609.05590, 2016.)
(P. Poirson, P. Ammirato, C.-Y. Fu, W. Liu, J. Kosecka, and A. C. Berg, “Fast single shot detection and pose estimation,” arXiv preprint arXiv:1609.05590, 2016.)
Single Shot Detector
SSDの概観
- Default Boxを用意
- 検出物体に合わせてDefault Boxを変形して、Confidenceを出力
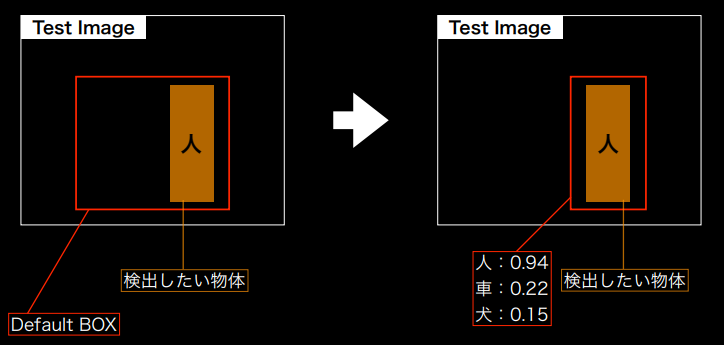 (講義スライドより引用)
(講義スライドより引用)
ネットワークアーキテクチャ
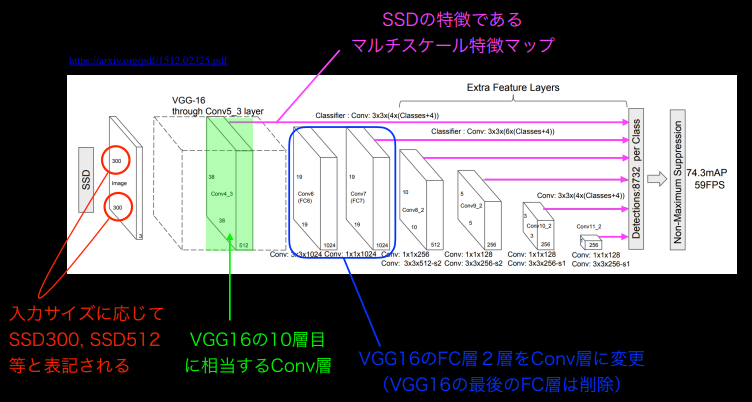 (講義スライドより引用)
(講義スライドより引用)
特徴マップからの出力
各クラスのConfidence+デフォルトボックスの調整項がマップ別に設定される特徴量あたりのDefault Box個数分あって、それを特徴マップサイズ分持つ
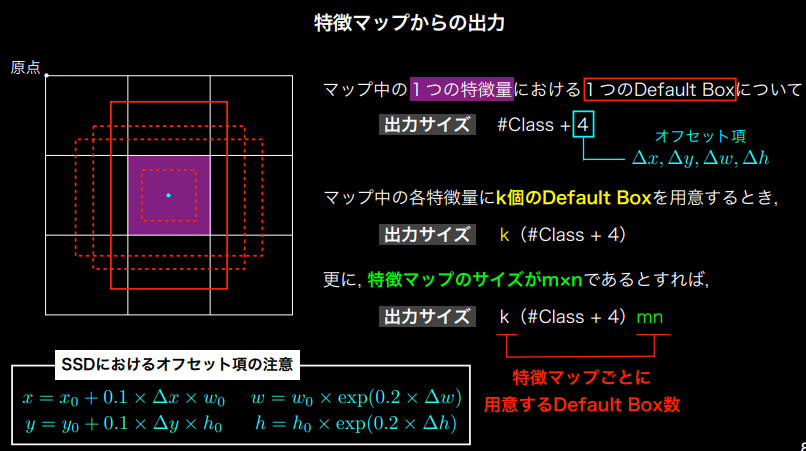 (講義スライドより引用)
(講義スライドより引用)
※SSDでは層ごとに特徴量あたりのDefault Box数を変更しているが、これは計算量との兼ね合いで変更しているだけで特に深い意味があるわけではない
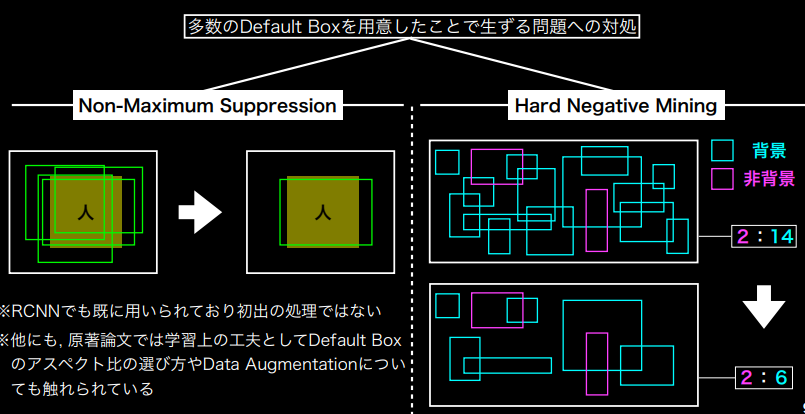
DefaultBoxが多いときに発生する問題とその対応
- Non-Maximum Suppression: 一つの物体しかなくても、複数のDefault Boxが生成されて冗長になってしまう →IoUで一定以上のモノはConfidenceが高いものを残して削除する
- Hard Negative Mining:背景と非背景の不均衡が発生する
→割合に制限をかけて背景の生成を抑える
 (講義スライドより引用)
(講義スライドより引用)
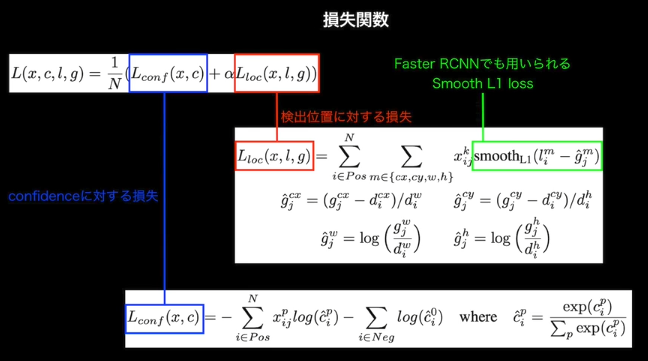
損失関数
クラス分類に関する損失と、物体検出した位置に関する損失をあわせて評価する
 (講義スライドより引用)
(講義スライドより引用)
Semantic Segmentation
ピクセルごとにクラス情報を持つためには、畳み込みでダウンサンプリングしてきたものを入力と同サイズまでアップサンプリングする必要がある
ダウンサンプリングしないという選択肢は受容野と計算量、メモリの兼ね合いから難しいため、 うまくアップサンプリングしていく必要がある
-
転置畳み込み(逆畳み込み)
- 入力特徴マップのpixel間隔をStride分あける
- 特徴マップの外周に(kernelsize-1) - padding分だけ余白を足す
- 畳み込み演算を行う
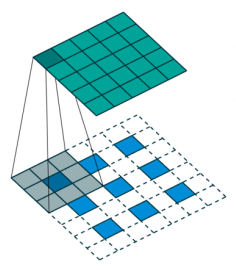 (講義スライドより引用:k=3,p=1,s=1で青が入力、灰色がカーネル、緑が出力)
(講義スライドより引用:k=3,p=1,s=1で青が入力、灰色がカーネル、緑が出力)
-
輪郭情報の補完
- Pooling層の出力をelement-wise addition (FCN)
- スキップ接続 Encoderの特徴量マップを対応するデコーダーの入力に連結する (U-Net)
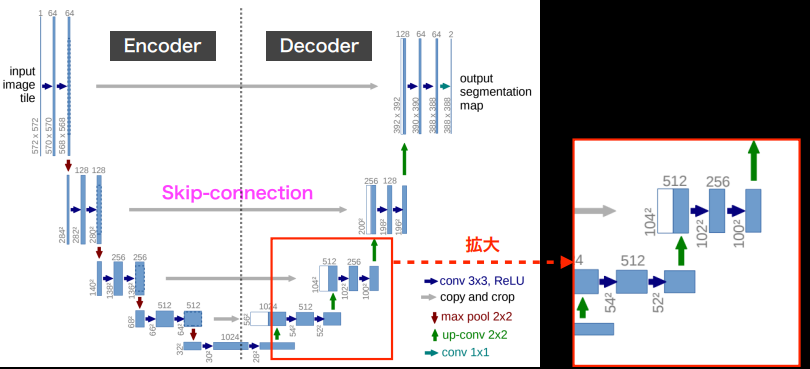 (講義スライドより引用)
(講義スライドより引用) - Unpooling:Pooling時に採用した位置のインデックス情報を保持しておいてアップサンプリング時に活用
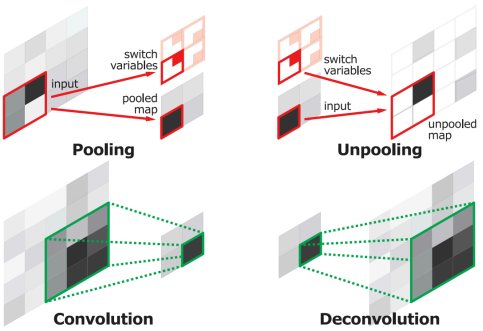 (講義スライドより引用)
DeconvNet(上)とSegNet(下)
※SegNetではUpSamplingにおいて、逆畳み込みは行っておらず、Unpoolingのみ、これによってメモリ効率がよく高速に動作する
(講義スライドより引用)
DeconvNet(上)とSegNet(下)
※SegNetではUpSamplingにおいて、逆畳み込みは行っておらず、Unpoolingのみ、これによってメモリ効率がよく高速に動作する
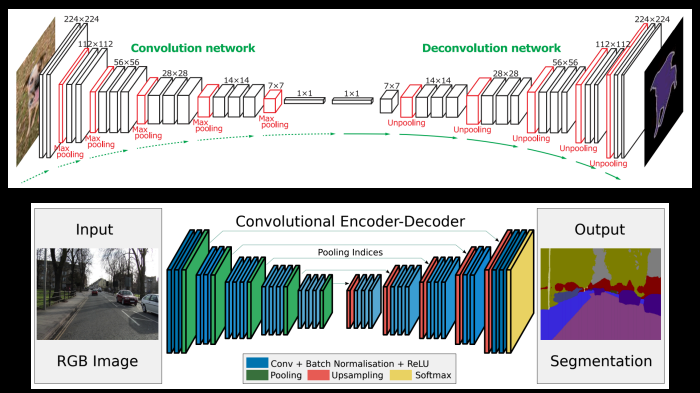 (講義スライドより引用)
(講義スライドより引用)
CNNと受容野
猫はどちらか?
 (講義スライドより引用)
(講義スライドより引用)
受容野を広げる方法
- Pooling (ストライド)
- 畳み込み
- 層を深くする ※計算量、メモリの問題がでる
- Dilated Convolution (畳み込みの際に入力を隙間を空けて要素を取るようにする)
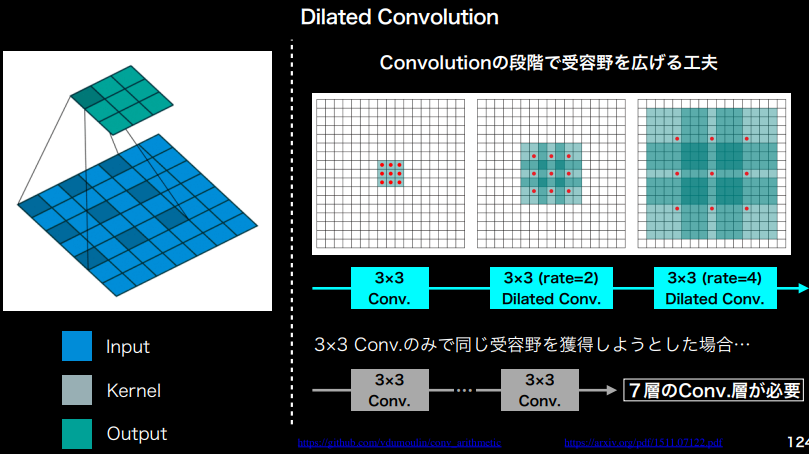 (講義スライドより引用)
(講義スライドより引用)
参考記事レポート
認定テスト内で、SSDについて正誤を問う内容がでた。
SSDが小さな物体検出が苦手かどうか、VOC07とVOC12のクラス数について迷ったが、
原著論文"https://arxiv.org/pdf/1512.02325.pdf” において、オブジェクトのサイズと精度の比較が出ていた。
(新しいデータ拡張で改善できたという文脈)
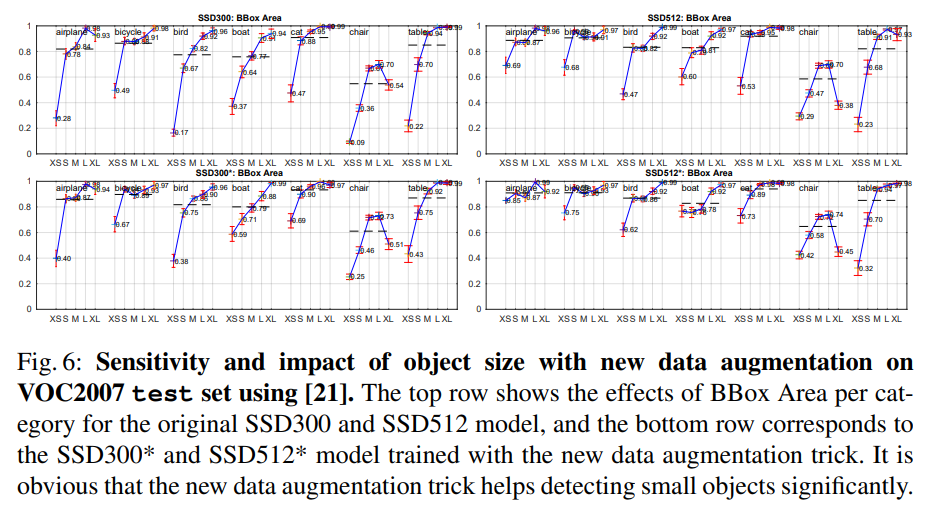 (Wei Liu,SSD: Single Shot MultiBox Detector,“https://arxiv.org/pdf/1512.02325.pdf”“Arxivより引用)
(Wei Liu,SSD: Single Shot MultiBox Detector,“https://arxiv.org/pdf/1512.02325.pdf”“Arxivより引用)
認定テストでデータセットに関する問題が出たため、以下の参考サイトで確認 OICID 2018:“https://github.com/openimages/dataset/blob/main/READMEV3.md" “https://storage.googleapis.com/openimages/web/factsfigures_v7.html" ILSVRC17:“https://www.kaggle.com/competitions/imagenet-object-localization-challenge/data" Pascal VOC形式でバウンディングボックスを表現しているとされているが、kaggle特有なのか、もとからそうなのか不明 MS COCO: https://cocodataset.org/#format-results
フリマアプリの利用に向くかどうかは、アイコニックな画像なのかどうかの基準で、講義で触れられたBB/画像の値で判定し、Segmentationデータの有無は参考サイトをもとにして要約中の表に記載した。
Mask R-CNN
R-CNN (Reginal CNN)
- 関心領域 Region of Interestを切り出す
- 切り出した関心領域の画像のサイズを調整
- CNNによって特徴量を求める
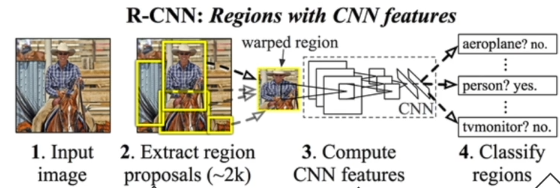 (講義スライドより引用)
(講義スライドより引用)
問題点:関心領域の切り出しで1秒、CNNで0.22秒という処理時間、リアルタイム処理には遠い
Fast R-CNN
RCNN:関心領域ごとにCNNに入力 Fast R-CNN :画像全体をCNNに入力して、特徴量を抽出したFeature Mapに対してROIに対応する部分を抽出、サイズ調整するROI Poolingを行う
→ 計算量を大幅に削減
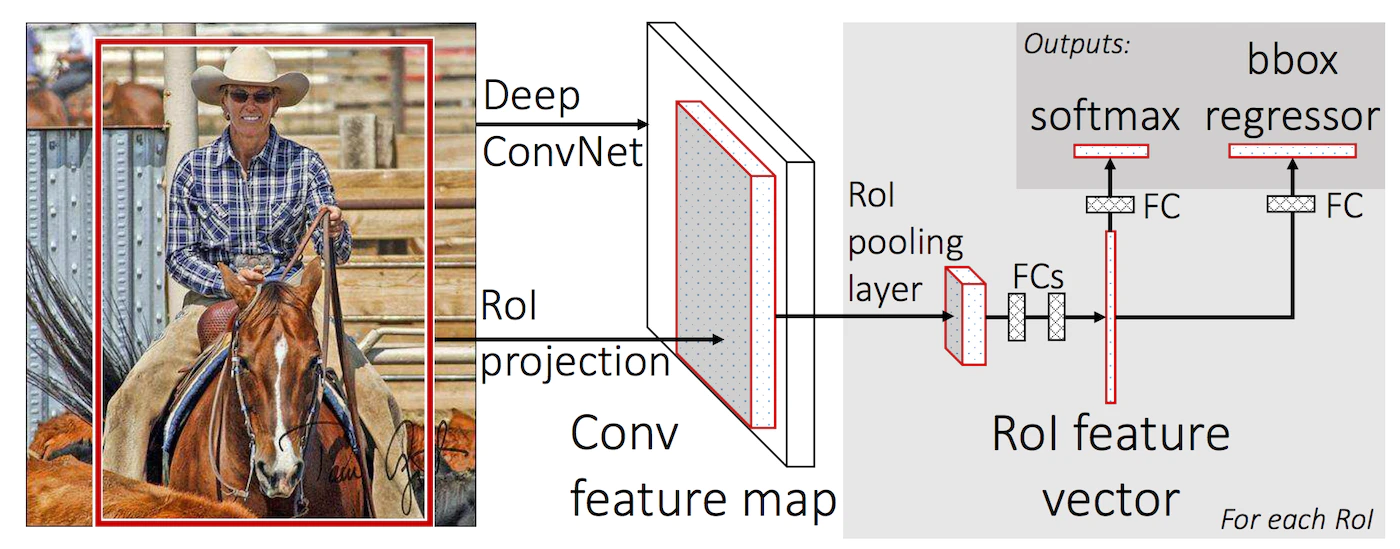 (R. Girshick, “Fast R-CNN,” in Proc. of ICCV, 2015より引用)
※ROI poolingでは入力画像と特徴量マップの解像度が異なるために、実際の画像のROIとROI Poolingで対応する領域が異なる問題がある
(参考:“https://qiita.com/yu4u/items/5cbe9db166a5d72f9eb8")
(R. Girshick, “Fast R-CNN,” in Proc. of ICCV, 2015より引用)
※ROI poolingでは入力画像と特徴量マップの解像度が異なるために、実際の画像のROIとROI Poolingで対応する領域が異なる問題がある
(参考:“https://qiita.com/yu4u/items/5cbe9db166a5d72f9eb8")
ROI Pooling
- Region Proposal の座標を整数に丸めて対応する領域定める
- 領域を固定サイズになるように等分する
- 等分された各領域に含まれるピクセルの値の平均か最大を用いて各領域の値を決定する ※このとき各ピクセルは等分された領域のいずれか一つに割り当てられる
1の丸めと、3のピクセルの割り当て方によって位置ずれが発生する
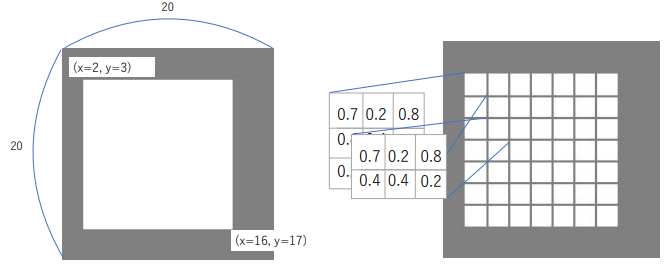 (講義スライドより引用)
(講義スライドより引用)
Faster R-CNN
関心領域の切り出しもCNNで行う (Region Proposal Network) →リアルタイムで動作、動画認識への応用が可能に and End-to-Endでの学習
※R-CNN系の処理の処理時間はCNN以外の部分が大半を占めていたため、CNNで完結することでかなりの高速化がなされた
Region Proposal Network
- 特徴マップ上のすべての点にAnchor Pointを設定し、そのPointごとにAnchor BoxをS個作成
※特徴マップがH×WならAnchor PointはH×W
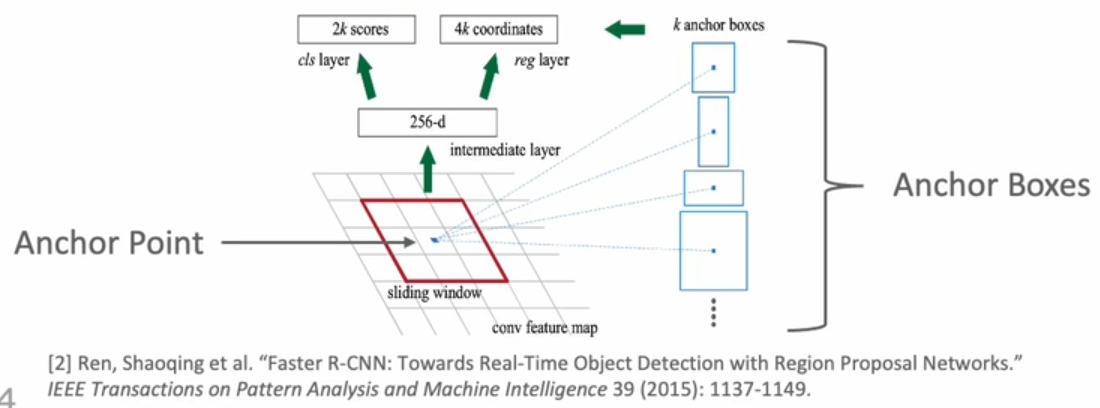
- Ground TruthとBoxを比較して、背景と物体の2値と座標のズレ(中心、幅、高さ)の4変数を出力する
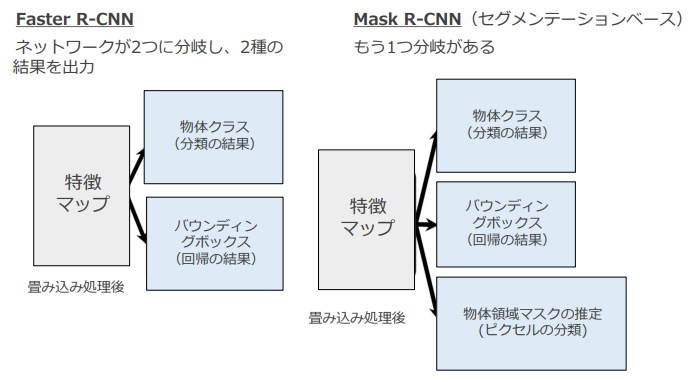
Mask R-CNN
“https://arxiv.org/abs/1703.06870"
- Faster R-CNNの拡張
- 物体検出結果で得られた領域に限定してセグメンテーションを行うことで効率アップ
 (講義スライドより引用)
(講義スライドより引用)
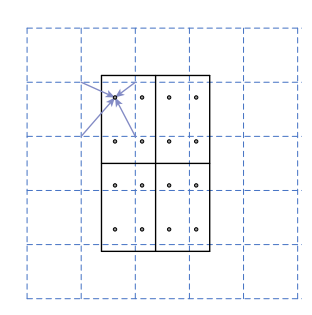
ROI Align
[ROI Pooling](#ROI Pooling)の位置ずれ問題に対応
- (丸め込みは行わない)
- N×Nの固定領域の際は候補領域を縦横でN等分ずつにする
- 区切られた各領域内に4つ点を設定する
- 各点の値をBilinier Interpolationで最近傍の4ピクセルの値を使って算出する
- 4点の値を平均または最大で代表値にまとめる
 (Mask R-CNN, “K. He, G. Gkioxari, P. Dollar, and R. Girshick, in Proc. of ICCV, 2017.より引用)
(Mask R-CNN, “K. He, G. Gkioxari, P. Dollar, and R. Girshick, in Proc. of ICCV, 2017.より引用)
参考文献レポート
ROI Alignについて、点の決定方法が曖昧だったため、原著論文等を確認した、 原著論文によると、点の数や位置の影響は小さいとのことで、適当に決めて良いようである。 4点取らずとも単純に区切った領域の中心でInterpolationしても精度が出るとのこと、 “https://arxiv.org/pdf/1703.06870.pdf"
黒本において、P241にR-CNNの問題があった。 Selective Searchの方法、検知速度が遅い問題から、Fast,Faster R-CNNの内容が問われた。
FCOS Fully Convolutional One-Stage Detection
問題意識:Bounding Boxを出力する前に大量のAnchor Boxを作成している
- ハイパーパラメータとなっていて設定次第で精度が大きく変わってしまう
- 角度やサイズなどの影響が強くでてしまう
- 前景と背景の不均衡
手法
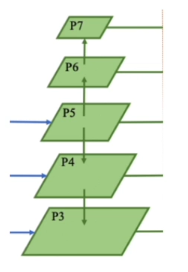
FPN(Feature Pyramid Networks):複数サイズの特徴マップを利用 →全体特徴を捉えると同時に細かいローカルな特徴も捉える →画像上の位置的に重なっているクラスも別のレベルのマップで捉えられる
 (講義スライドより引用)
(講義スライドより引用)
出力
- ピクセルごとのクラスラベル
- 各ピクセルから物体領域のボックスの4辺までの距離
ポジティブサンプルとネガティブサンプルの分け方 →ラベルの領域にピクセルが含まれる∧クラスが一致
centerness:縦横の4辺までの距離を大きい方で小さい方を割った値の幾何平均
損失関数
クラス間のサンプルの不均衡を考慮したFocal Lossと位置ずれに関する損失関数IoU Lossを計算している (GT:Ground Truth,PA:Predicted Area)
$$Focal_Loss(p_t) = -(1-p_t)^\gamma log(p_t)$$ $$IoU_Loss = 1 - \frac{GT\cap PA}{GT\cup PA}$$
参考文献レポート
Focal Lossについて提案論文で確認した
論文中では$\gamma=2$となっている,$\gamma=0$はクロスエントロピーロスになる
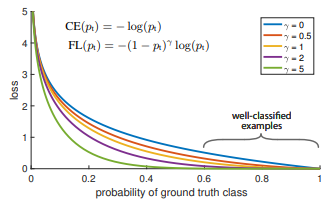 (T.-Y. Lin, P. Goyal, R. Girshick, K. He and P. Dollar, “Focal Loss for Dense Object Detection,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 42, no. 2, pp. 318-327, 2020.“https://arxiv.org/pdf/1708.02002.pdf")
(T.-Y. Lin, P. Goyal, R. Girshick, K. He and P. Dollar, “Focal Loss for Dense Object Detection,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 42, no. 2, pp. 318-327, 2020.“https://arxiv.org/pdf/1708.02002.pdf")
またセグメンテーションに使われる損失関数にどういったものがあるのか確認した。
セグメンテーション周りの損失関数まとめ
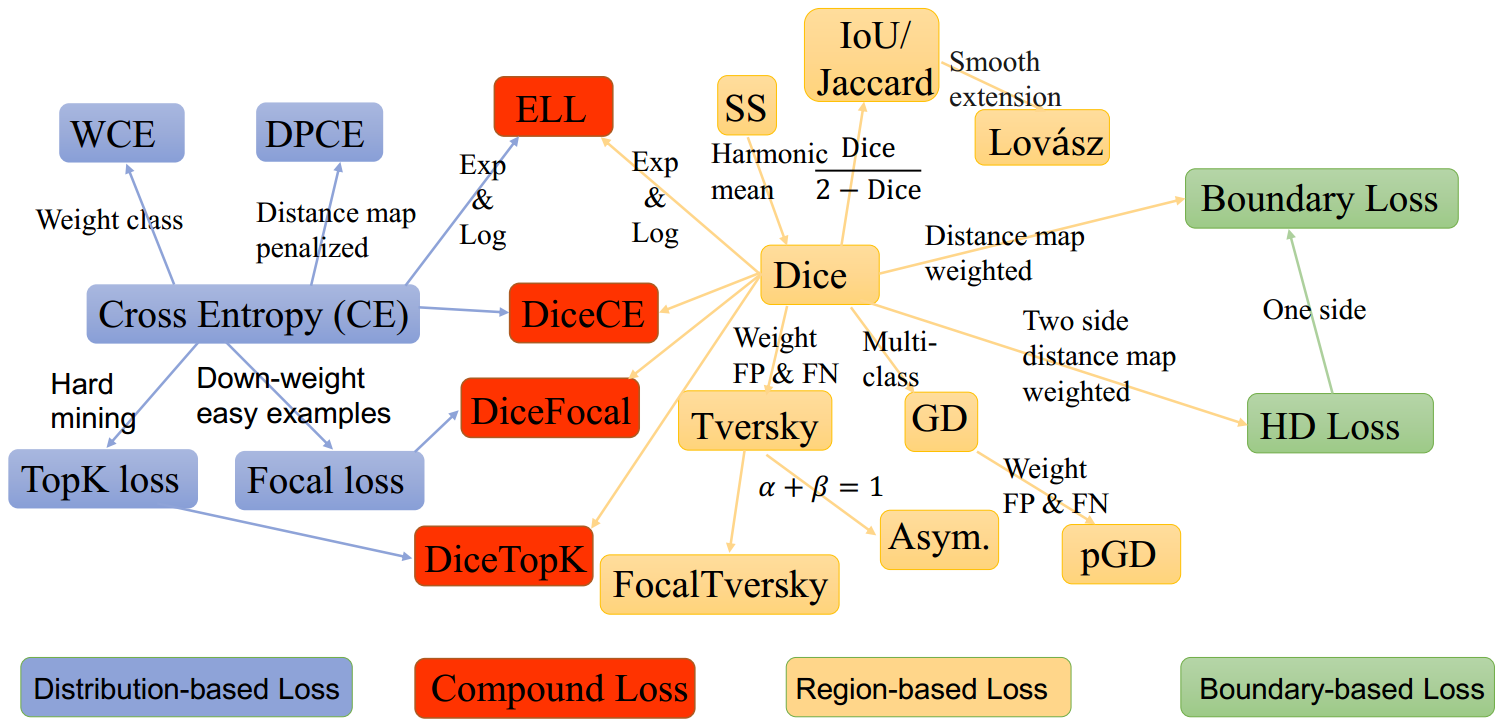
“https://github.com/JunMa11/SegLoss”
Transformer
RNNと言語モデル
言語モデル:単語の並びに確率を与える(単語の並びが文章として自然なのかを確率で評価する) 同時確率を事後確率の総乗で表現する
$$P(w_1,w_2,\dots,w_m) = \overset{m}{\underset{i=1}{\prod}}P(w_i|w_1,w_2,\dots,w_{i-1})$$
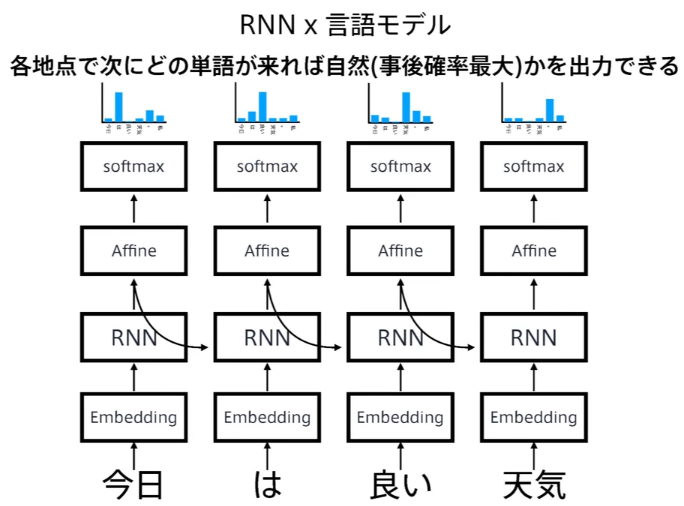 (講義スライドより引用)
(講義スライドより引用)
Seq2Seq
Encoder RNNで文脈ベクトル(最終内部状態)を生成して、それをDecoder RNNの初期内部状態にして単語生成していく
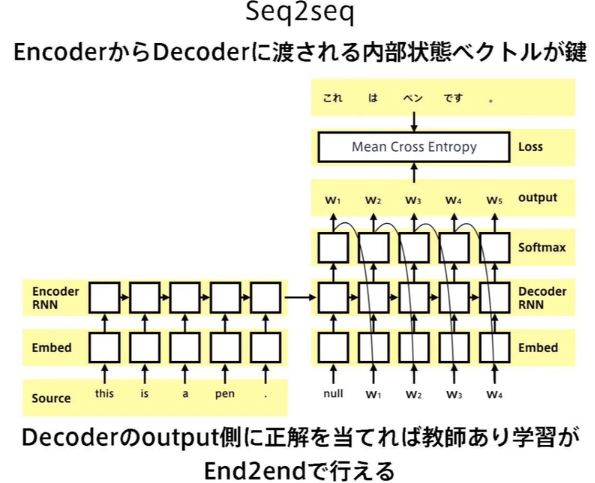 (講義スライドより引用)
(講義スライドより引用)
Beam Search
各時刻において選ぶ単語をk個にして、各時刻において確率が高いものから順にk個の出力系列を保持してデコーダー出力を出していく
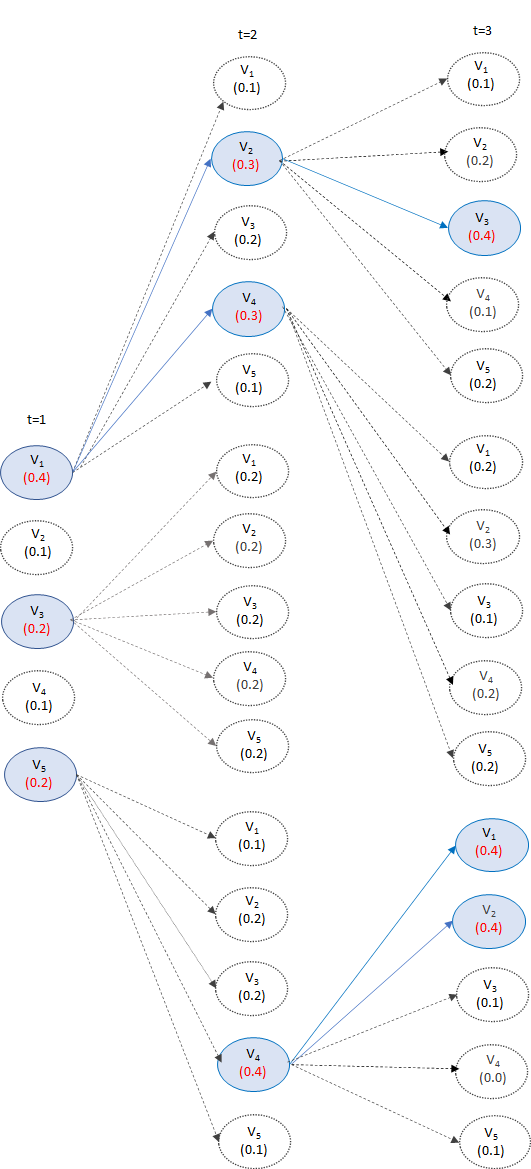 (“https://data-analytics.fun/2020/12/16/understanding-beamsearch/#toc3" より引用,k=3、ボキャブラリーが5の例)
(“https://data-analytics.fun/2020/12/16/understanding-beamsearch/#toc3" より引用,k=3、ボキャブラリーが5の例)
Encoder-Decoderモデルの弱点
翻訳本の文章を一つのベクトルで表現する →入力系列が長くなるとベクトルの表現力が足りなくなる (系列が長くなったときに統計的機械翻訳モデルに比べて顕著に精度低下が見られる)
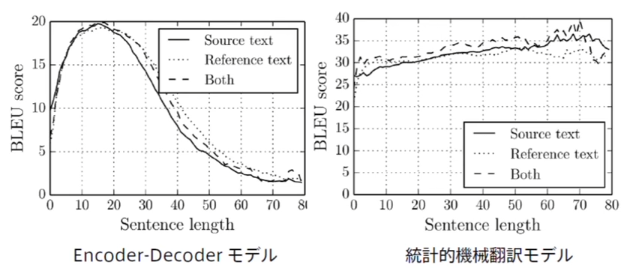 (講義スライドより引用)
(講義スライドより引用)
どうするのか?
→ Attention機構
Attention機構
簡単にいうと辞書オブジェクト
入力の検索クエリに一致するKeyをボキャブラリから索引して、対応するValueを取り出す操作
固定次元の単語ベクトルにEmbedingされた各トークンを線形写像によってValue,Query,Keyに変換する
- Value: そのトークンから得られる「値」
- Query: 関連の強い別のトークン(自分自身も含む)を知り、そのValueを得るための「問い合わせ」
- Key: 自分自身や別のトークンのQueryから問い合わせを受ける「索引」 問い合わせてきたQueryからの関連性を計算し、それに応じて自身に結びついたValueを返すために存在
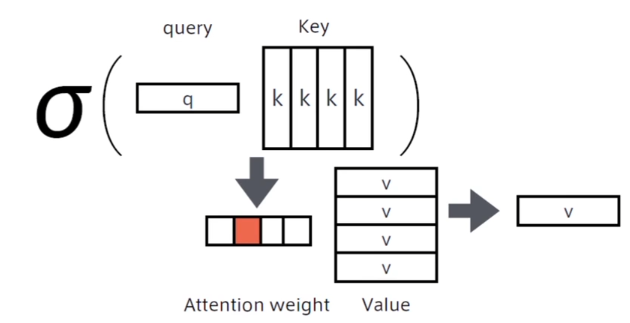 (講義スライドより引用)
(講義スライドより引用)
Attentionの導入によって、精度が低下しなくなった。
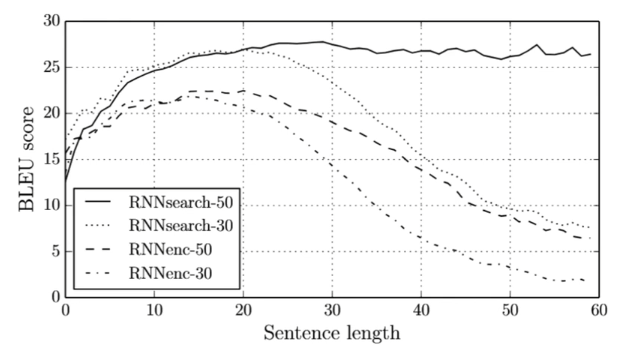 (講義スライドより引用)
(講義スライドより引用)
Transformer
- 2017 June
- RNNを使わない Attentionだけ
- 3600万文を8GPUで3.5日など圧倒的に低いコストでSOTAを実現
ネットワークアーキテクチャ
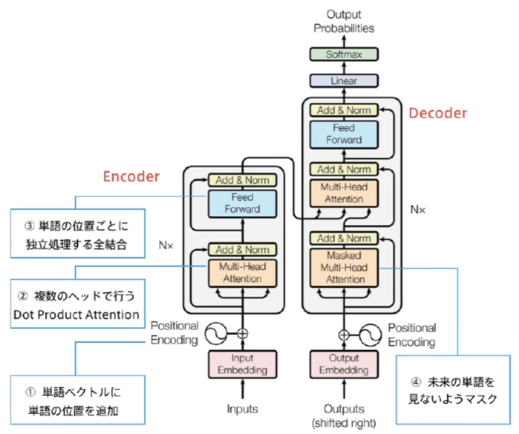 (講義スライドより引用)
(講義スライドより引用)
2種類のAttention
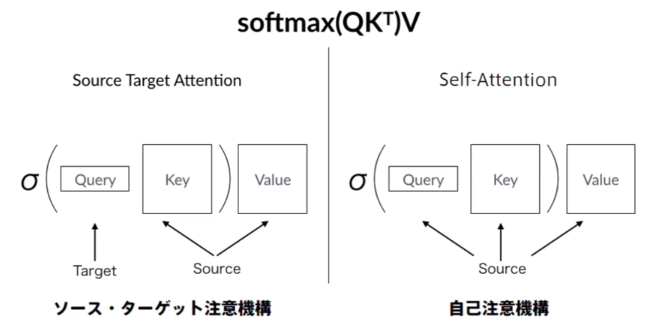
2種類のAttention があるが、Transformerで使われるのはSelf-Attention
 (講義スライドより引用)
(講義スライドより引用)
Self Attentionは、どの時刻のエンコードを行う場合も入力は入力系列全体で同じ
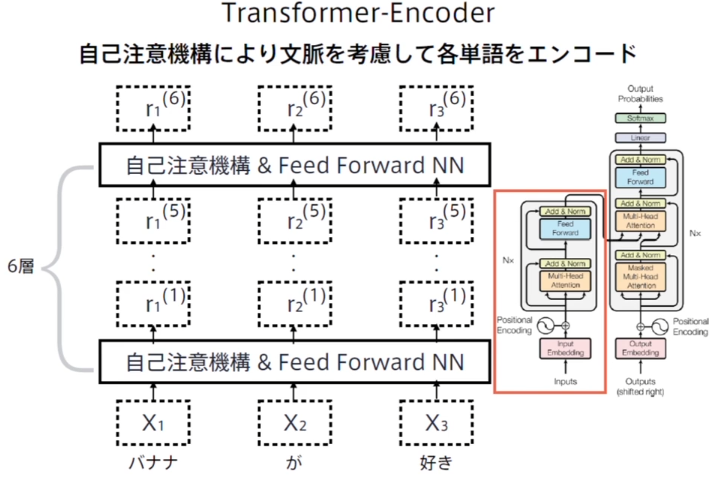
Point-Wise Feed-Forward Networks
位置情報を保持したまま順伝播させる(出力の形状が入力と同じになる)ために、入力に対して掛ける重みの行列のサイズを定める
※512は系列長、2048は隠れ層のノード数

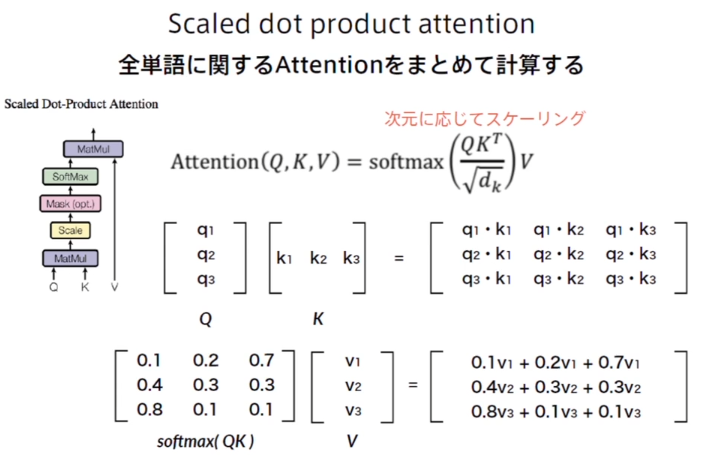
Scaled dot product attention
- 入力系列をQuery,Key,Value行列に線形変換
- AttentionのためのqueryとKeyの行列積 (内積によって関連の強さを返す)
- Softmaxで勾配消失することを防ぐためのスケーリング (ベクトル次元数の平方根で割る)
- Unknownなどの特別なトークンを処理するためのマスク機構
- ソフトマックスで全確率が1になるようにする
- valueを対応する確率で荷重平均する (行列積)
※下図のq1,k1,v1などはベクトルでスカラーではないことに注意
 (講義スライドより引用)
(講義スライドより引用)
Multi-Head Attention
畳み込みのチャネル違いのようなモノ、異なる特徴を捉える
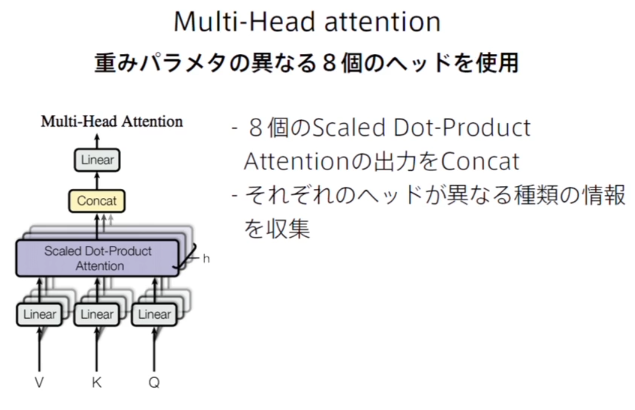
Positional Encoding
RNNと違い、Attention機構のみだと、単語の位置情報を保持できない →Positional Encodingを行う
Positional Encodingとは、
単語の埋め込みベクトル + 位置情報ベクトル を Attentionへの入力とする
このとき、位置情報ベクトルは
- 文章の長さに関係なく、それぞれの位置が同じ位置ベクトルに対応する必要がある
- 埋め込みベクトルに対して位置情報ベクトルが大きくなりすぎては行けない → $${PE\left( pos,2i\right) =\sin \left( \dfrac{pos}{10000^{2i/d_{model}}}\right) }$$
$${PE\left( pos,2i+1\right) =\cos \left( \dfrac{pos}{10000^{2i/d_{model}}}\right) }$$
※10000はハイパーパラメータでどれだけ長い文章が来ても同じ値にならないために十分大きな値を取っている ※位置情報ベクトルの系列後半だと(iが大きくなると)周波数が小さな値となり、位置の変化の影響が小さくなる。
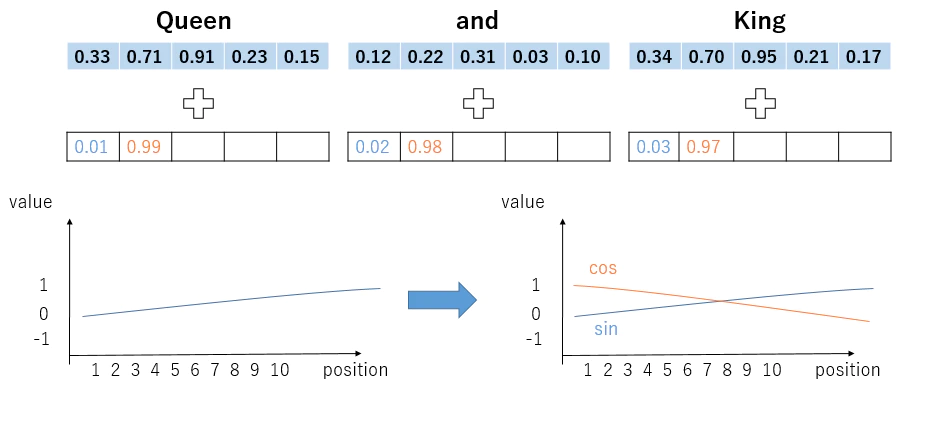 参考:”Positional Encodingを理解したい - Qiita:https://qiita.com/snsk871/items/93aba7ad74cace4abc62”
参考:”Positional Encodingを理解したい - Qiita:https://qiita.com/snsk871/items/93aba7ad74cace4abc62”
こちらは絶対位置を利用しているとのことだが、相対位置を利用する方法だと、 データセットで学習したより長い系列情報を入れてデータ生成させても破綻しないとのこと。
考察
位置符号化でややこしい三角関数を使っているのは ”(普通の)三角関数による出力を位置符号の値として用いようとしてしまうと,周期ごとに同じ値が出力されてしまい,お互い独立した位置符号値を,各pos番目のトークンに与えることができない.” (参考:“https://cvml-expertguide.net/terms/dl/seq2seq-translation/transformer/positional-encoding/") からとされているが、 ハイパーパラメータの10000を十分大きくすれば、通常の三角関数でも大丈夫な様に思われる。こちらの方がわかりやすく時系列データに対する1次元畳み込みによる周波数成分抽出で位置情報をNN演算で復元できるように感じるが、 単語ベクトルと合成したときのS/N比や、長い系列に対して周波数を大きくすることで位置が少しズレたときの差分が分からなくなる問題が考えられるが、実際のところはもう少し調べないと分からない。
その他の学習上の工夫
- Residual Connection (Add)
- 実装上は入力を出力に加算して次のブロックに渡すだけ →勾配の安定化によって学習・テスト誤差の低減
- Layer Normalization
- 各層においてバイアスを除く活性化関数への入力を平均0,分散1に正規化 →学習の高速化と安定化
Attentionの可視化
言語構造が捉えられている様に思われる
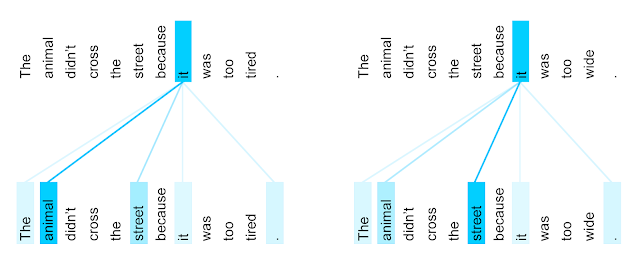 (講義スライドより引用)
(講義スライドより引用)
確認問題
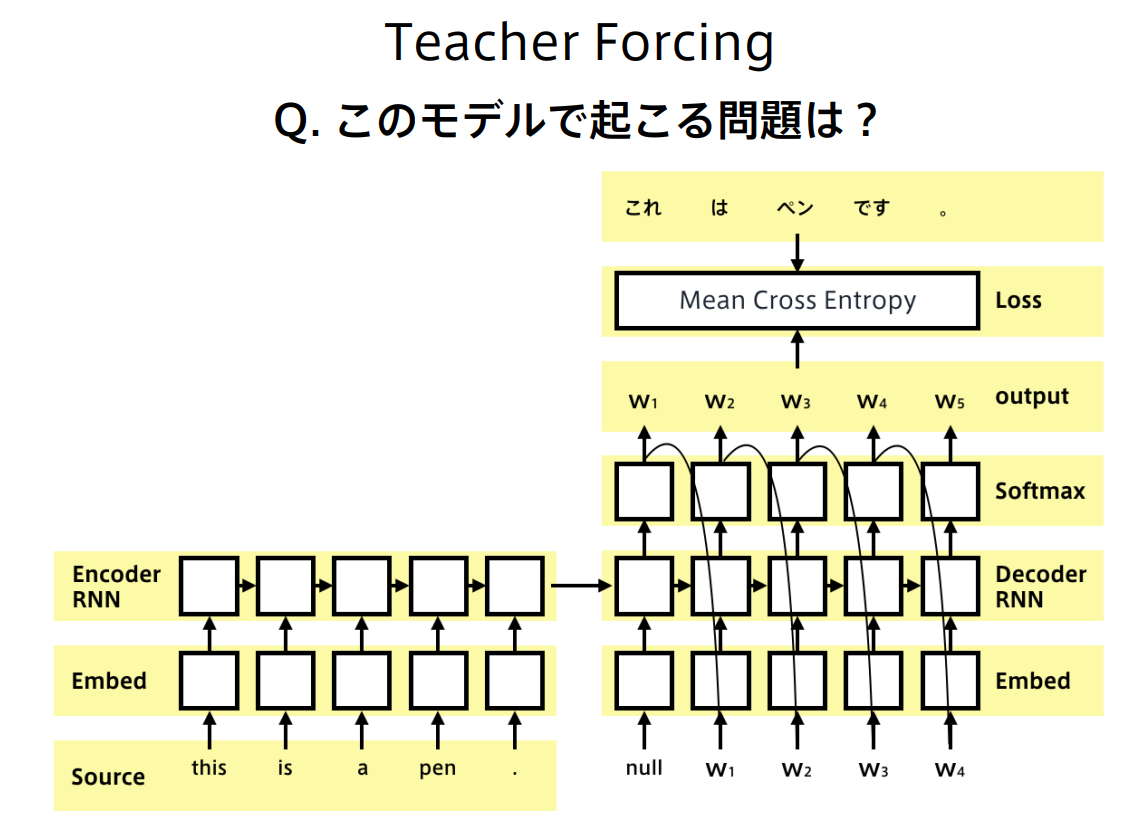 時刻tのデコーダ出力をt+1のデコーダー入力に使っているため、誤差が蓄積していく、連鎖的に大きくなっていく問題があり、学習が安定せず、収束がおそい
時刻tのデコーダ出力をt+1のデコーダー入力に使っているため、誤差が蓄積していく、連鎖的に大きくなっていく問題があり、学習が安定せず、収束がおそい
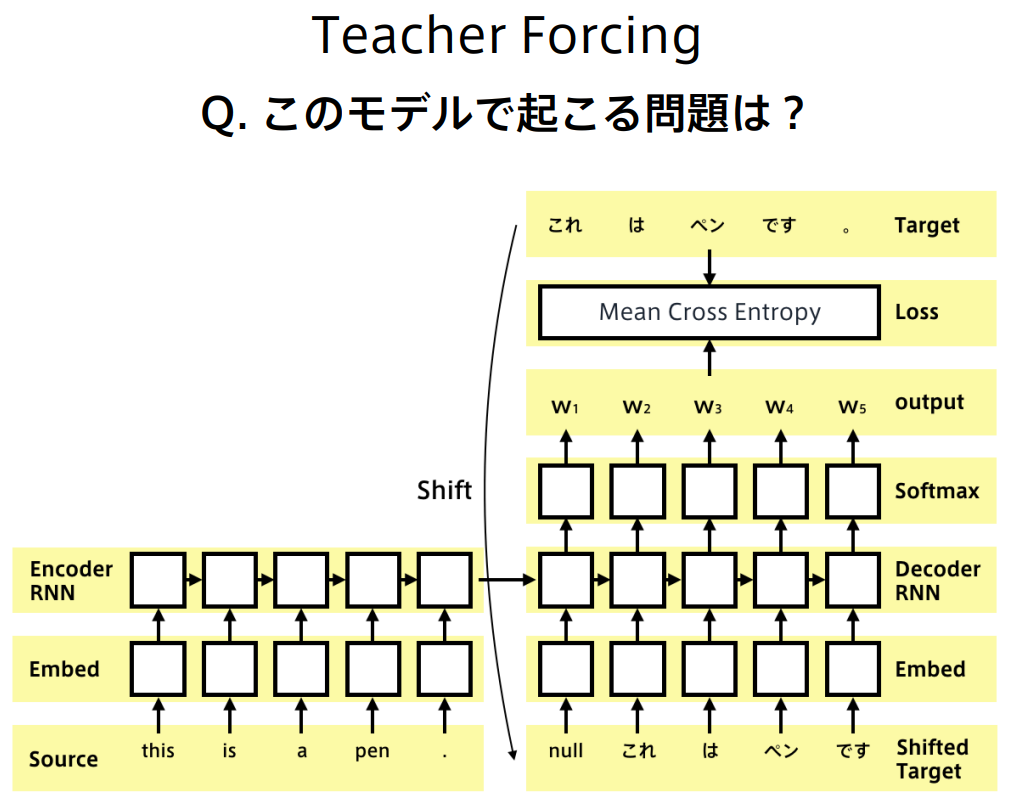 誤差が連鎖的に大きくなる問題に対応するために、
一つ前の時刻のターゲットをデコーダー入力とする、Teacher Forcingという手法
こちらは、推論時の分布と訓練時の分布が異なるという問題がある。
誤差が連鎖的に大きくなる問題に対応するために、
一つ前の時刻のターゲットをデコーダー入力とする、Teacher Forcingという手法
こちらは、推論時の分布と訓練時の分布が異なるという問題がある。
参考文献レポート
認定テストにおいて、BLEUの演算に関する問題が出たのでまとめる
$$ \mathrm{BLEU}=\mathrm{BP} \cdot \exp \left(\sum_{n=1}^N w_n \log p_n\right) $$
※対数荷重平均なのは、nが大きくなるほどスコアが指数的に高くなることを防ぐため
$$Brevity Penalty = exp(1-\frac{r}{c})$$ r:参照文の長さ c:候補文の長さ
このペナルティは、候補文が単に短いためにmodified precisionが高くなり、BLEUが高くなることを防ぐために導入された 参考:“https://blog.pangeanic.com/ensuring-good-machine-translation-using-bleu-scoring"
modified n-gram precision あるngramトークンの候補文における出現回数をCount, 参照訳ごとの出現回数のうち最大値をMax_Ref_Countとして
$$ Count_{clip}=\min (\text { Count }, max_Ref_Count) $$
$$ p_n = \frac{\sum_{\text {n-gram } \in C} \operatorname{Count}{\text {clip }}(\mathrm{n} \text {-gram })}{\sum{\mathrm{n} \text {-gram } \in C} \operatorname{Count}(\mathrm{n} \text {-gram })} $$
参考:“https://nryotaro.dev/posts/bleu/"
BERT
Bidirectional Transformers
背景
自然言語処理タスクは事前学習が有効
文レベルのタスク:文同士の関係が重要 文章類似度 言い換え表現 トークンレベル:モデルはトークンレベルで良い出力が要求される
事前学習のアプローチ
- Feature Based
- N-gram モデル (1992)
- Word2Vec(2013)
- ELMo(2017,2018)
- Context sensitiveな素性を抽出
- 既存の素性にConcatして使用することで複数のNLPタスクでSOTAを達成
- Fine Tuning:モデルはそこまで巨大ではないのでFine Tuningも現実的な速度で実行可能
双方向Transformer
転移学習で8つのタスクでSOTAを達成
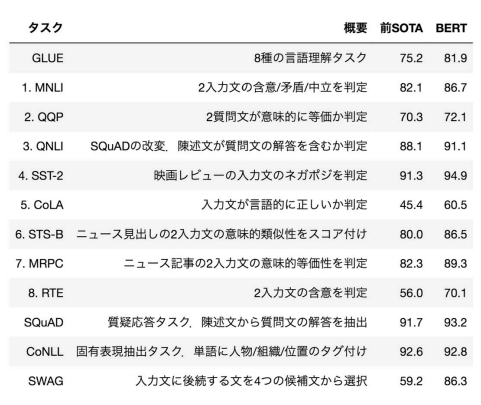 (講義スライドより引用)
(講義スライドより引用)
特徴
入力表現
- 文章のペア または 文章単体
- 単語ベクトルの系列
- WordPieceでTokenizeしたToken Embeding
- TransformerでもあったPosition Embeding (Positional Encoding)
- 文章のペアを考慮したSegment Embeding
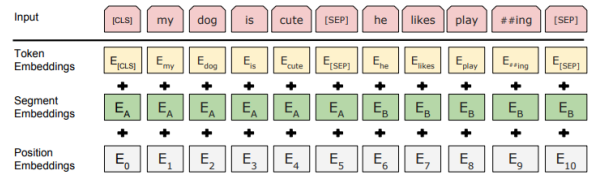 (講義スライドより引用)
(講義スライドより引用)
事前学習タスク
- マスク単語予測タスク:入力系列のうち15%がMASK対象に選ばれてフラグが付与される。そのうち80%をMASKトークン、10%がランダムな他の単語、10%はそのままにして、フラグがついている位置の単語がなにか予測する
- 通常の言語モデルの同時確率=条件付き確率の時系列での総乗が未来の情報のリークによって使えない →CBOW(continuous bag-of-words)の考え方を使う
$$L = - \frac{1}{M}\underset{i\in{Mask}}{\sum} log P(w_i|W\lnot _{j\in{Mask}})$$
- 隣接文判定タスク:2つの連なる文章ペアに対して、隣接文を50%の確率でシャッフル→入力された2つの文章が隣接文かの判定をおこなう
汎用モデルとしてのBERT
見る出力の箇所を変えることで、複数のタスクに対応することが可能
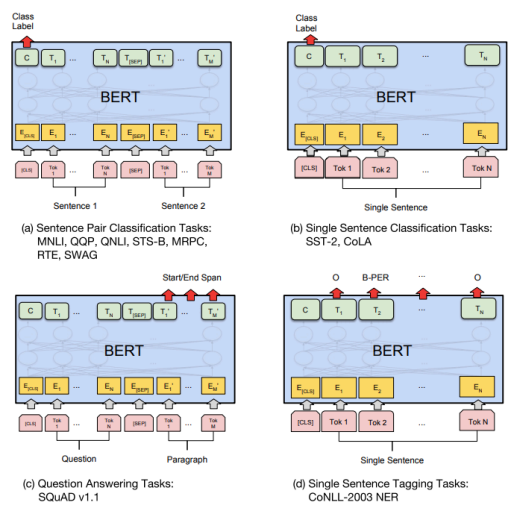 (講義スライドより引用)
(講義スライドより引用)
参考文献レポート
黒本P326 にBERTに関する問題があった。 BERTの構成に関する問題、系列長文並列に並んだTransformer Encoderに前の層のノードすべてが結合している構造がBERTのモノ、系列的に未来の方向のみにつなげているのがOpen AI GPT、LSTMを使っているものがELMO、
事前学習タスクはマスク単語予測、隣接文予測の教師無し学習、再学習については教師あり学習 Positional Encodingに関しても問題として取り上げられていた。
GPT(Generative Pre-Training)
2019 年にOpenAIが開発した事前学習モデル →汎用特徴量を学習済みなため、転移学習に使用可能 特定タスクのためのデータセットが小規模でも、高精度な予測モデルを実現できる 転用の際には、主に下層のファインチューニングを行う(GPT-3以降はファインチューニングしない) モデル構造は変えないことが多い オープンソースが存在する
GPT-2→GPT-3→GPT-4 と後継モデルがある
基本構造はTransformerで ある単語の次に来る単語を予測して文章を完成できるように教師なし学習を行う 入力:単語系列 出力:次に来る単語の確率
学習前のパラメータはランダム値
スペック
GPT-1: 117 million parameters GPT-2: 1.5 billion parameters GPT-3: 175 billion parameters GPT-4: 170 trillion parameters
GPT-4においては入力系列長が25000単語(GPT-3の8倍)まで拡張され、 画像入力も可能になったMulti Modalモデルになっているのが大きなアップデート NNの記憶機能としては、8,000→64000単語
各種試験において、GPT3系よりも大幅に改善された結果を残している
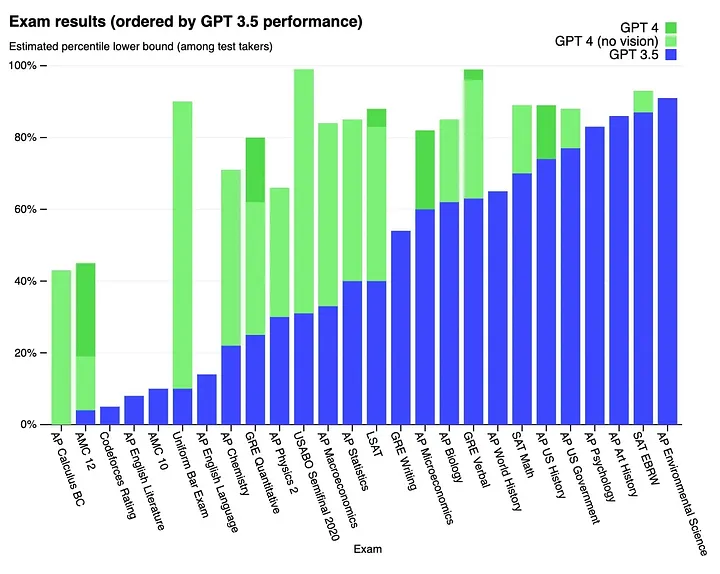 (※2より引用)
(※2より引用)
問題点
- フェイクニュースなどの悪用問題
- GPT-4においては、兵器作成、犯罪などに関するプロンプトへの制限が入っている
- まだ精度がでていない分野もある、物理現象に対する推論や慣習・常識に依存する質問回答など
- 計算リソースの問題:膨大なパラメータが存在するため、事前学習を現実的に実行するために非常に高性能なGPUを要求
学習
GPT-4においては、ライセンスを持つコーパスに加えて、インターネット上のデータを用いている。 インターネット上のデータを用いることで、返答が多岐に渡ってユーザー意図から離れた回答をするのを防ぐためにReinforcement Learning with Human Feedback(RLHF)を導入している
目的関数
言語モデルの最尤推定を行う →同時確率=時系列の条件付き確率の総乗 の 対数を取って、尤度を最大化するパラメータΘを求める。 コンテキストウィンドウ(サイズをkとする)で次の単語を予測する際に見る過去の系列の範囲を定める
$$L(U;\Theta) = \sum log P(u_i|u_{i-k},\dots,u_{i-1};\Theta)$$
ネットワークの演算
- 次の単語を予測するためのコンテキストウィンドウ分の単語系列UをWeで単語ベクトル空間に埋め込み、位置エンコーディングを付加する
$$h_0 = UW_e + W_p$$ 2. 層数分のTransformerのデコードを実行する
$$h_l = transformer_block(h_{l-1}) \forall l \in [1,n]$$ 3. 単語ベクトル空間から系列の次元に戻した後にSoftmax関数で確率の値に変換
$$P(u) = softmax(h_nW_e^T)$$
学習タスク別の入力系列整形と出力表現の変更
下図に示すように、タスクによって、入力系列に予約済みのTokenを付加したり、Transformerの後の線形結合の取り方を変更する
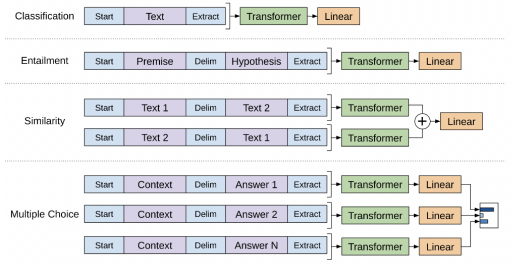 (タスク別のBERT入出力:講義スライドより引用)
(タスク別のBERT入出力:講義スライドより引用)
推論時のPrompt方法
- zero-shot:タスクを指定した後、すぐ推論させる
- one-shot:タスクを指定した後、一つ例を与えて推論させる
- few-shot:タスクを指定した後、複数例を与えて推論させる
BERTとの比較
| モデル | 使用するTransformer | 方向 | Fine Tuning |
|---|---|---|---|
| BERT | エンコーダー | 双方向 | 必要 |
| GPT | デコーダー | 単方向 | GPT-3以降は不要 |
参考文献レポート
GPT-4が現在最新バージョンだったため、講義内容まとめにタスクに対する成績やパラメータ数などGPT-4の内容を調べて記載した
※1:GPT-4 “https://openai.com/gpt-4" ※2:[2303.08774] GPT-4 Technical Report“https://arxiv.org/abs/2303.08774" ※3:The Ultimate Guide to GPT-4 Parameters: Everything You Need to Know about NLP’s Game-Changer | by Mohammed Lubbad | Medium“https://medium.com/@mlubbad/the-ultimate-guide-to-gpt-4-parameters-everything-you-need-to-know-about-nlps-game-changer-109b8767855a"
音声認識
音のデータとしての表現
- 振幅
- 周波数
音データの処理
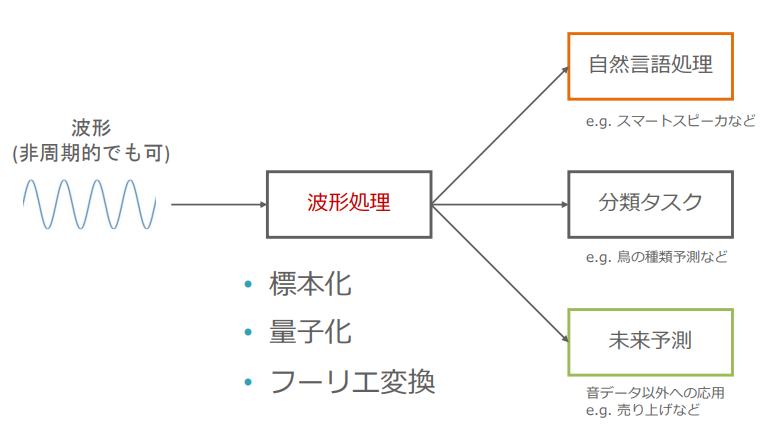 (波形データ処理の概念図:講義スライドより引用)
(波形データ処理の概念図:講義スライドより引用)
- 標本化:アナログ信号をサンプリング周波数にしたがってサンプリングしてデジタル信号に変換する
- サンプリングの法則:周波数hのアナログ信号をサンプリングするには最低でも2倍のサンプリング周波数として2hが必要
- 量子化:連続値を近い離散値に変換する
- フーリエ変換:時系列データを周波数領域のデータに変換する
フーリエ変換
フーリエ変換
関数の級数展開とオイラーの公式と三角関数の直交性から、各周波数成分の大きさを抽出する操作であることがわかる
$$\hat{f}(\omega) = \int_{-\infty}^{\infty} f(t) e^{-i\omega t} , dt$$
- 周波数領域の関数の微分は-iω倍になる
- 畳み込んだ関数のフーリエ変換はフーリエ変換した関数の積に等しい、関数の積のフーリエ変換はフーリエ変換された関数の畳み込みに等しい
フーリエ逆変換
$$f(t) = \dfrac{1}{2\pi} \int_{-\infty}^{\infty} \hat{f}(\omega) e^{i\omega t} , d\omega$$
DFTとFFT
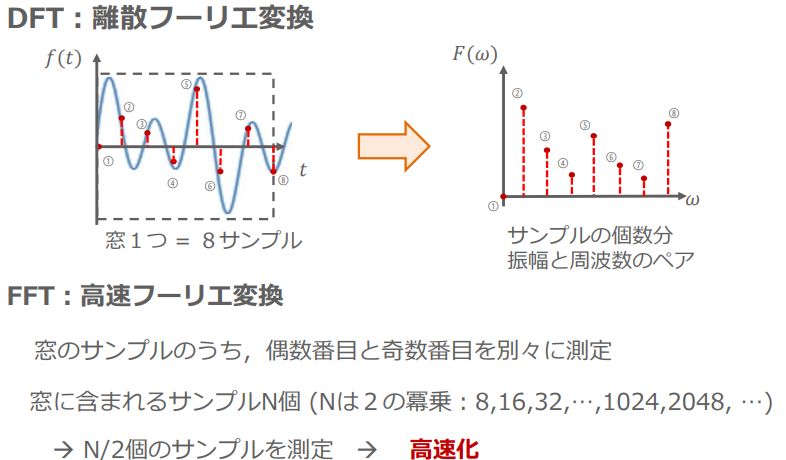 (フーリエ変換の応用例:講義スライドより引用)
(フーリエ変換の応用例:講義スライドより引用)
スペクトル
周期的関数→離散スペクトル 非周期的関数→連続スペクトル
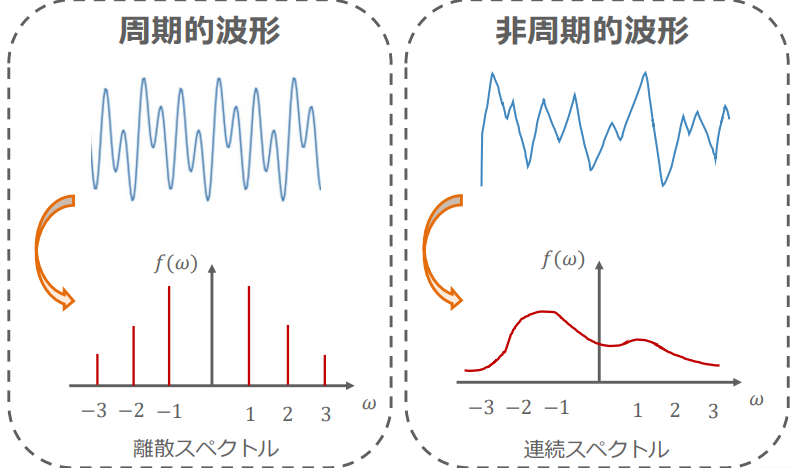 (周期的関数と非周期的関数の周波数領域変換結果の比較:講義スライドより引用)
(周期的関数と非周期的関数の周波数領域変換結果の比較:講義スライドより引用)
スペクトログラム
現実的な非周期音声データを窓関数(特定の時間区間で波形を区切る関数)
窓を少しずつずらしたときのスペクトルをまとめたものをスペクトログラムという
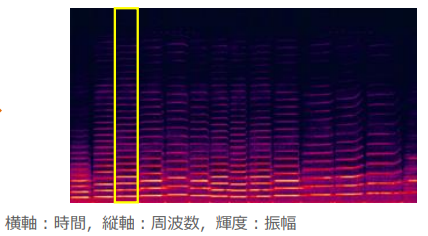 (スペクトログラムの例:講義スライドより引用)
(スペクトログラムの例:講義スライドより引用)
窓関数
元の関数f(t)と窓関数w(t)をつかって新しく周期的な関数g(t)を作成する
$$g(t) = w_i(t)\times f(t)$$
このとき一番カンタンな窓関数は矩形窓で着目する領域が1でそれ以外が0のステップ関数だが下に示す様に
窓1つを取ったときに周期の整数倍で終わっていないと、不連続な点が生まれて、スペクトルに不要な周波数が現れる
(参考:窓関数は周波数特性を調べて使い分ける![サンプルコードあり] - 大学の知識で学ぶ電気電子工学“https://daigakudenki.com/windowing/" )
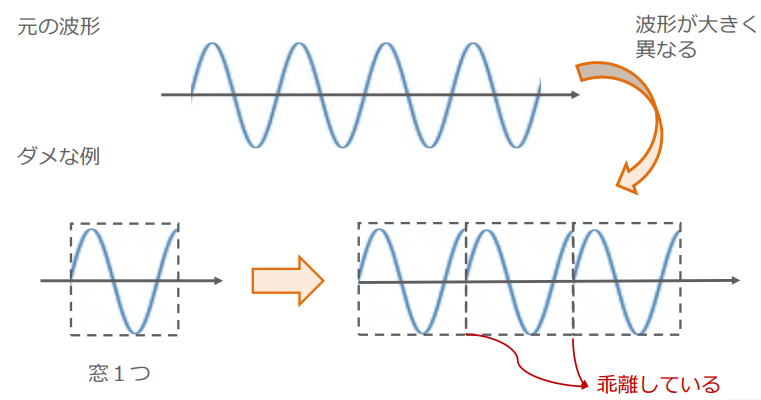 (窓関数に関する問題提起:講義スライドより引用)
(窓関数に関する問題提起:講義スライドより引用)
窓関数を使用する対象の非周期関数は周期が明確ではないので、
窓関数の方で周期的な関数になるように調整する必要がある
そのためによく使われるのがハミング窓
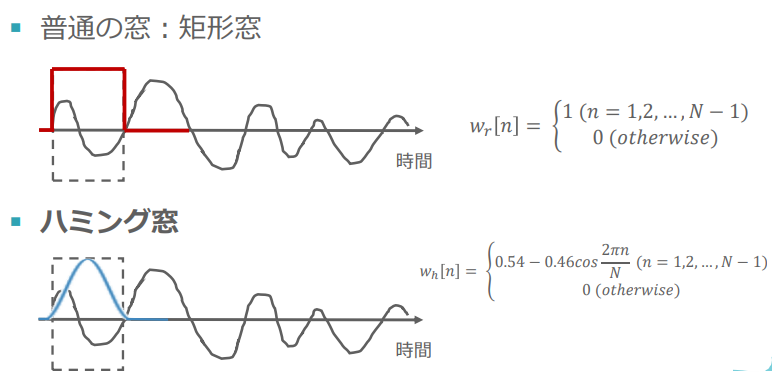 (窓関数の例:講義スライドより引用)
(窓関数の例:講義スライドより引用)
関数の積のフーリエ変換→フーリエ変換した関数の畳み込みにより、 元の関数のスペクトルより均されたスペクトルが得られることになる
そこで窓関数が満たすべき特徴として以下の2つが上げられる
- 周波数分解能が高い
- ダイナミックレンジが低い
音声認識に関する特徴量
- メル尺度:人間の認知特性に応じた分解能に周波数の表現を変える、低周波の感度を上げ(分解能を上げる)て高周波の感度を下げる
- ケプストラム:フーリエ変換した後に対数を取ってフーリエ逆変換を行う
参考文献レポート
ケプストラムというのが何なのか分からなかったため、調査した。 人間の発生特性を考慮して、声帯振動と声道調音の成分を分離して解析できる特徴量とのこと。 参考:水田真理子, 羽地敏明, 阿部千鶴子, 「ケプストラム音響分析の有用性」, 日本言語聴覚医学会雑誌, 第62巻, 第3号, pp. 186-194, 2021. “https://www.jstage.jst.go.jp/article/jjlp/62/3/62_186/_pdf”
窓関数の項目で、不連続になるのがなぜ問題なのかの調査を行った。 ”””(再掲) 窓1つを取ったときに周期の整数倍で終わっていないと、不連続な点が生まれて、スペクトルに不要な周波数が現れる (参考:窓関数は周波数特性を調べて使い分ける![サンプルコードあり] - 大学の知識で学ぶ電気電子工学“https://daigakudenki.com/windowing/" ) ”””
CTC(Connectionist Temporal Classification)
従来の音声認識モデルの概略
 (従来の音声認識モデルの概略:講義資料より引用)
(従来の音声認識モデルの概略:講義資料より引用)
- 音響モデル 音声特徴量と音素列の間の確率を計算するモデル 音素とは、/a/や/i/といった母音、/k/や/s/といった子音から構成される音の最小単位 隠れマルコフモデル+混合正規分布→隠れマルコフモデル+DNNとなることで飛躍的にせいどが向上した
- 発音辞書 音素列と単語との対応を扱うモデル
- 言語モデル 自然言語処理と同様にこれまでの系列入力からある単語が得られる確率を求める
CTCの概略
End-to-Endでの学習 を行うRNNを用いた音声認識モデル ステップバイステップで学習するモデルに比べて構成がシンプルで実装がし易いメリットがある
重要な発明
- ブランクラベルの導入
- forward-backward algorythmを用いたDNNの学習
ブランクラベルの導入
目的
- 連続する同一ラベルの入力を表現する
- ポーズのときに不自然なラベルを与えることを避ける
フレーム単位の入力系列から最終的なテキスト系列までの変換
- RNNで各音素の確率から最大のか確率を持つものを取得する
- 縮約 (以降 関数Bとする)
- 連続して出現している同一ラベルを 1 つのラベルにまとめる
- ブランク「−」を削除する
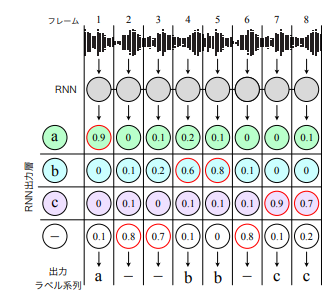
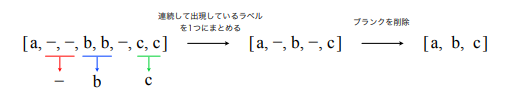 (入力からテキスト系列出力まで:講義資料より引用)
(入力からテキスト系列出力まで:講義資料より引用)
B(a, −, −, b, b, −, c, c) = a, b, c
forward-backward algorythmを用いたRNNの学習
目的関数
正解テキスト系列$l^\star$、入力系列$x$としたときの$P(l^\star|x)$が最大となるパラメータを求める
$$ \begin{aligned} P(\boldsymbol{l^\star} \mid \boldsymbol{x}) & =P([\mathrm{a},-, \mathrm{b}, \mathrm{b}, \mathrm{b}, \mathrm{c},-,-] \mid \boldsymbol{x})+P([-,-, \mathrm{a},-, \mathrm{b}, \mathrm{b},-, \mathrm{c}] \mid \boldsymbol{x})+\cdots \ & =\sum_{\boldsymbol{\pi} \in \mathcal{B}^{-1}(\boldsymbol{l^\star})} P(\boldsymbol{\pi} \mid \boldsymbol{x}) \end{aligned} $$
$P(l^\star|x)$は上に示す様に、縮約して$l^\star$になる入力系列の確率をすべて足し合わせたものになる。 各パターンの確率は各ラベルの得られる確率$y_k^t$(kはラベル、tはフレーム)の総乗になるので
$$ P\left(\boldsymbol{l}^* \mid \boldsymbol{x}\right)=\sum_{\boldsymbol{\pi} \in \mathcal{B}^{-1}\left(\boldsymbol{l}^\right)} P(\boldsymbol{\pi} \mid \boldsymbol{x})=\sum_{\pi \in \mathcal{B}^{-1}\left(\boldsymbol{l}^\right)} \prod_{t=1}^T y_{\pi_t}^t $$
損失関数としては
$$ L_{CTC} = - log P(l^\star|x) $$
効率的な計算のためのforward-backward algorythm
問題意識:$P(l^\star|x)$を算出する際に愚直に行うのは効率が悪い
- 排反な事象への分類:特定のフレームにおいて特定のラベルを通って正解テキスト$l^\star$に縮約したときになる確率を考える ($l^\prime$は$l^\star$の各ラベルの間にブランクを挿入したラベル系列) $$\left.P\left(\boldsymbol{l}^* \mid \boldsymbol{x}\right)=\sum_{s=1}^{\left|\boldsymbol{l}^{\prime}\right|} \underbrace{\sum_{\substack{\boldsymbol{\pi} \in \mathcal{B}^{-1}\left(\boldsymbol{l}^*\right), \pi_t=l_s^{\prime}}} P(\boldsymbol{\pi} \mid \boldsymbol{x})}_{\text{※1:特定フレームに着目した排反事象の確率の和}} \quad \right.\text{ (for any t )}$$
- 前向き確率、後ろ向き確率を使って※1の値を表現する
(以下の数式中の[]はガウス記号で、その値を超えない最大の整数を示す。ベクトルの下付き文字a:bは成分a~bまでの要素を持つベクトルを示す)
- 前向き確率 $\alpha_t(s)$ 始点からフレーム $t$ 、拡張ラベル $s$ の頂点に到達するまでの全パスの確率の総和
$$ \alpha_t(s) \equiv \sum_{\mathcal{B}\left(\pi_{1: t}\right)=l_{1:[s / 2]}^*} \prod_{t^{\prime}=1}^t y_{\pi_{t^{\prime}}}^{t^{\prime}} $$
- 後ろ向き確率 $\beta_t(s)$
フレーム $t$ 、拡張ラベル $s$ の頂点から終点まで到達する全パスの確率の総和
$$ \beta_t(s) \equiv \sum_{\mathcal{B}\left(\pi_{t: T}\right)=l_{[s / 2]: l^* \mid}} \prod_{t^{\prime}=t}^T y_{t_{t^{\prime}}}^{t^{\prime}} $$ $$ \begin{aligned} \alpha_t(s) \beta_t(s) &=\left(\sum_{\mathcal{B}\left(\pi_{1: t}\right)=l_{1:[s / 2]}^} \prod_{t^{\prime}=1}^t y_{\pi_{t^{\prime}}}^{t^{\prime}}\right)\left(\sum_{\mathcal{B}\left(\pi_{t: T}\right)=l_{[s / 2]: ! l \mid}^} \prod_{t^{\prime}=t}^T y_{\pi_{t^{\prime}}}^{t^{\prime}}\right) \ &=\sum_{\mathcal{B}\left(\rho_{1: t}\right)=l_{1:[s / 2]}^} \sum_{\mathcal{B}\left(\boldsymbol{\sigma}{t: T}\right)=l{[s / 2]:|l|}^} \prod_{\tau=1}^t y_{\rho_\tau}^\tau \prod_{\nu=t}^T y_{\sigma_\nu}^\nu \ & =y_{l_s^{\prime}}^t \sum_{\pi \in \mathcal{B}^{-1}\left(l^\right), \Pi_t=l_s^\prime} \prod_{\pi_{t^{\prime}}}^{t^{\prime}}y_{\pi_{t^\prime}}^{t^\prime} \ & =y_{l_s^{\prime}}^t \sum_{\substack{\pi \in \mathcal{B}^{-1}\left(l^\right), \pi_t=l_s^{\prime}}} P(\boldsymbol{\pi} \mid \boldsymbol{x}) \ & \end{aligned} $$ 以上より、前向き確率と後ろ向き確率を用いて、フレームtにおいてラベルsの頂点を通るパスの確率の総和は以下の様に示せる
$$ \sum_{\substack{\pi \in \mathcal{B}^{-1}\left(l^*\right), \pi_t=l_s^{\prime}}} P(\boldsymbol{\pi} \mid \boldsymbol{x}) = \frac{\alpha_t(s) \beta_t(s)}{y_{l_s^\star}^{t}} $$ 3. 前向き確率、後ろ向き確率を再帰計算によって求める 初項についてはブランクか、正解ラベルの1文字目の2通りしか無いので以下の様になる。 $$ \begin{equation}\ a_0(s) = \begin{cases} y_{_}^0 & \text{s=1:ブランク} \ y_{l_{1}^\star}^0 & \text{s=2:正解ラベルの1文字目} \ 0 & \text{else} \end{cases} \end{equation}
$$
それ以降の遷移について考えると下図の様に3通りで
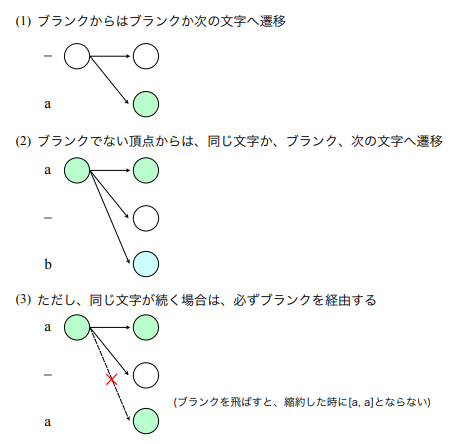 (状態遷移:講義スライドより引用)
(状態遷移:講義スライドより引用)
$$ \alpha_{t+1}(s)= \begin{cases}{\left[\alpha_t(s)+\alpha_t(s-1)\right] y_{l_s^}^{t+1}} & \text { (if } l_s^=\text { blank or } l_{s-2}^=l_s^ \text { ) } \ {\left[\alpha_t(s)+\alpha_t(s-1)+\alpha_t(s-2)\right] y_{l_s^*}^{t+1}} & \text { (otherwise) }\end{cases} $$
後ろ向き確率についても同様
損失関数の誤差逆伝播
出力層の各ノード$y_k^t$に対する損失関数の勾配の計算は、前向き確率及び、後ろ向き確率を用いて以下の様になる。
$$ \begin{aligned} \frac{\partial \mathcal{L}{\mathrm{CTC}}}{\partial y_k^t} & =-\frac{1}{P\left(\boldsymbol{l}^* \mid \boldsymbol{x}\right)} \frac{\partial P\left(\boldsymbol{l}^* \mid \boldsymbol{x}\right)}{\partial y_k^t} \ & =-\frac{1}{P\left(\boldsymbol{l}^* \mid \boldsymbol{x}\right)} \frac{\partial}{\partial y_k^t}\left(\sum{s=1}^{\left|\boldsymbol{l}^\right|} \frac{\alpha_t(s) \beta_t(s)}{y_{l_s^}^t}\right) \ & =-\frac{1}{P\left(\boldsymbol{l}^* \mid \boldsymbol{x}\right)}\left(-\sum_{s \in \operatorname{lab}\left(\boldsymbol{l}^, k\right)} \frac{\alpha_t(s) \beta_t(s)}{\left(y_{l_s^}^t\right)^2}\right) \ & =\frac{1}{P\left(\boldsymbol{l}^* \mid \boldsymbol{x}\right)} \frac{1}{\left(y_k^t\right)^2} \sum_{s \in \operatorname{lab}\left(l^*, k\right)} \alpha_t(s) \beta_t(s) \end{aligned} $$
推論の実行
best path decoding:各フレームで最も確率の高いラベルのみを通るパスに着目して、そのパスを縮約して得られるテキスト系列を認識結果として出力する
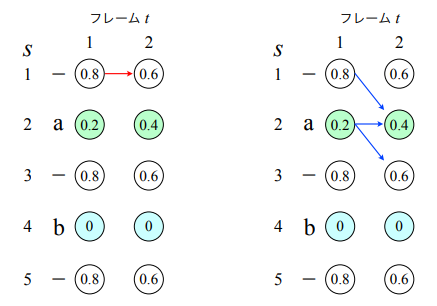 (推論時の動作と問題点:講義スライドより引用)
(推論時の動作と問題点:講義スライドより引用)
上の例では左の赤い矢印で示した(s, t) = (1, 1) → (1, 2) というパスが best path このときB(-,-) =ラベルなし、確率は 0.8 × 0.6 = 0.48
次に右の青い矢印で示した$B(\pi) = [a]$となる経路を考えると、 確率の総和は0.2 × 0.4 + 0.2 × 0.6 + 0.8 × 0.4 = 0.52となり、best pathより大きい
この様に必ずしもbest pathが一番高い確率になるとは限らない問題がある →確率が高い順にいくつかのパスを保持してデコードするbeam search decodingが実践上はよく使われる
DCGAN
GAN
概要
Generator: 乱数からデータを生成
Discriminator:入力データが真のデータか、乱数から生成されたデータかを識別
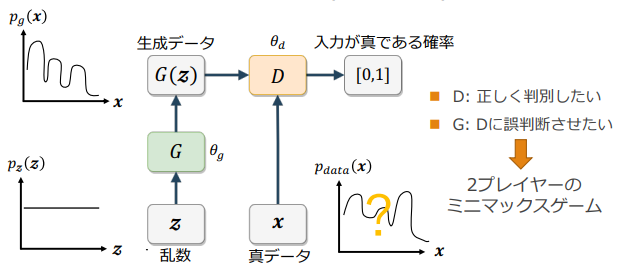 (GANの概念図:講義資料より引用)
(GANの概念図:講義資料より引用)
2player min-max game
一人が自分の勝利する確率を最大化、もうひとりが相手の勝利する確率を最小化する作戦をとる Discriminatorが最大化、Generatorが最小化をする
$$ \begin{gathered} \min G \max D V(D, G) \ V(D, G)=\mathbb{E}{\boldsymbol{x} \sim p{\text {data }}(\boldsymbol{x})}[\log D(\boldsymbol{x})]+\mathbb{E}{\mathbf{z} \sim p{\boldsymbol{z}}(\mathbf{z})}[\log (1-D(G(\mathbf{z})))] \end{gathered} $$
最適化の手順
 (GeneratorとDiscriminatorのパラメータ更新方法:講義スライドより引用)
(GeneratorとDiscriminatorのパラメータ更新方法:講義スライドより引用)
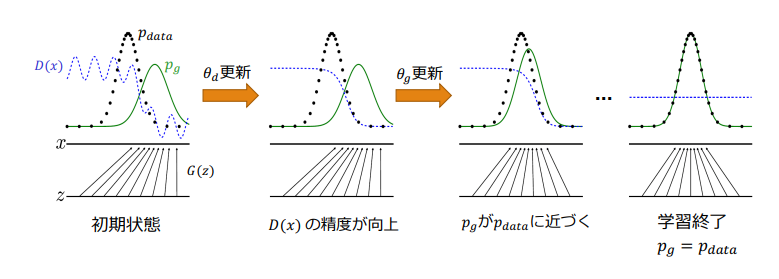 (GANのパラメータ最適化と確率分布の変化:講義スライドより引用)
(GANのパラメータ最適化と確率分布の変化:講義スライドより引用)
Generatorが本物のようなデータを生成できるのはなぜか?
$p_g = p_{data}$のとき、価値関数V(D,G)が最適化されていることを示せば良い
- Gを固定し、価値関数が最大値を取るときのD(x)を算出
- 上記のD(x)を価値関数に代入して、Gが価値関数を最小化する条件を算出
価値関数の最大化
$$ \begin{aligned} & V(D, G)= \mathbb{E}{\boldsymbol{x} \sim p{\text {data }}(\boldsymbol{x})}[\log D(\boldsymbol{x})]+\mathbb{E}{\mathbf{z} \sim p_z(\mathbf{z})}[\log (1-D(G(\mathbf{z})))] \ &= \int{\boldsymbol{x}} p_{\text {data }}(\boldsymbol{x}) \log (D(\boldsymbol{x})) d x+\int_{\boldsymbol{z}} p_z(\mathbf{z}) \log (1-D(G(\mathbf{z}))) d z \ &= \int_{\boldsymbol{x}} p_{\text {data }}(\boldsymbol{x}) \log (D(\boldsymbol{x}))+p_g(\boldsymbol{x}) \log (1-D(\boldsymbol{x})) d x\ \&\text{ここで、}{\mathrm{y}=D(\boldsymbol{x}), a=p_{\text {data }}(\boldsymbol{x}), b=p_g(\boldsymbol{x}) \text { と置けば }} \ \ & a \log (y)+b \log (1-y) \end{aligned} $$
変分問題の公式を考えると、
$$ \mathcal{L}[f] = \int L(x, f(x)) dx $$ 以上のような目的関数があるとき、 この目的関数の停留関数(最大化または最小化を実現する関数)f(x)は以下の方程式を満たす。
$$ \frac{dL(x, f(x))}{df(x)} = 0 $$
以上のことから、y=f(x)とみると $V(D,G) = \int_{\boldsymbol{x}} a \log (y)+b \log (1-y)dx$ なので、$a \log (y)+b \log (1-y)$をyで微分して
$$ \begin{align} &\frac{a}{y}+\frac{b}{1-y}(-1) = 0\ &\frac{a}{y}=\frac{b}{1-y}\ &a-ay = by\ &y = \frac{a}{a+b} \end{align} $$ より,
$$ D^\star(x) = \frac{p_{data}(x)}{p_{data}(x)+p_g(x)} $$
価値関数の最小化
ここまで求めてきた$D^\star(x)$を用いて、価値関数は以下のようになる
$$ \begin{aligned} V & =\mathbb{E}{\boldsymbol{x} \sim p{\text {data }}} \log \left[\frac{p_{\text {data }}(\boldsymbol{x})}{p_{\text {data }}(\boldsymbol{x})+p_g(\boldsymbol{x})}\right]+\mathbb{E}{\boldsymbol{x} \sim p_g} \log \left[1-\frac{p{\text {data }}(\boldsymbol{x})}{p_{\text {data }}(\boldsymbol{x})+p_g(\boldsymbol{x})}\right] \ & =\mathbb{E}{\boldsymbol{x} \sim p{\text {data }}} \log \left[\frac{p_{\text {data }}(\boldsymbol{x})}{p_{\text {data }}(\boldsymbol{x})+p_g(\boldsymbol{x})}\right]+\mathbb{E}{\boldsymbol{x} \sim p_g} \log \left[\frac{p_g}{p{\text {data }}(\boldsymbol{x})+p_g(\boldsymbol{x})}\right] \end{aligned} $$
ここでJSダイバージェンスを思い出すと
$$ JS(p||q) = \frac{1}{2} (\mathbb{E}{x\sim p}log(\frac{2p}{p+q})+\mathbb{E}{x\sim q}log(\frac{2q}{p+q})) $$ なので、 $$ V = 2 \times JS(p_{data}||p_g) - 2log2 $$
JSダイバージェンスは2つの確率分布が一致するときに最小値0を取る非負の値なので
$$ \underset{p_g}{argmin}\quad V = p_{data} $$ $p_g = p_{data}$のとき、最小値が得られる。
DCGANとは
Deep Convolutional GANの略で、いくつかの構造制約を持つ
- Generator :転置畳み込みによって乱数を画像にアップサンプリングする
- Pooling層の代わりに転置畳み込み層を使⽤
- 最終層はtanh、その他はReLU関数で活性化
- Discriminator:畳み込み層により画像から特徴量を抽出し、最終層をsigmoid関数で活性化
- Pooling層の代わりに畳み込み層を使⽤
- Leaky ReLU関数で活性化
- 共通事項
- 中間層に全結合層を使わない
- バッチノーマライゼーションを適⽤
参考文献レポート
黒本P348に該当箇所あり。 2プレイヤーの最適化に関する項目、Discriminatorが目的関数を最大化し、Generatorが最小化する。 どんな工夫がなされたかという項目は、バッチ正規化が生成、識別器ともに使われているというところが問われた
Conditinal GAN
特徴
- GANの入力について、Generator、Discriminatorともにラベル入力が加わる
- 基本的なネットワーク構成はGANと同様
- Discriminatorのラベル識別のパターンが異なる
| 画像入力 | ラベル入力 | Discriminatorの判定 |
|---|---|---|
| Gが生成した犬の画像G(z|y) | yラベル | ☓ |
| Gが生成した犬の画像G(z|y) | y以外のラベル | ☓ |
| 真のラベルyの画像x | yラベル | ◯ |
| 真のラベルyの画像x | y以外のラベル | ☓ |
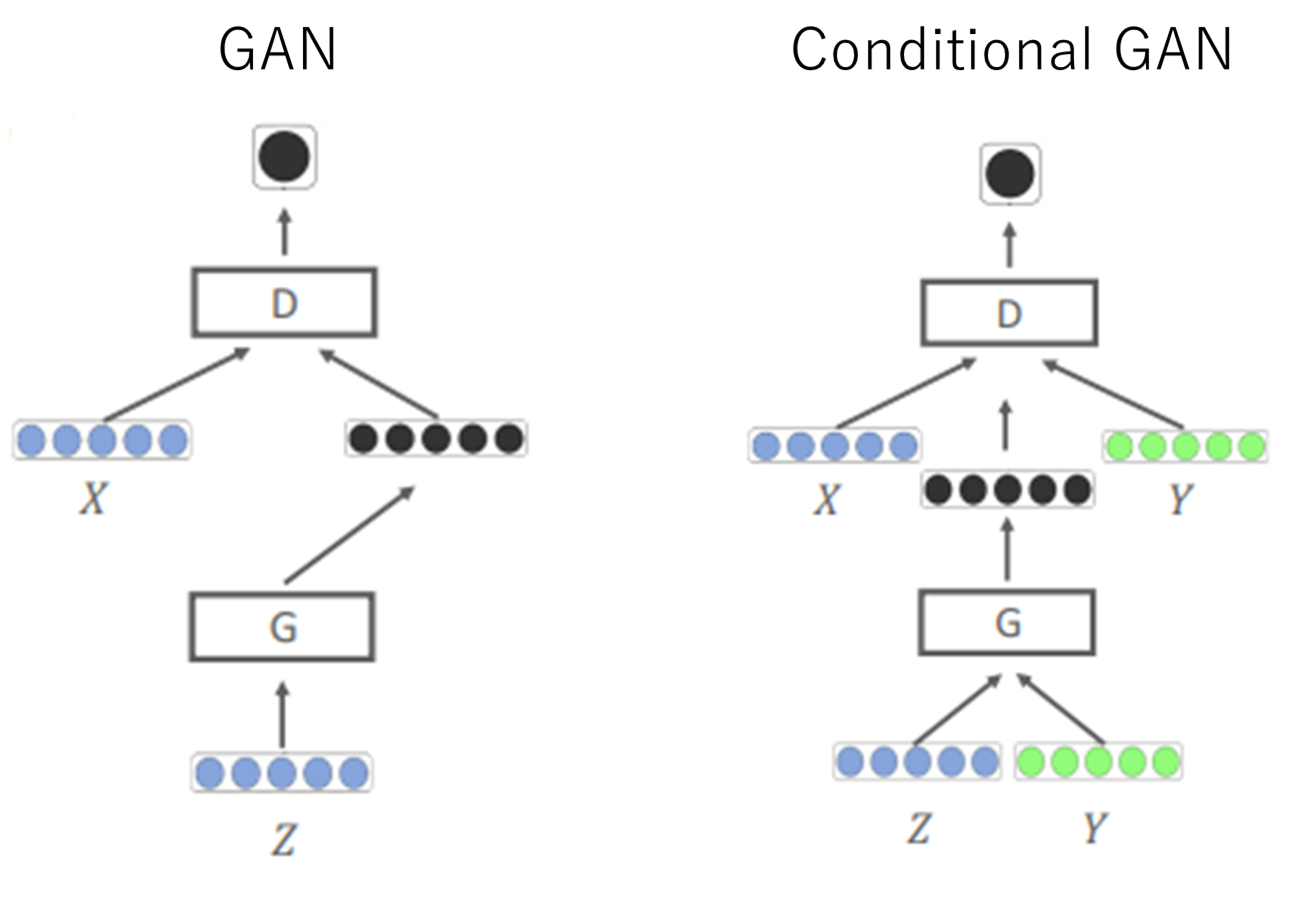 (GANとConditinal GANの入力の比較:講義スライドをもとに作成)
(GANとConditinal GANの入力の比較:講義スライドをもとに作成)
参考文献レポート
黒本P348に該当箇所あり。 生成器、識別器への入力に関する内容が問われた。
Pix2Pix
簡単にいうと、画像をラベルに変換にした後にConditional GANを実行するようなモノ
条件画像を入力→何らかの変換処理を行った画像を出力
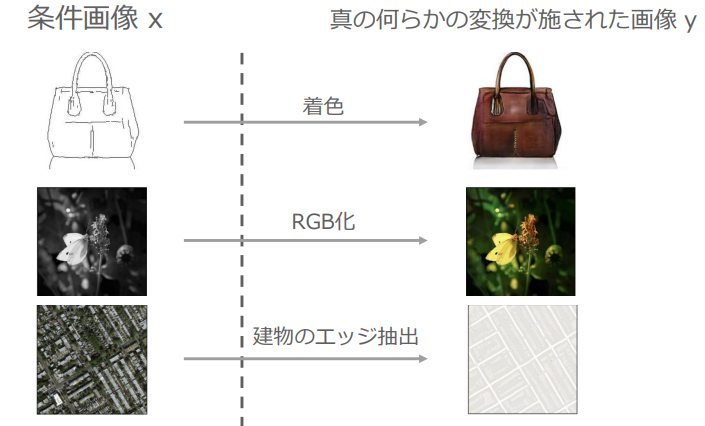 (Pix2Pixの動作イメージ:講義資料より引用)
(Pix2Pixの動作イメージ:講義資料より引用)
工夫
- UNetを利用 →物体の位置情報を伝達できる →入出力のサイズが一致 →ピクセル単位での変換が可能
- L1正則化(Generatorに追加)
→視覚的一致性を高める
→画像の高周波成分を学習してぼやけることが防げる
 (Pix2PixでのL1正則化の効果:講義資料より引用)
(Pix2PixでのL1正則化の効果:講義資料より引用) - PatchGAN:条件画像をパッチに分けて各パッチにPix2Pixを適用 →正確な高周波成分の強調による視覚的一致性の向上 →L1正則化の効果を向上
参考文献レポート
黒本P348,351に該当箇所あり。 Pix2Pixの目的関数に入力と生成画像のL1ノルムを追加することで、画像の大域的な特徴を捉えられる様になったとのこと。
Pix2Pixには画像ペアが必要、Cycle GANとの区別が問われた。
L1,L2損失では捉えられない高周波成分(細かい構造)を捉えるために局所的なパッチ構造に注意をむける PatchGANについての内容。
L1損失のほうがL2損失よりぼかす効果が小さい。
Pix2Pixの生成器でUNetを使う効果はエッジ位置の共有。
A3C (Asynchronous Advantage Actor-Critic)
概要
強化学習の学習手法の一つで 複数のエージェントが同一の環境で非同期的に学習する
- Asynchoronous:非同期な並列学習 →学習の高速化:非同期処理で時間効率が上がる →学習を安定化:同じ状態から始まって、同じ方策に基づいて行動することで生じていた経験の自己相関という強化学習の課題を、複数エージェントを並列で学習させることで低減した
- Advantage:複数ステップ先を考慮して更新する
- Actor:方策によって行動を選択
- Critic:状態価値関数に応じて方策を修正
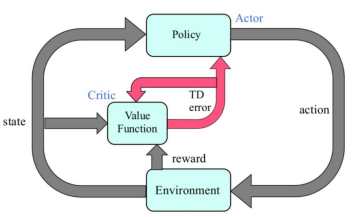 (Actor-Criticの動作イメージ:講義資料より引用)
(Actor-Criticの動作イメージ:講義資料より引用)
DQNではバッファに蓄積した経験をランダムに取り出すことで経験の自己相関を低減したが、 この方法はオフポリシー手法でしか使えない
| オンポリシー | オフポリシー |
|---|---|
| 学習時と実行時に同じ方策を用いる | 学習時と実行時に異なる方策を用いる |
| 方策評価と方策改善を交互に行う | 方策評価と方策改善を同時に行う |
| 例:SARSA, Actor-Critic | 例:Q-Learning, DQN |
非同期学習
- 複数のエージェントが並列で独立にゲーム実行して勾配計算を行う
- 勾配情報でGlobal Networkの重みを更新する
- 定期的にLocal Networkの重みをGlobal Networkの重みと同期する
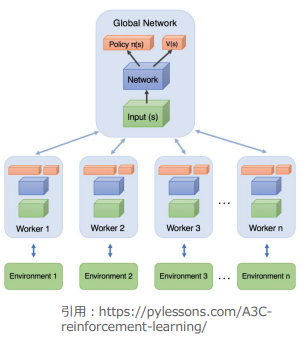 (非同期学習のイメージ:講義スライドより引用)
(非同期学習のイメージ:講義スライドより引用)
損失関数
特徴
- 通常のActor-Criticと異なり、一つの分岐型ネットワークが方策と価値の両方を出力、損失関数も共通
- 数ステップ先まで見たアドバンテージ方策勾配を利用
Total Loss = Advantage方策勾配 + α×価値関数ロス - β×方策エントロピー
Advantage方策勾配
方策勾配法:パラメータΘに基づく方策πに従ったときの期待収益が最大化されるようにΘを最適化する 方策勾配定理により、パラメータ更新に用いられる勾配は以下のように示される ※b(s)はベースライン、行動価値関数から引くことで推定量の分散を小さくして学習の安定化効果がある
$$ \nabla_\theta \rho_\theta=\mathbb{E}\left[\nabla_\theta \log \pi(a \mid s, \theta)\left(Q^{\pi_\theta}(s, a)-b(s)\right)\right] $$ ここで、b(s)の推定には$V_\theta^{\pi_\omega}(s_t)$,価値関数Q(s,a)をアドバンテージ関数としてkステップ先読みした収益をもちいて
$$ \begin{align} &Q(s,a) = (\sum_{i=0}^{k-1}\gamma^i R_{t+i+1})+V_\theta^{\pi_\omega}(s_{t+k})\ &b(s) = V_\theta^{\pi_\omega}(s_t) \end{align} $$
$$ \nabla_\theta \log \pi(a \mid s ; \theta)\left((\sum_{i=0}^{k-1} \gamma^i R_{t+i+1})+V_\theta^{\pi_\omega}\left(s_{t+k}\right)-V_\theta^{\pi_\omega}\left(s_t\right)\right) $$
上記の期待値が方策勾配となる。
方策エントロピー
ランダム性の高い方策にボーナスを与えることで、方策の収束が早すぎて局所解に収束することを防ぐ 方策関数の正則化効果をもつ
$$ -\sum_a \pi\left(a_t \mid s_t\right) \log \pi\left(a_t \mid s_t\right) $$
性能
より短い訓練時間でGPUを使用しなくても高いスコアを実現
 (A3Cの性能比較:講義資料より引用)
(A3Cの性能比較:講義資料より引用)
実装上の制約
- pythonが非同期処理に向いていない
- 並列でネットワークを複数持つ関係上、大規模リソースを持つ環境が必要
→ A2Cという同期処理を行う手法が発表
A2C
- 各エージェントが司令部から行動の指示を受けて1ステップ行動する
- 各エージェントから状態遷移の結果を司令部が受け取って次の指示を行う
Metric-Learning(距離学習)
データ間の距離を学習して、近いデータをクラスタリングしたり、遠いデータを異常値として検知したりする。 深層学習を利用した距離学習を特に深層距離学習と呼ぶ。
深層距離学習
ネットワークの構造自体を変えなくても、類似度を反映した埋め込み空間を構成できるように学習するだけで精度が向上できる
学習の仕方
- 同じクラスに属するサンプルから得られる特徴量ベクトルの距離は近く
- 異なるクラスに属するサンプルから得られる特徴量ベクトルの距離は遠く
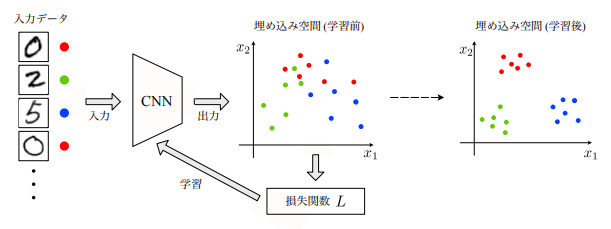 (学習の動作イメージ:講義資料より引用)
(学習の動作イメージ:講義資料より引用)
Siamese network
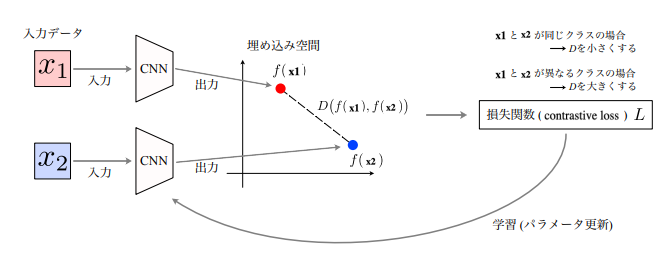 (Siamese Networkの概念図:講義スライドより引用)
(Siamese Networkの概念図:講義スライドより引用)
Contrastive Loss(損失関数)は以下の様に表現される
$$ L=\frac{1}{2}\left[y D^2+(1-y) \max (m-D, 0)^2\right] $$ 各変数は D:埋め込み空間でのデータの距離、ユークリッド距離 y:識別ラベル、2入力が同じクラスのとき1、違うクラスのとき0 m:マージン、どの程度の距離まで罰則項を追加するか
課題
同一クラスと異なるクラスの学習の最適化の不均衡 (異なるクラスの学習は距離がマージンm離れるタイミングで最適化が終了するが、同一クラスは1点に収束するまで終わらない)
Triplet network
Siamese networkの最適化の不均衡を解決するための手法
Siamese networkでは類似クラスと非類似クラスの判定がタスクごとのコンテキストに依存していたが、Triplet networkではアンカークラスを基準に類似度を判定するために、コンテキストを考慮する必要がなくなる
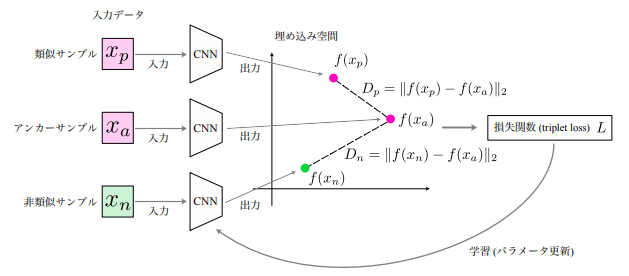 (Triplet Networkの概念図:講義スライドより引用)
(Triplet Networkの概念図:講義スライドより引用)
Siamese networkからの主な変更点
入力データの準備方法が異なる。
- アンカーサンプルを選択する
- アンカーサンプルの類似サンプル(positive sample)と非類似サンプル(negative sample)を一つずつ選択
- 3つの入力データのセットをそれぞれ同一のCNNに入力する
- Triplet Loss(損失関数)を計算 $$ L = max(D_p-D_n+m,0) $$
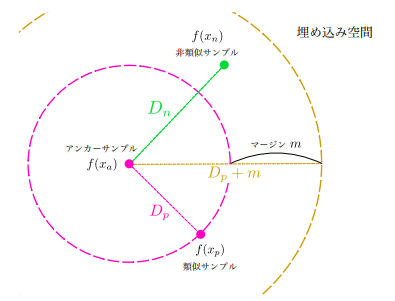 (埋め込み空間における、データサンプルと距離の関係:講義資料より引用)
(埋め込み空間における、データサンプルと距離の関係:講義資料より引用)
課題
- 学習が停滞しやすい
- 学習データセットのサイズが増えると組み合わせが膨大になる
- ほとんどの組み合わせが学習が進むに連れてパラメータ更新に寄与しなくなる →学習に有効な入力セットの厳選(Triplet Selection)が必要になる
- クラス内距離がクラス間距離より近くなることを保証しない
→Quadrupt Lossという4つのデータ点で構成する損失関数が提案、任意のクラス間距離>任意のクラス内距離になる
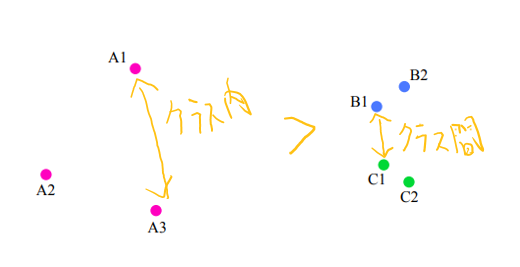 (Triplet Network学習後の埋め込み空間でのクラス別のサンプルの位置の例:講義資料より作成)
(Triplet Network学習後の埋め込み空間でのクラス別のサンプルの位置の例:講義資料より作成)
MAML(メタ学習)
大規模データセット作成の問題点
- アノテーションコスト
- データ収集のハードル →深層学習に用いるデータセットの量を削減したい
既存の対策
- 転移学習
- Fine Tuning →いずれも元のモデルが今回行いたいタスクに適合している重みを持っているとは限らない点が問題
MAMLのコンセプト
- 全タスク集合で共通の重みを学習
- 各タスクでファインチューニングして各モデルの重みを更新
- 各モデルの重みを集めて共通の重みも更新
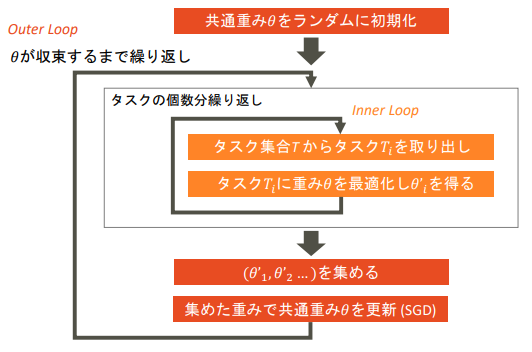 (MAMLの動作フロー:講義資料より引用)
(MAMLの動作フロー:講義資料より引用)
MAMLの課題
タスクごと、共通パラメータの2回の勾配計算が必要 →計算量が多いのが課題 (現実的にInner Loopのステップ数を大きくできない)
MAMLの課題への対策
- First-order MAML: 2次以上の勾配を無視し計算コストを大幅低減
- Reptile: Inner loopの逆伝搬を行わず、学習前後のパラメータの差を利用
GCN(グラフ畳み込み)
CNNは幾何学的なデータにしか使えない
GCNは畳み込み操作をグラフ構造に拡張したもの
活用例:コロナウイルスの感染者数の予測
グラフ
ノードとエッジで構成されるデータ構造 →ネットワーク上のデータのスパース表現、データからネットワーク構造の推定、他分野での複雑データ解析
グラフの例(※1)
- 交通網
- ハイパーリンク
- 電気回路
- 対人関係
- 神経網
- 電力網
- タンパク質・ゲノム構造
- 3Dメッシュ
畳み込みとは
ここでは、重要な部分の抽出と不要な部分の切り捨てを行う操作とする
空間的畳み込み
$$ \begin{align} 連続関数 (fg)(t) &= \int f(\tau)g(t,\tau)d\tau \ 離散関数 (fg)(m)& = \sum_n f(n)g(m,n) \end{align} $$
スペクトル畳み込み
フーリエ変換の性質より、 下の式の様に畳み込みのフーリエ変換はフーリエ変換の積に等しいので、 $$ \mathbb{F}(f*g) = \mathbb{F}(f)\mathbb{F}(g) $$ フーリエ変換した後、特徴的な周波数だけ残すようなフィルタ関数をかけて、再度フーリエ逆変換を行う
Spatial GCN
ノードjの近くにあるノードを以下のように、ノード間の重みが一定以上であるノードとして定義
$$N_\delta(j) = {i \in \Omega: W_{ij}>\delta} $$ これの重心を次の層のノードして扱い、層に分けてクラスタリングを繰り返す
隣接関係(k層における、分割したクラスタ内の要素同士の関係、iは分割したクラスタのi番目の要素)
$$N_k = {N_{k,i};i=1,\dots,d_{k-1}}$$
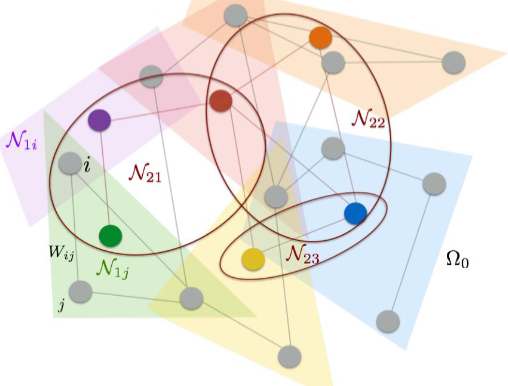 (グラフデータのクラスタリング:講義資料より引用)
(グラフデータのクラスタリング:講義資料より引用)
k層目の出力(k+1層目の入力)は以下の様に書ける
$$ x_{k+1, j}=L_k h\left(\sum_{i=1}^{f_{k-1}} F_{k, i, j} x_{k, i}\right) \quad\left(j=1 \ldots f_k\right) $$
- $L_k$はプーリングの機能
- hは活性化関数
- $F_{k,i}$は隣接関係$N_k$のあるところだけ値をもつスパースな行列
- $f_k$はk層目のフィルタ数
Spectal GCN
フーリエ変換→フィルタ関数を掛ける→逆フーリエ変換
グラフをフーリエ変換するには
フーリエ変換の特徴の、 2回微分したときにもとの関数の定数倍になることに着目する
このとき、2回微分は自分自身と周辺の差を取る操作で行列として表現できる →グラフラプラシアンという値を導入
行列をベクトルにかけた結果がベクトルの定数倍 →固有値・固有ベクトルの関係 →グラフラプラシアンを固有値分解
ここで離散フーリエ変換について、考えると 元の関数に大きさ1の独立した成分の和をとる操作であるため
$$F(t) = \sum f(x) exp(-i\frac{2\pi x}{N})$$ 固有ベクトルと入力ベクトルの内積を取って和をとることに等しい このことから固有ベクトルからなる行列を$\mathbb{Q}$とすると GFT:Graph Fourier Transformは
$$\mathbb{F} = F_G(\vec{f}) = \mathbb{Q}^T\vec{f}$$
グラフラプラシアンが実対称行列であることから、$\mathbb{Q}$は直交行列であり$\mathbb{Q}^{-1} = \mathbb{Q}^T$なので IGFT: Inverse Graph Fourier Transformは
$$F_G^{-1}(\mathbb{F}) = \mathbb{Q}\mathbb{F}$$
グラフラプラシアン
$$ L = D -A $$ L:グラフラプラシアン (実対象行列→固有値ベクトルが直行) D:次数行列 (ノードから何本エッジが伸びているか、対角成分のみを持つ) A:隣接行列 (どのノードに繋がっているか、01の値を持つ対称行列)
GCNの弱点
- Spatial GCN:次元が低く、近傍となる点が限られるため広い範囲で重みを出しにくい
- Spectral GCN:計算量が多く、フィルタが固有基底に依存するためパラメータの使いまわしができない →ChebNetで対応されることで、空間領域にも拡張された
参考
※1:グラフ信号処理〜基礎から応用まで〜“https://speakerdeck.com/ychtanaka/gurahuxin-hao-chu-li-ji-chu-karaying-yong-made?slide=14" 直交ベクトルの線形独立性、正規直交基底、直交行列について解説 | 趣味の大学数学“https://math-fun.net/20201214/7235" 行列の対角化可能性の定義とメリット、例、同値条件について解説 | 趣味の大学数学“https://math-fun.net/20201217/7330/" 対称行列の性質:内積による特徴づけ、逆行列、固有値、対角化について | 趣味の大学数学“https://math-fun.net/20210606/14817/"
Grad-CAM,LIME,SHAP
社会実装を考える際にはモデルの解釈性は重要 →ディープラーニングモデルのブラックボックス性の解消が必要
モデル解釈の手法
- CAM
- Grad-CAM
- LIME
- SHAP
CAM Class Activation Mapping
”Learning Deep Features for Discriminative Localization”という論文において Global Average PoolingがCNNが潜在的に着目している部分を可視化できるようにする役割を持っていることが発見された
利用上の制約
- ネットワークの大部分がCNNで構成されていること
- 出力層の直前でGAPを実行していること
動作イメージ
出力層の重みを特徴マップ上に投影することで画像領域の重要性を識別
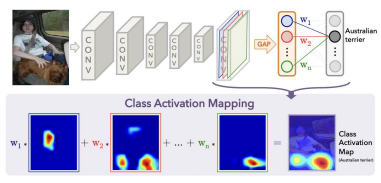 (CAMのコンセプト図:講義資料より引用)
(CAMのコンセプト図:講義資料より引用)
$$ \begin{equation} M_c(x, y)=\sum_k w_k^c f_k(x, y) \end{equation} $$ Mc:クラスCの位置(x,y)の重要度 $w_k^c$:最後の畳み込み層のk番目のフィルタからクラスCにつながる重み $f_k$:最後の畳み込み層のチャンネルのうちk番目の特徴マップ
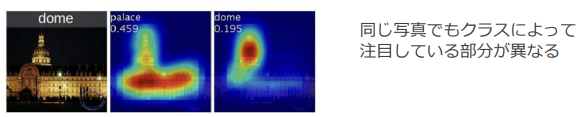 (CAMの出力結果の例:講義スライドより引用)
(CAMの出力結果の例:講義スライドより引用)
CAMの評価
CAMの注目領域にしたがって生成したBounding BoxのLocalizationの指標IoUでの評価が可能
単純にクラス出力から誤差逆伝播で位置を設定した場合よりもGAPを使って、CAMによるBounding Box設定を行ったほうが誤差が小さく出る。
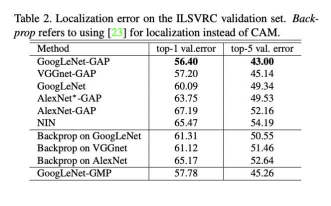 (講義スライドより引用)
(講義スライドより引用)
Grad-CAM
Grad-CAM: Why did you say that? Visual Explanations from Deep Networks via Gradient-based Localization “https://arxiv.org/pdf/1610.02391v1.pdf"
- CNNに判断根拠をもたせ、モデルの予測根拠を可視化する手法
- 最後の畳み込み層の予測クラスの出力値に対する勾配を利用 (勾配が大きい場所は予測クラスの出力に大きく影響する重要な場所という考え方) ※CAMにおいて、特徴マップにGAP-出力層間の重みを使用していたところを勾配で代用している
- GAPがなくても使える、出力がクラスでなくても良いため、様々なタスクで使える
$$ \alpha_k^c=\overbrace{\frac{1}{Z} \sum_i \sum_j}^{\text {global average pooling }} \underbrace{\frac{\partial y^c}{\partial A_{i j}^k}}_{\text {gradients via backprop }} $$
$a_k^c$:クラスCのk番目のフィルタに関する重み係数 $y_c$:クラスCのスコア $A_{ij}^k$:k番目の特徴マップの座標i,jにおける値
ヒートマップの値は以下の様に示される。
$$ L_{c} = ReLU \left( \sum_{k} \alpha_{k}^{c} A^k \right) $$
LIME Local Interpretable Model-agnostic Explanations
“Why Should I Trust You?”: Explaining the Predictions of Any Classifier https://arxiv.org/abs/1602.04938
特定の入力に対する予測に対して、予測根拠を解釈・可視化するツール Ex.)
- 表データ:どの変数が予測に効いたのか
- 画像データ:どの部分が予測に効いたのか
手法
解釈可能なシンプルなモデルで複雑なモデルを近似することで解釈を行う
シンプルなモデルの例
- 決定木
- 線形モデル
近似上の工夫
- 全体ではなく1つの個別の予測結果をLIMEに入力
- 対象サンプル周辺に限ったデータセットを教師データとして、対象範囲内のみで有効なモデルを作成
<複雑な決定境界を持つモデルに対して、太い赤十字で示したデータを説明しようとしたときのLIMEの働きのイメージ>
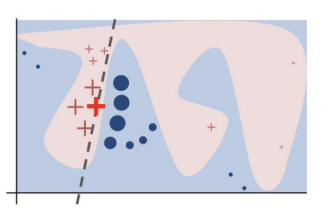 (講義資料より引用)
(講義資料より引用)
目的関数
入力データに対して、元のモデルと近似するモデルの距離に基づく不正確さ(第一項)及び近似モデルの複雑さを示す正則化項(第二項)の和が最小になるような近似モデルgをGから選択する
$$ \xi(x) = \underset{g\in G}{argmin}(L(f,g,\pi_x) + \Omega (g)) $$
近似モデルの入力には、元の入力に摂動を加えたものを用いる 摂動の例
- テキスト:単語のランダム除去
- 画像:スーパーピクセルなどの領域分割に基づくマスク処理
- 表:ランダムに一部のデータを置き換え
$\mathcal{Z}$は説明したいデータ周辺のデータセット、 元の入力zに対して摂動を加えた入力をz’とすると、 $$ \mathcal{L}\left(f, g, \pi_x\right)=\sum_{z, z^{\prime} \in \mathcal{Z}} \pi_x(z)\left(f(z)-g\left(z^{\prime}\right)\right)^2 $$ このとき、$\pi_x(z) = exp(-D(x,z)/\sigma^2)$でσはハイパーパラメータで設定基準が無い問題がある。
解釈例
講義ではテキストをキリスト教、無神論の2クラスに分類するモデルについて LIMEを使って分類時の単語の重要度を可視化した
可視化した結果、どちらのクラスにも関係のない単語が重要であるとされたため データセットを確認したところ、データセットの2割に出現(高頻度)しており、 99%が無神論のクラスに属していた(偏在)
→ データセットのデータ分布の問題があり、作成されたモデルは行いたいタスクに対する汎用性がない
実装時の参考
“https://github.com/marcotcr/lime"
※Pythonを用いた実装ライブラリはデータ形式によってアルゴリズムが異なる
SHAP
A Unified Approach to Interpreting Model Predictions"https://arxiv.org/pdf/1705.07874.pdf”
協力ゲームプレイ理論の概念Shapley Valueを機械学習に応用
Shapley Valueを算出する上での想定:プレイヤーが協力して、それによって獲得した報酬を分配する
Shapley Value
限界貢献度:プレイヤーが一人加入することでどれだけ報酬が増えるか (0人から一人増えるとき、1人から2人になるときなど、元の状態と変化後の状態次第で限界貢献度は異なり、プレイヤーだけの関数にはならない)
参加者の順列分パターンを変更して、各人の限界貢献度を算出して平均をとる。 この平均限界貢献度をShapley Valueという
下図の例では
Aは(4 + 3 + 15 + 15 + 4 + 11) / 6 = 8.7
Bは(6 + 7 + 7 + 15 + 19 + 19) / 6 = 12.2
Cは(25 + 25 + 13 + 5 + 12 + 5) / 6 = 14.2
 (講義スライドより作成)
(講義スライドより作成)
機械学習への応用
| 分野 | 説明 |
|---|---|
| 協力ゲーム理論 | 協力して得た報酬を、貢献度が異なるプレイヤーにどう分配するか |
| 機械学習 | モデルから出力された予測値を、貢献度が異なる特徴量にどう分配するか |
下図に示す様に、協力ゲームでの参加・不参加を特徴量を使用・不使用に置き換えて、予測値の期待値の差を限界貢献度とみなす。
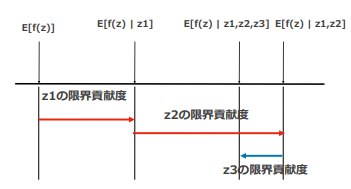 (条件付きの予測値の期待値をつかった機械学習での使用イメージ:講義スライドより引用)
(条件付きの予測値の期待値をつかった機械学習での使用イメージ:講義スライドより引用)
講義での例
ボストンの不動産価格
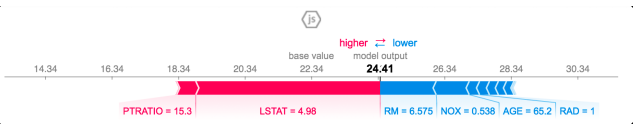 (SHAPによる各特徴量ごとの寄与度の可視化結果:講義スライドより引用)
※値は特徴量でShapley Valueではない
(SHAPによる各特徴量ごとの寄与度の可視化結果:講義スライドより引用)
※値は特徴量でShapley Valueではない
- 寄与度の大きい特徴量を把握する
- その特徴量のデータの分布を確認
- 特徴量の値の評価の仕方についての仮説をたてる
- その特徴量だけを変化させたときのモデル出力の変化をみる
Docker
利用価値
コンテナは仮想マシンに比べて軽量
- 必要最小限のファイル
- 必要最小限のライブラリ
コンテナ型の仮想化
仮想化
効率化
- ハードウェアの数を減らす
- 柔軟なサービス運用
- サービス不可の分散
仮想化の種類
- VM
- 完全VM:OSを仮想化、物理的なOS環境を置き換えられる
- プロセスVM:JAVA VMなどCPUプロセスなどを仮想化するVM プロセス:アプリケーションプログラムの実行単位、実行中のインスタンス
- コンテナ:アプリケーションの仮想化、完全なゲストOSを必要としない ※コンテナ型の仮想化 はVMではない、
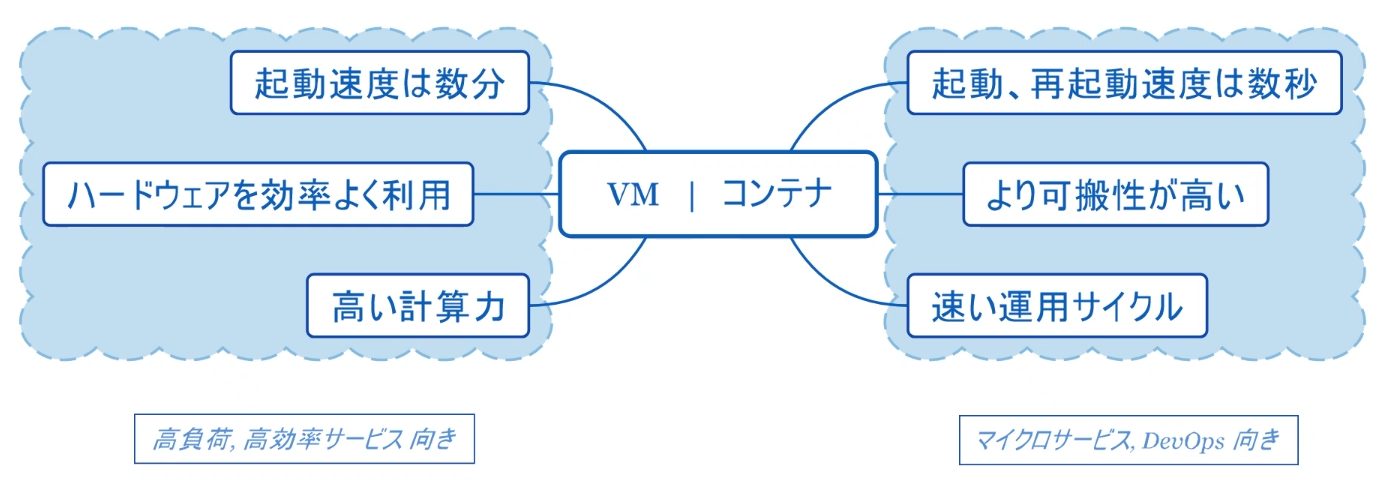
Dockerの仮想化
特徴
Dockerのコンテナは、それぞれ最小限のライブラリと実行ファイルを持ち、 カーネルやハードウェアリソースは共有するので非常に軽量 →起動時間が顕著に高速 →開発サイクルが早くリアルタイム性が求められるWebアプリケーション開発に向く
注意点
- カーネルバージョンのホストOSとコンテナOSの互換性問題
- コンテナOSがLinux → 通常問題にならない
- コンテナOSがLinuxではない → カーネルバージョンの互換性の配慮が必要
- セキュリティ対策 ホストOS上で実行されるユーザプロセスとしてカーネル・ネットワーク・ファイルシステムを共有するため、 論理的隔離度合いが低くなる
Dockerの具体的なオペレーション
Dockerオブジェクト:Dockerコマンドで操作できる対象
- コンテナ
- run/createでイメージからコンテナを生成する
- commitでコンテナの実行内容でimageを更新する
- イメージ
- tagで管理用の名前をつける
- ネットワーク:ボリュームやネットワークを通してリソースの隔離と共有を行う 同一ネットワーク上のコンテナのみが直接通信でき、特にネットワークの名前を指定しない場合はデフォルトのbridgeネットワークにコンテナが追加される
Dockerレジストリによって、 公式イメージを利用したり、自作のイメージの管理ができる
コンテナ自体の保存はできず、
ファイルシステムのみをexportでリソースファイルに抽出して、
イメージに取り込むことができる
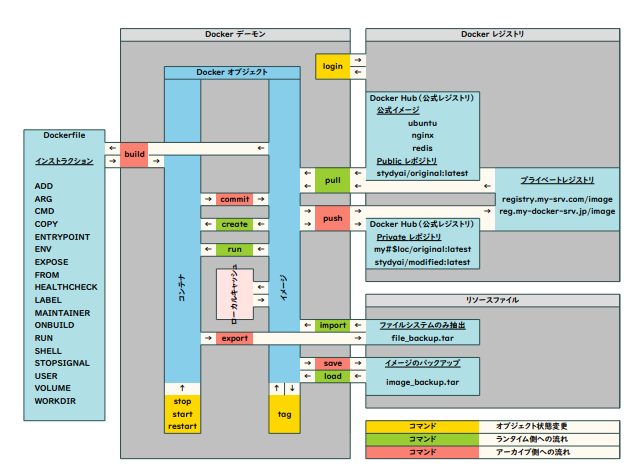 (講義資料より引用)
(講義資料より引用)
Dockerfile
Dockerfileにイメージ作成時の一連の操作
(公式イメージをベースとして取ってくる、必要ライブラリのインストール、ファイルのコピー、作成、ポート指定など)を
Dockerインストラクションを用いて記載する
ビルドは差分キャッシュを行うので、効率的にビルドできる
 (講義資料より引用)
(講義資料より引用)
通信管理
- ホストと通信する:ポートを指定して、コンテナ作成時にバインドする
- ホストの属する物理ネットワークに接続する
- hostドライバで直接接続
- macvlanドライバで、ホスト-VLANインターフェイス上にVLANを構成する必要がある
| ホスト内 | ホスト外 |
|---|---|
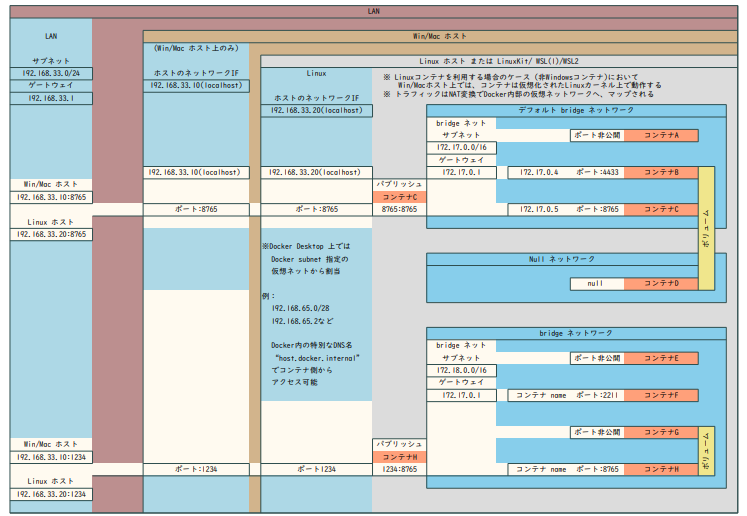 |
 |
docker-compose
サービスの構成や依存関係をyaml形式ファイルにまとめることで複雑なdockerコマンドのオペレーションを整理できる →swarm機能によって提供されるデプロイメントを大幅に簡略化できる
実装演習結果
4_1_transfer-learning.ipynb
- 一般的な処理関連
- クラス数の取得:tensorflow_datasets.データセット.info.features[’label’].num_classesで取得
- 前処理の適用: datset.map(function)メソッド
- ミニバッチでまとめる:datset.batch(BATCH_SIZE)メソッド
- 実行時のデータロードの改善:dataset.prefetch()メソッドで、ステップsの訓練とステップs+1のデータのロードをオーバーラップして実行時間の改善をする
- 転移学習関連
- 定義済みネットワークの利用:tensorflow.keras.applications.モデル.モデルのバージョン()
- 学習済みの重みを使うときは引数weights=“使いたいモデルの名前"にする
- 学習可能にする(FineTuning)にはインスタンスのtrainable属性をTrueにする,事前学習部分を固定したい場合はFalse ※model.layersの各要素ごとにtrainable属性があるので、層ごとに学習するかは選べる
- ネットワークモデルの再構成
model.summary()(必要に応じてtensorflow.keras.utils.plot_model(model))をつかって構造を確認して使用する部分のインデックスを確認して、そこのアウトプットから自分の定義したいモデルのアウトプットを定義
keras.models.Model(inputs,outputs)を利用してモデルを定義
x = DefinedModel.layers[index].output output = keras.layers.使いたいクラス(適切な引数)(x) model = keras.models.Model(inputs=DefinedModel.input,outputs=output)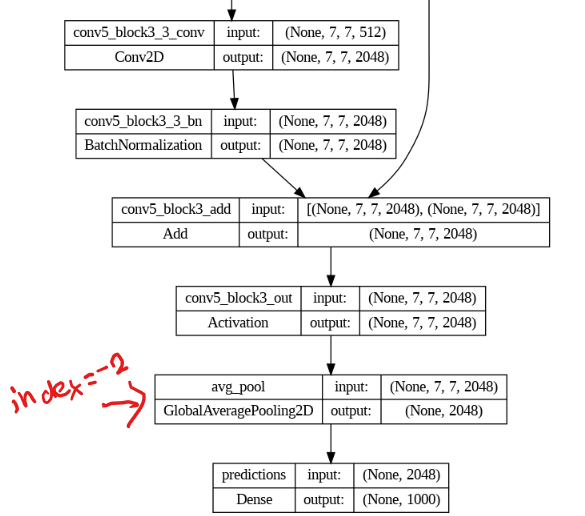
- 定義済みネットワークの利用:tensorflow.keras.applications.モデル.モデルのバージョン()
実行結果と考察
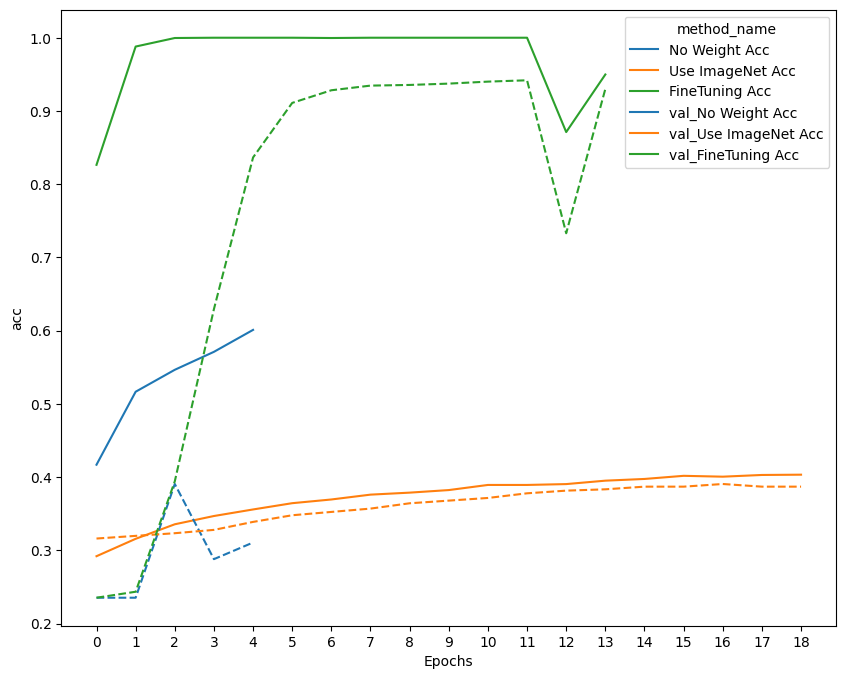
転移学習なしでは、早期に局所最適解に陥ったのか、損失関数の改善が止まって学習が打ち切られてしまった。
転移学習でもとのモデルの重みを固定した場合は、緩やかに改善されたが、正解率は低い
これはImageNetのデータセットが多様な物体を対象としたものに対して、今回利用したFlowerデータセットは花に限って細かく分類するものであるため、事前学習モデルで抽出されている特徴量が合わなかった可能性が考えられる
事前学習モデルの重みの更新も含めたFine Tuningでは正解率は1近くまで改善しており、学習がうまく行っていることがわかる
4_2_wide_resnet.ipynb
4_1と異なり、tf.keras.Sequentialを利用してモデルを再定義、 この場合は、学習済みモデルをtensorflow_hub.KerasLayer(url,trainable)で指定。
FineTuningで重みを再学習する場合も、Batch正規化の平均分散のパラメータは更新されない。
実行結果と考察
パラメータ数と実行時間の比較
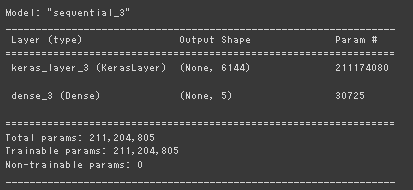
ResNetとWideResNetの学習コストをみたいので、重み固定ではなくFineTuningの結果を載せる 以下に示すように学習可能なパラメータ数はWideResNetで約9倍 (= 211201805/23518277) 実行時間は9.6倍程度(290/30)で言及されていたGPUの特性に合わせた演算での高速化は見られなかった。 ※深層学習のフレームワーク内部で最適化されているのかもしれない
ResNet
| モデルサマリ | 実行結果 |
|---|---|
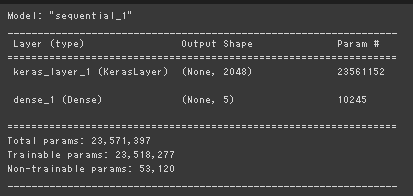 |
 |
Wide ResNet
| モデルサマリ | 実行結果 |
|---|---|
 |
 |
訓練結果の比較
ResNetのFine Tuningの方ではValidationの方の正解率が落ちており、過学習を起こしてしまっていることがわかる Wide ResNetに比べてDropOutがない分、正則化が足りなかったことが原因かと思われる。
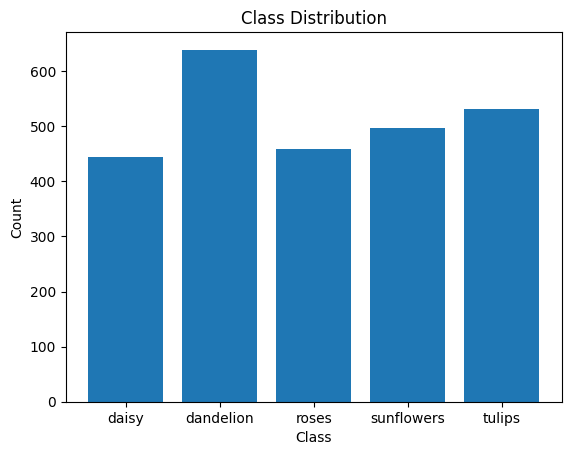
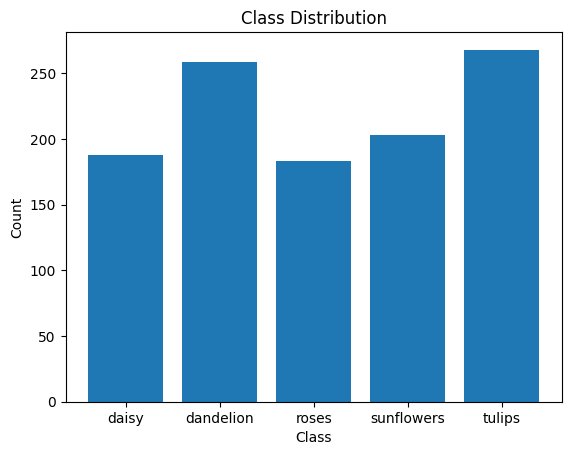
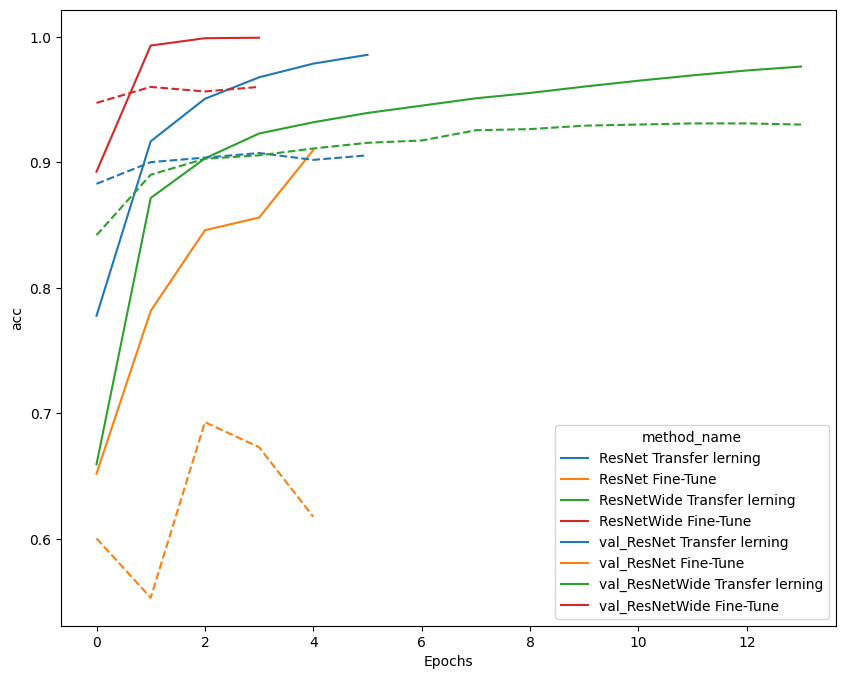 ResNetにも正則化効果のあるBatch Normalizationは入っているので、念のためデータセットのクラス分布が偏っていてDataAugumentationが必要なケースだった可能性も考えたが、そこまで極端な分布になっておらず、テスト、訓練で比較した際も別物の分布とまでは言えないため、バッチサイズが16と小さめに設定されていることが原因では無いかと考えられる。
(Google ColaboratoryのGPU割当制限に引っかかったのか、バッチサイズを上げて検証することはできませんでした。)
ResNetにも正則化効果のあるBatch Normalizationは入っているので、念のためデータセットのクラス分布が偏っていてDataAugumentationが必要なケースだった可能性も考えたが、そこまで極端な分布になっておらず、テスト、訓練で比較した際も別物の分布とまでは言えないため、バッチサイズが16と小さめに設定されていることが原因では無いかと考えられる。
(Google ColaboratoryのGPU割当制限に引っかかったのか、バッチサイズを上げて検証することはできませんでした。)
| 訓練データセットのクラス分布 | テストデータセットのクラス分布 |
|---|---|
 |
 |
4_3_lecture_chap1_exercise_public.ipynb
Pytorchでの実装だったため、実装部分のまとめは省略 一部データ型についてのエラーがあったため、修正をしました。
Seq2Seqの学習テクニックとして、訓練時のDecoderの内部状態の入力にターゲット系列を用いるTeacher Forcingというテクニックがある。 推論時と訓練時でデータの分布が異なるという問題が発生することもあるので、 確率でターゲット系列と前時刻の生成された状態を切り替えて用いるScheduled Samplingという手法がある。
Seq2Seqではデータセット中の入力系列の長さの差分をPaddingで吸収しているので、 損失関数はPadding部分は計算しないようにマスクを掛けたmasked_cross_entropyをもちいる
Loss関数の他に、機械翻訳において一般的なモデル評価指標であるBLEUを計算する。 ※BLEUはn-gram(n個の単語のリスト)のプロが翻訳したリストと予測されたリストのマッチ率に基づく指標
データローダーを実装しないと、メモリに全展開して学習を進めることになり、DeepLearningの規模だとメモリに乗り切らない問題が起こる
実行結果と考察
訓練の経過
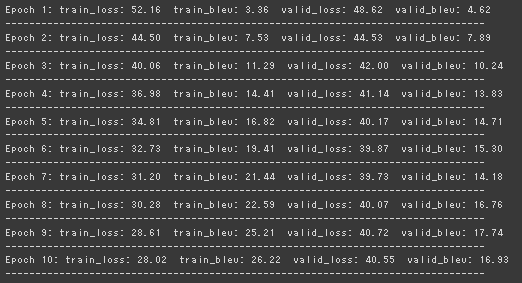
推論結果
 このときBLEU = 17.92904579451379(0~100)
このときBLEU = 17.92904579451379(0~100)
Beam Search を用いたときの結果
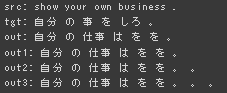
あまりうまく行っていない用に思われる、慣用的な表現は難しかったりするのか、 命令文の構文理解もうまく行ってないことも考えると、コーパスが軽量という話もあったのでそちらの問題も考えられる。
4_5_lecture_chap3_exercise_public.ipynb
tensorflowのバージョン違いの修正
TPU実行周りの設定のバージョン違い修正にかかる時間が読めなかったため、途中で断念。
tensorflow.logging → tensorflow.compat.v1.logging tensorflow.train.Optimizer → tensorflow.keras.optimizers.Optimizer tensorflow.gfile → tensorflow.compat.v1.io.gfile
4_6_bert.ipynb
必要なライブラリをインストールする
日本語の形態素解析にもとづくTokenizeのためのパッケージ郡をインストール
!pip install mecab-python3
!pip install unidic
!python -m unidic download
!pip install fugashi
!pip install ipadic
Transformer関連のネットワークが使えるtransformersライブラリを使用
! pip install transformers
データセットをダウンロード
青空文庫から
!wget https://www.aozora.gr.jp/cards/000148/files/773_ruby_5968.zip
!unzip -O sjjs /content/773_ruby_5968.zip
!wget https://www.aozora.gr.jp/cards/000148/files/56143_ruby_50824.zip
!unzip -O sjjs /content/56143_ruby_50824.zip
!wget https://www.aozora.gr.jp/cards/000148/files/799_ruby_6024.zip
!unzip -O sjjs 799_ruby_6024.zip
文字化けを治す
# nkfコマンドを実行環境にインストール
!apt install nkf
# コマンドを使って文字化けを上書き
!nkf -w --overwrite kokoro.txt sorekara.txt yume_juya.txt
# テキストファイルを一つにまとめる
!cat kokoro.txt sorekara.txt yume_juya.txt > train.txt
transformersから学習済みのTokenizerとモデルを取得する
from transformers import TFBertModel
from transformers import BertJapaneseTokenizer
tokenizer = BertJapaneseTokenizer.from_pretrained('cl-tohoku/bert-base-japanese-whole-word-masking')
bert = TFBertModel.from_pretrained('cl-tohoku/bert-base-japanese-whole-word-masking')
テキストから単語ベクトルを作成
- Mecabで使う辞書を指定
- 形態素解析を行う
- set関数を使ってユニークな要素を得ることでこのデータセットのボキャブラリを取得
- 文字列からインデックス、インデックスから文字に治す辞書及び、配列を作成
with open('train.txt', 'r', encoding='utf-8') as f:
text = f.read().replace('\n', '')
mecab = MeCab.Tagger("-Owakati")
text = mecab.parse(text).split()
vocab = sorted(set(text))
char2idx = {u: i for i, u in enumerate(vocab)}
idx2char = np.array(vocab)
text_as_int = np.array([char2idx[c] for c in text])
訓練用のデータセットを作成
- 系列長を128に設定
- numpy配列からデータセットを作成
- データセットを系列長で分割 ※ターゲットが次の時刻の単語になるため、系列長+1のデータを利用する
seq_length = 128
# 訓練用サンプルとターゲットを作る
char_dataset = tf.data.Dataset.from_tensor_slices(text_as_int)
sequences = char_dataset.batch(seq_length+1, drop_remainder=True)
def split_input_target(chunk):
input_text = chunk[:-1]
target_text = chunk[1:]
return input_text, target_text
dataset = sequences.map(split_input_target)
文生成モデル
今回のデータセットのボキャブラリーにあった長さの出力になるようにbertにボキャブラリー数分のノードを持つ全結合層を付加したモデルを作成して転移学習を行う ※Inputの定義の際には、入力系列の長さが可変になるように引数shapeに(None,)を与える ※この訓練においてはBERTの重みは固定で全結合層部分のみを学習させるため、言語モデルの損失関数ではなく、単純にクラス分類のためのスパースクロスエントロピー誤差を用いる (one-hot表現でない整数ラベルに対して用いるクロスエントロピー誤差)
BATCH_SIZE = 64
BUFFER_SIZE = 10000
dataset = dataset.shuffle(BUFFER_SIZE).batch(BATCH_SIZE, drop_remainder=True)
input_ids = tf.keras.layers.Input(shape=(None, ), dtype='int32', name='input_ids')
inputs = [input_ids]
bert.trainable = False
x = bert(inputs)
out = x[0]
Y = tf.keras.layers.Dense(len(vocab))(out)
checkpoint_dir = './training_checkpoints'
checkpoint_prefix = os.path.join(checkpoint_dir, "ckpt_{epoch}")
checkpoint_callback=tf.keras.callbacks.ModelCheckpoint(
filepath=checkpoint_prefix,
save_weights_only=True)
model = tf.keras.Model(inputs=inputs, outputs=Y)
def loss(labels, logits):
return tf.keras.losses.sparse_categorical_crossentropy(labels, logits, from_logits=True)
model.compile(loss=loss,
optimizer=tf.keras.optimizers.Adam(1e-7))
model.fit(dataset,epochs=50, callbacks=[checkpoint_callback])
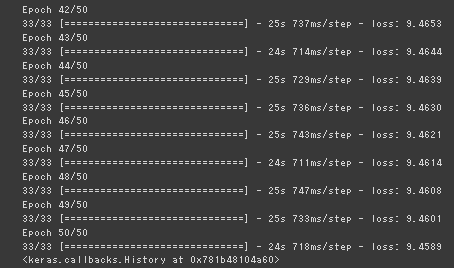 Loss関数の値は低下傾向のままなので、まだ学習が進む余地はあるが、GPU利用制限にかかってしまうので、途中で終了
Loss関数の値は低下傾向のままなので、まだ学習が進む余地はあるが、GPU利用制限にかかってしまうので、途中で終了

考察
上記のモデルで推論を実行した結果、学習が足りないのか、まだ自然な文章とはなっていない。
また、あくまでBERT部分は固定されていて、ボキャブラリが今回のデータセットに合うように射影しているだけなので、
元のデータセットのボキャブラリ(※32000)と今回のボキャブラリ(12750)の数が半分以下で違ったこと、元のデータセットがWikiから取ったデータで、今回のデータが夏目漱石の作品に限ったために、年代による文体の違いなどから、あまりうまく行かなかったのでは無いかと思われる。
 ※参考:cl-tohoku/bert-base-japanese-whole-word-masking · Hugging Face
※参考:cl-tohoku/bert-base-japanese-whole-word-masking · Hugging Face
文章のクラス分類
- テキストファイルを行単位で分割
- ターゲットを分類のone-hotベクトルとして定義
def input_target(chunk):
input_text = chunk
target = tf.constant([1, 0, 0], dtype=tf.float32)
return input_text, target
kokoro = tf.data.TextLineDataset('kokoro.txt')
kokoro = kokoro.map(input_target)
学習結果
 こちらもまだ精度は上がるが、GPU利用制限のため、50で中断
こちらもまだ精度は上がるが、GPU利用制限のため、50で中断
推論結果
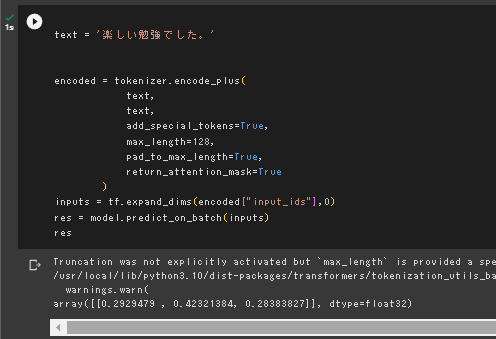 デフォルトのインプットの一文がどこにも見つからなかったので、
「それから」から固有名詞を含む1行を抜き出して再度実行
デフォルトのインプットの一文がどこにも見つからなかったので、
「それから」から固有名詞を含む1行を抜き出して再度実行
 期待としてはi=1の要素が一番高くなってほしかったが、こころに対応する要素が最も高くなってしまった。
学習が不十分な可能性がある。
期待としてはi=1の要素が一番高くなってほしかったが、こころに対応する要素が最も高くなってしまった。
学習が不十分な可能性がある。
4_8_interpretability.ipynb
CAM,Grad-CAM 共通で最後の畳み込みそうの出力が必要
- model.summary()などで、畳み込み層の名前を確認
- model.get_layer(確認した畳み込み層の名前).outputで畳み込み層の出力を得る
- 畳み込み層の出力に掛ける係数を算出する
- Grad-CAM の場合
- 勾配情報が必要なので、モデル定義時に勾配情報を保存するようにtf.GradientTape()のwithブロックで順伝播処理をくくる
- Grad-CAMの場合はtape.gradient(勾配の基準(クラス判定結果)、たどるところまで(畳み込み層の出力))で勾配を得る
- Global Average Pooling (tf.reduce_mean )
- ReLUを使う
- CAMの場合
- GAP→クラスの重みをmodel.get_layer (対象のレイヤー名).weightsで取得
- Grad-CAM の場合
実行結果
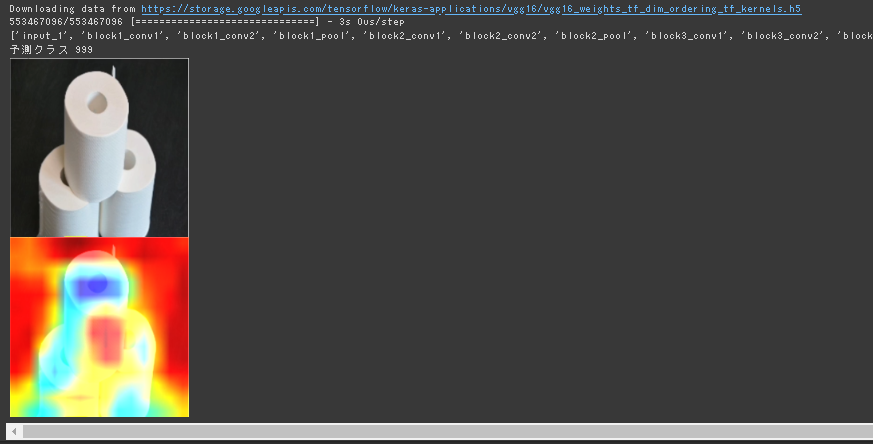 トイレットペーパーの穴の部分でトイレットペーパー判定している。
一応円柱部分も寄与していると思われる。
トイレットペーパーの穴の部分でトイレットペーパー判定している。
一応円柱部分も寄与していると思われる。
dcgan.ipynb
リソースの問題で実行できないが、認定テスト等で出された重要箇所についてまとめる。
Discriminatorの更新
real_lossとfake_lossがあるが、 バイナリクロスエントロピーを取るときに比較するラベルが、ことなることに注意
- real_loss : 値が全て1のベクトルと比較
- fake_loss : ゼロベクトルと比較
def update_discriminator(self, noize, real_data):
fake_data = self.G(noize)
with tf.GradientTape() as d_tape:
real_pred = self.D(real_data)
fake_pred = self.D(fake_data)
real_loss = tf.keras.losses.binary_crossentropy(
tf.ones_like(real_pred), real_pred
)
fake_loss = tf.keras.losses.binary_crossentropy(
tf.zeros_like(fake_pred), fake_pred
)
# batchの平均をとる
real_loss = tf.math.reduce_mean(real_loss)
fake_loss = tf.math.reduce_mean(fake_loss)
adv_loss = real_loss + fake_loss
d_grad = d_tape.gradient(adv_loss, sources=self.D.trainable_variables)
self.d_optimizer.apply_gradients(zip(d_grad, self.D.trainable_variables))
if self.make_logs:
with self.summary_writer.as_default():
tf.summary.scalar("d_loss", adv_loss)
self.summary_writer.flush()
return adv_loss