要点(最低100字)

機械学習モデリングプロセス

1. 問題設定
2. データ選定
3. 前処理
4. 機械学習モデル剪定
5. モデルの学習
6. モデルの評価

ルールベースと機械学習の比較

タスクTと性能指標Pがあるときに、性能が経験Eによって改善されるとき、 タスクTおよび性能指標Pに関して経験E から学習すると言われる

人がプログラムするのは学習の仕方　（認識の仕方では無い） ルールベースは認識の仕方自体をプログラムする。

主なモデル

• 教師あり学習
  • 回帰
    • 線形回帰・非線形回帰：最小二乗法、尤度最適化
  • 分類
    • ロジスティック回帰；尤度最大化
    • 最近傍・K-近傍アルゴリズム
    • SVM：マージン最大化
• 教師なし学習
  • クラスタリング
    • K-Means
  • 次元削減
    • 主成分分析：分散最大化

回帰問題

入力（説明変数、特徴量）から出力（目的変数）を予測する問題 一般的に、外挿問題（学習データに含まれない範囲の値域）での予測の精度が下がる。 どの学習方法でも共通。

線形回帰

線形とは→ざっくりというと比例。　n次元の超平面の方程式

直線、平面→線形回帰 曲線、局面→非線形

線形回帰に関連する値

• 教師データに含まれるもの
  • 入力$\vec{x} = (x_1,x_2,\dots,x_m)^\top \in R^m$
  • 出力$y\in R$
• 学習によって最適化していくもの
  • パラメータ$\vec{w} = (w_1,w_2,\dots,w_m)^\top \in R^m$$
  • 切片$w_0$
• 学習の際に使う値
  • 予測値$\hat{y} = w_0 + \sum_{i=1}^n \vec{w}^\top \vec{x}$　（※データセットで考えるときは$\vec{\hat{y}} = X・\vec{w}$）
  • 誤差$\epsilon = y - \hat{y}$

線形回帰の最適化手法(最尤法)

最小２乗誤差　$MSE = \frac{1}{n_{train}}\sum(y-\hat{y})^2$ を用いて最適化する。 $\hat{\vec{w}} = arg \min_{w \in R^m} MSE$ MSEが最小値を取るとき

$$\frac{\partial MSE}{\partial \vec{w}} = 0$$

$$\frac{\partial MSE}{\partial \vec{w}} = \frac{1}{n_{train}}\frac{\partial}{\partial \vec{w}}(X・\vec{w}-Y)^2$$

$$ = \frac{1}{n_{train}}\frac{\partial}{\partial \vec{w}}(X・\vec{w}-Y)^{\top}(X・\vec{w}-Y)$$

$$ = \frac{1}{n_{train}}\frac{\partial}{\partial \vec{w}}(\vec{w^{\top}}・X^\top-Y^\top)(X・\vec{w}-Y)$$

$$ = \frac{1}{n_{train}}\frac{\partial}{\partial \vec{w}}(\vec{w^{\top}}X^\top X\vec{w}　- \vec{w^{\top}}・X^\top Y - Y^\top X・\vec{w} + Y^\top Y)$$ 第２項と３項は$(AB)^T = B^T A^T$より同じ、 $\frac{\partial w^T X}{\partial w} = X$,$\frac{\partial w^T A x}{\partial w} = (A+A^T)w$, $(X^T X)^T = X^T X$から第１項は$2X^\top X\vec{w}$ $$=\frac{1}{n_{train}}(2X^\top X\vec{w} - 2X^\top Y) = 0$$

以上より、 $\hat{\vec{w}} = (X^T X)^{-1}X^T Y( = X^{-1}Y)$

学習後の予測値は

$$\hat{y} = w_0 + \sum_{i=1}^n \vec{\hat{w}}^\top \vec{x}$$

$$ = X_{test} (X_{train}^T X_{train})^{-1}X_{train}^T Y_{train}$$ ※逆行列は常に存在するわけでは無い、一般化逆行列をもちいる。

[!note] 外れ値に弱いという特徴があるので、Huber損失、Tukey損失を使うこともある

実装

最小構成

from sklearn.linear_model import LinearRegression

model = LinearRegression() #モデルインスタンスの生成
model.fit(input_train,target_train) # 学習

prediction = model.predict(input_test) # 予測結果


model.coef_ # 学習後に各特徴量の係数が得られる

model.intercept_ # 学習後の切片

非線形回帰

特徴量の２次以上の項を使ったり、非線形関数を使った回帰。

• 説明変数について非線形
• パラメータについては線形

$\Phi$は基底関数。 よく使われる基底関数として

• 多項式関数：$\phi_j = x^j$
• ガウス型基底関数：$\phi_j = exp(\frac{(x-\mu_j)^2}{2h_j})$ $where h_j = \frac{\sigma^2}{2}$
• スプライン関数/Bスプライン関数がある

非線形回帰に関連する値

• 教師データに含まれるもの
  • 入力$\vec{x} = (x_1,x_2,\dots,x_m)^\top \in R^m$ ※mは特徴量の数
  • 出力$y\in R$
• 学習によって最適化していくもの
  • パラメータ$\vec{w} = (w_1,w_2,\dots,w_k)^\top \in R^k$
  • 切片$w_0$
• 学習の際に使う値
  • 非線形関数ベクトル$\phi(\vec{x}) = (\phi_1(\vec{x}),\phi_2(\vec{x}),\dots,\phi_k(\vec{x}))^\top \in R^k$　※kは基底関数の数、基底関数はハイパーパラメータ
  • 予測値$\hat{y} = w_0 + \sum_{i=1}^n \vec{w}^\top \Phi(\vec{x})$　
  • 誤差$\epsilon = y - \hat{y}$

非線形回帰に関する最適化

非線形回帰となっているが、パラメータについては線形なので、結局計算式はほぼ変わらない。 差分は基底関数によって説明変数を一度別の空間に飛ばしているだけ。

学習後の予測値は線形回帰のときの説明変数の行列Xを$\Phi(X)$に入れ替えれば良いので、 $$\hat{y} = \Phi(X_{test}) (\Phi(X_{train})^T \Phi(X_{train}))^{-1}\Phi(X_{train})^T Y_{train}$$

分類問題

• 識別的アプローチ：入力Xが与えられたときのクラスｋに当てはまる確率自体をモデル化する
• 生成的アプローチ：事前確率と観測モデルをモデル化して、ベイズの定理を用いて事後確率を求める

回帰問題と違い目的変数の値域が狭いので、関数で射影して値域を狭める。 よく使うのは

ロジスティック回帰など分類問題で使われる。

値域は$[0,1]$ でx=0のとき0.5,

$\frac{1}{1+exp(-x)}$

微分値は　 $\frac{\delta\sigma(x)}{\delta x} = \sigma(x)\times (1-\sigma(x))$

ロジスティック回帰

確率的な出力をする分類器。 識別的アプローチになる。

目的変数 $P(Y=y_i|\vec{x_i}) = \sigma(\vec{w}^T\cdot\vec{x_i})^{y_i}\times(1-\sigma(\vec{w}^T\cdot\vec{x_i}))^{1-y_i}$

データからその分布のパラメータを推定したい。

尤度関数の最大化を行う。（このとき、同じ確率分布から得られた独立のデータ点という独立同分布の仮定を置く） L(w) = $\Pi_{i=0}^n (\sigma(\vec{w}^T\cdot\vec{x_i})^{y_i}\times(1-\sigma(\vec{w}^T\cdot\vec{x_i}))^{1-y_i})$

※シグモイド関数の影響で解析的に解くことが困難なため、勾配降下法によって求める

パラメータ最適化

勾配降下法を行う場合も損失関数をパラメータで微分した値を求めるのは同じ。 最適パラメータを求める方法がパラメータ更新という手法になる。

損失関数の微分値

尤度関数を最大化するにあたって、以下のように損失関数を定義する。

$E(w) = -log(L(w))$と置くと。　※logは単調増加関数なので、尤度関数最大のとき損失関数最小

$E(w) = -\sum_{i=1}^n(y_i\cdot log(p_i) + (1-y_i)log(1-p_i))$ $E(w) = \sum_{i=1}^n E_i(w)$,$z_i = w^Tx_i$とすると

$$\frac{\partial E(w)}{\partial w} = \sum_{i=1}^n\frac{\partial E_i(w)}{\partial p_i} \times \frac{\partial p_i}{\partial z_i} \times \frac{\partial z_i}{\partial w}$$ 　 $$\frac{\partial E(w)}{\partial w} = \sum_{i=1}^n(-1)(\frac{y_i}{p_i}-\frac{1-y_i}{1-p_i})\times(p_i \cdot (1-p_i))\times(x_i)$$

$$\frac{\partial E(w)}{\partial w} = \sum_{i=1}^n(-1)(y_i-p_i)\times(x_i)$$

勾配降下法

学習率$\eta$と損失関数の微分値を用いて以下のようにパラメータを更新する。

$$w^{(k+1)} = w^{(k)} - \eta \frac{\partial E(w)}{\partial w} = w^{(k)} + \eta \sum_{i=1}^n(y_i-p_i)x_i$$

※　すべてのデータを用いるので、メモリや計算時間が大きい問題がある。 →　確率的勾配降下法

確率的勾配降下法

ランダムにデータを一個選んで、それによってパラメータを更新する。 勾配降下法で１回更新する間に、データ数回分パラメータを更新できるので効率が良い。

$$w^{(k+1)} = w^{(k)} - \eta \frac{\partial E_i(w)}{\partial w} = w^{(k)} + \eta (y_i-p_i)x_i$$

SVMサポートベクターマシン

決定的な出力を出す分類器。

線形SVM：$y(x) = w^Tx + b$ 非線形SVM：$y(x) = w^T\Phi(x) + b$

マージンを最大化する境界面を与えるパラメータw,bを学習する。 予測は$sign{y(x)}$で正例負例を分類。 ソフトマージン：誤分類を許容する割合を調整する係数Cと誤分類のとき１，それ以外を０とするスラック変数の積の和を評価関数に追加し、汎化性能を高める。C→∞で誤分類を許容しない。C→０で誤分類に寛容になる。 カーネル法：決定境界を新しい空間に転写し、線形にすることで線形問題として解くことが可能になる カーネルトリック：関数が級数展開できることから内積計算を一つの関数による射影で計算簡略化する

カーネル変数$k(x,x\prime) = \Phi(x)^T\cdot \Phi(x)$ $\Phi(x)$は特徴ベクトル

マージン：決定境界面と最も近いデータとの距離 サポートベクトル：境界面と最も近いデータ点。マージン上の点

k近傍法

最近傍のデータをk個取って来てそれらが最も多く所属するクラスに識別する。 kは比較するデータ点数の数 怠惰学習に属し、データ暗記するだけなので、 訓練フェーズは明には存在せず、データや特徴量が多くても訓練は高速に終わる。 一方で予測に関してはデータ点との距離の比較が必要になるので、データ点や特徴量が多いと時間がかかる 決定境界は線形とは限らない

kを大きくすると境界線（決定境界）がなめらかになる→ノイズがあるデータではｋを大きくすると良い ｋが大きいと精度が上がるわけでは無いので、ハイパーパラメータとして調整が必要。 kは訓練時間、予測時間にあまり影響を与えない。

未学習と過学習

• 未学習　Underfitting　学習データに対して十分小さな誤差が得られないモデル
  • 原因　モデルの表現力不足
  • 対策　表現力の高いモデルの利用　次数を上げるなど。
• 過学習　Overfitting
  • 原因　表現力が高すぎる　（データサンプル不足もあるが、その場合はデータを増やす）
  • 対策　表現力の抑制
    • 不要な基底関数の削除
    • 損失関数に正則化項(罰則項)を追加することで表現力を抑制する

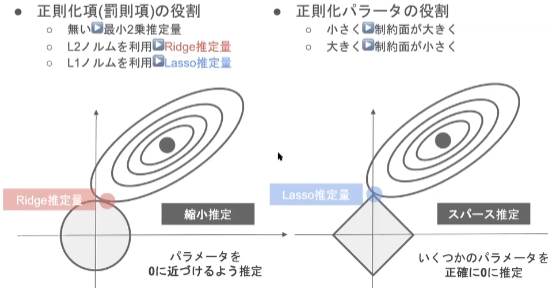
正則化のビジュアル的なイメージ

正則化項　$R(\vec{w})\leq \gamma$の条件を満たす損失関数$E(\vec{w})$の最小値を与えるパラメータ$\vec{w}$は $E(\vec{w})$の等高線と$R(\vec{w})= \gamma$でで描かれる図形の接点となる。 座標空間はパラメータ$\vec{w}$と同次元。

L１ノルムを使った正則化をすると、頂点で接点を持つ確率が高いので、余分なパラメータを０にする効果がある。 L2ノルムを使った正則化をすると、パラメータ全体の値がちいさくなる効果がある

<講義動画より引用>

教師なし学習

次元削減

主成分分析　（PCA：Principal conponent analysis）

データの分散が最大になるような空間に射影する。もとの変量、説明変数を合成してデータをうまく説明する主成分を生成する。 射影の結果変数統合された潜在変数の意味の解釈は主観的になり、一意に定まらないことに注意。 主成分はノルムが１になるように正規化し、主成分同士は直行するように設定する

1. もとの座標系で各軸ごとの平均値を引く
2. $\vec{PC} = argmax_{\vec{PC}} \sum_i^N {\vec{x_i} \cdot \vec{PC}}^2$ （$|\vec{PC}| = 1$）

再構成誤差：主成分に射影したあと元の空間に戻したときにどれだけ誤差が出るか。データが一直線上にある時には最高性誤差は0%

メモ

• 主成分の数の最大は特徴量の数
• 非線形変換は出来ない
• どれだけの主成分を残すべきかは、Total Varianceに対して、Variance by PCがどのくらいあるかで判断する。可視化の観点では3次元以下

# Make the bar plot

plt.bar(np.arange(num_factor_exposures), pca.explained_variance_ratio_);

画像圧縮に使われることもある 主成分分析による画像圧縮

クラスタリング

• 階層型と非階層型のアルゴリズムがある
  • 階層型のクラスタリング構造はデンドログラムと言われる
• いくつのグループに分けるかは選択可能
• 用いる類似度は様々な定義の仕方がある

K-Means

ｋはクラスタの数

1. 各クラスタの中心の初期値を設定
2. 各データ点に対して、各クラスタ中心との距離を計算して最も近いクラスタに割り当て
3. クラスタの中心を更新
4. 収束するまで２，３を繰り返す

工夫

• クラスタの初期値やｋの値などを変えて複数回評価して、良い結果が得られたモデルを採用する
  • ｋは少なすぎても多すぎても良くない
  • クラスタがうまく離れるように初期値を与える

モデルの評価

誤差の収束と過学習、未学習

訓練誤差と検証誤差を比較することで判断する。 ￥

• 未学習：訓練誤差と検証誤差ともに大きい
• ちょうど良い：訓練誤差と検証誤差ともに小さい
• 過学習：訓練誤差は小さいが、検証誤差が大きい

データの分割

ホールドアウト法

単純な方法。

学習用とテスト用の２つに分割して、 予測精度や誤り率などの指標を算出するのに利用。

• データ分割の割合で学習性能と評価性能のトレードオフが発生する
• データが大量にある場合を除いて性能が出にくい

クロスバリデーション法　CV法

データを分割したあと、イテレーションごとに学習用とテスト用の役割を変えながら繰り返す。 このイテレーションごとに得られる性能値の平均をCV値という

実装演習結果

線形回帰モデル（ボストンの不動産価格予測）

• 説明変数
  • CRIM： 町ごとの一人当たり犯罪率
  • ZN ：25,000sq.ft.以上の住宅用地に指定された土地の割合
  • INDUS：町ごとの非小売業用地面積の割合
  • CHAS ：チャールズ川のダミー変数（川に面している場合は1、そうでない場合は0）。
  • NOX ：一酸化窒素濃度（1,000万分の1)
  • RM ：一戸あたりの平均部屋数
  • AGE ：1940年以前に建てられた持ち家の割合
  • DIS：ボストンの5つの雇用中心地までの距離の加重平均
  • RAD ：放射状高速道路へのアクセス指数
  • TAX ：1万ドルあたりの固定資産税評価額
  • PTRATIO： 町ごとの生徒と教師の比率
  • B ：1000(Bk - 0.63)^2 ただし、Bkは町ごとの黒人の割合である。
  • LSTAT： 下層階級の人口割合
• 目的変数
  • MEDV　1000ドル単位の持ち家の中央値

個人的に一から実装したコード

# -*- coding: utf-8 -*-

"""housing_price_regression.ipynb

Automatically generated by Colaboratory.

Original file is located at
    https://colab.research.google.com/drive/1pjg8KYQ3yZfN420k_deyI_pvOnMG4Rvb
"""

from sklearn.datasets import load_boston
from pandas import DataFrame
import numpy as np
from sklearn.linear_model import LinearRegression

#前処理用
from scipy.stats import zscore
from sklearn.preprocessing import MinMaxScaler

#可視化用
import matplotlib.pyplot as plt

# データセットの取得

boston = load_boston()
df = DataFrame(boston['data'],columns=boston['feature_names'])
df['target']=boston.target


# 前処理なしで学習


## 学習用変数をデータセットから抽出


target_train = df.loc[:,'target'].values
input_train = df.loc[:,boston['feature_names']].values

## モデルの学習


model = LinearRegression()
model.fit(input_train,target_train)

## 学習結果の可視化　各特徴量の寄与度を確認（後のデータ前処理ありとの比較用）

plt.bar(boston['feature_names'],list(model.coef_))
plt.show()

# 前処理ありで学習


## 学習用変数をデータセットから抽出


mm = MinMaxScaler()
standardized_target_train = mm.fit_transform(df.loc[:,'target'].values.reshape(-1,1)).squeeze()
standardized_input_train = df.loc[:,boston['feature_names']].apply(zscore).values

## モデルの学習


model_2 = LinearRegression()
model_2.fit(standardized_input_train,standardized_target_train)

## 学習結果の可視化　各特徴量の寄与度を確認

plt.bar(boston['feature_names'],list(model_2.coef_))
plt.show()

## TOP3とBOTTOM3の取得と可視化

sorted_indices_by_coef = np.argsort(model_2.coef_)
top3_positive_features = boston['feature_names'][sorted_indices_by_coef[:-4:-1]]
worst3_negative_features = boston['feature_names'][sorted_indices_by_coef[:3]]


print('Top 3 Positive Features\n')

for i,feature in enumerate(top3_positive_features):
  print(f'{i+1}:{feature}')
#endfor

print('\nWorst 3 Negative Features\n')
for i,feature in enumerate(worst3_negative_features):
  print(f'{i+1}:{feature}')
#endfor

出力の画像

＜標準化なしで各特徴量の係数の可視化を行った結果＞

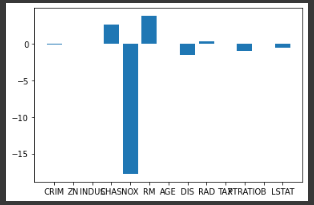
＜説明変数を標準化,目的変数を正規化して各特徴量の可視化を行った結果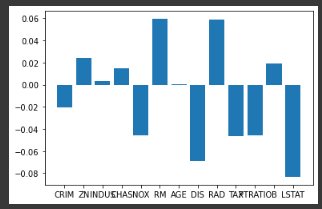＞ ＜TOPとBOTTOMの特徴量３つ＞

課題（部屋数が4で犯罪率が0.3の物件はいくらになるか？）

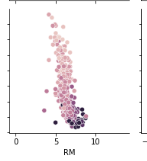
部屋数と犯罪率を説明変数、住宅価格を目的変数として重回帰分析を行い、 指定のパラメータを与えて推論を行った。 結果は約4,240ドル 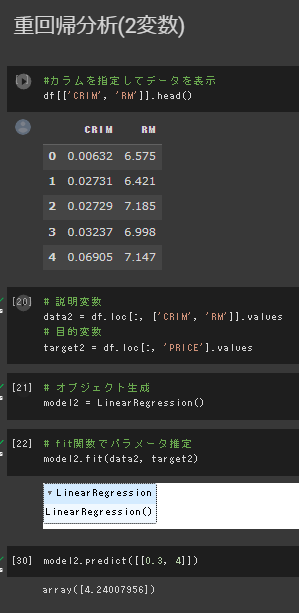わかりづらいが、下図を見るとRMのデータが5-10の範囲に偏っているため、その範囲外は外挿による推定となり、精度が下がる可能性がある。

実装演習、モデルの評価

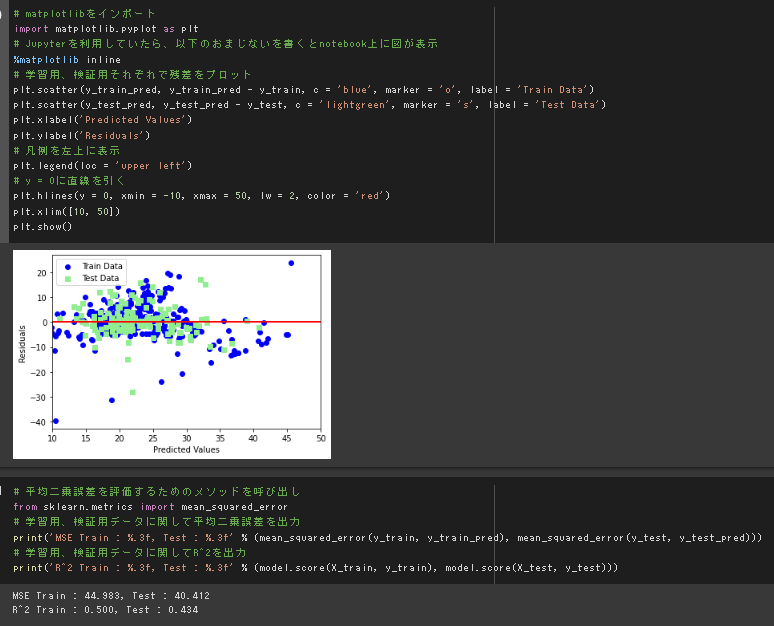訓練データとテストデータの誤差の平均や分布を見るに、過学習は指定なさそうだと思われる。 一方で、決定係数からモデルの当てはまりの良さはあまり良くはない(<0.5)ので、いくつかの工夫が必要な様に見受けられる。

非線形回帰モデル（四次式にノイズを加えた目的関数を推定）

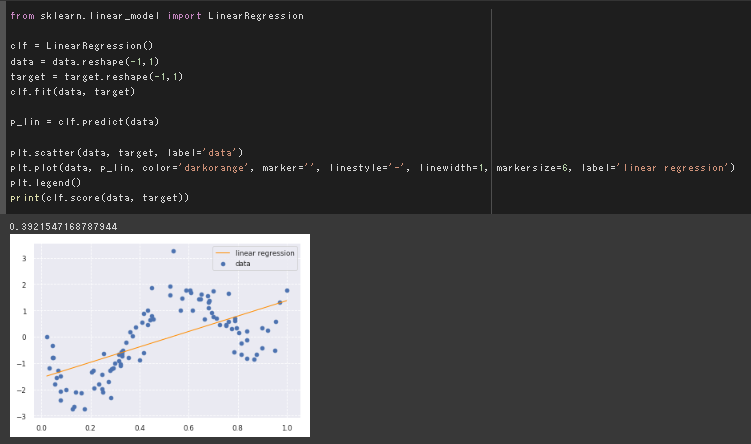
線形回帰

ベースラインとして線形回帰を最初に行った。 当たり前だが、モデルの表現力が足りていない。

RBFカーネルを用いた非線形回帰

デフォルトの実行結果

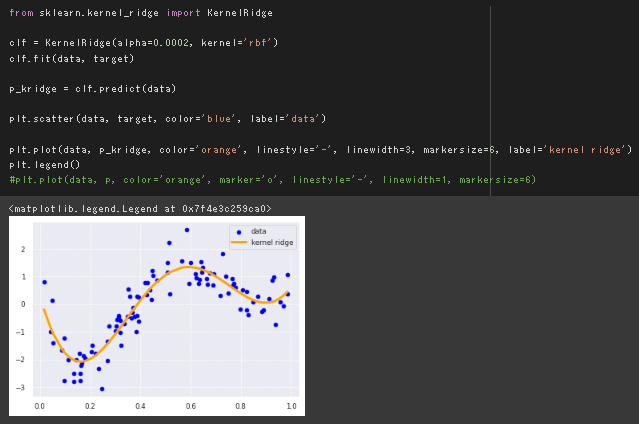
rbfカーネル関数とRidge回帰を組み合わせた実装

リッジ回帰とRBFカーネルのパラメータを変更してみる。 デフォルトのalpha=0.0002,γ=1/n_featuresで同じ結果が得られることを確認。

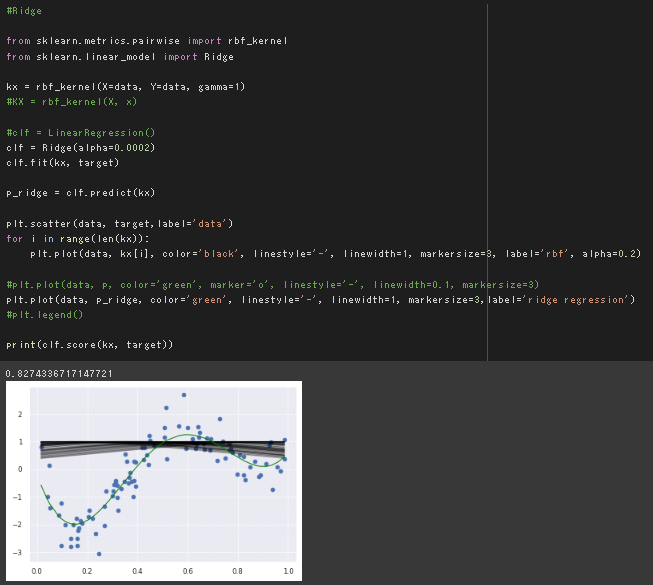
罰則項の係数を上げる

alpha=0.02 (１００倍)で確かに表現力が落ちていることを確認

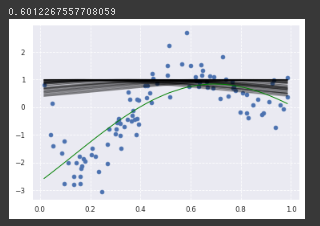
RBFカーネルのγを変更

γ＝１００（１００倍）にすると一つひとつのデータへの感度が上がることを確認。 RBFカーネルが$K(x, x’)=\exp(-\gamma||x-x’||^2)$で表されることを考えると妥当な結果。

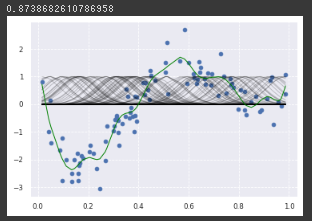
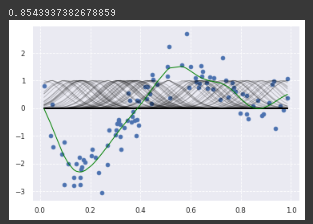
RBFカーネルと罰則項のパラメータを変更

alpha=1 (5000倍),γ＝１００（１００倍） 罰則項の係数を大きくすることである程度、過学習は抑制できたが、RBFカーネルのパラメータ設定が間違っていると不自然な傾向が見られる。 非線形変換を行う部分に対応するので、 RBFカーネルのパラメータ設定は規定の1/n_featuresを参考にして、 極端な値にしないことが望ましいのではないかと感じた。

多項式回帰

PipeLineを用いて、複数処理を一つのモデルに追加。

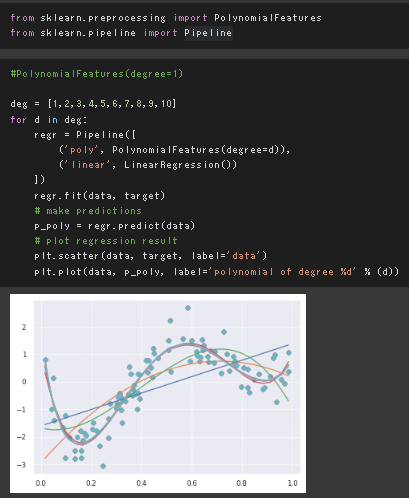
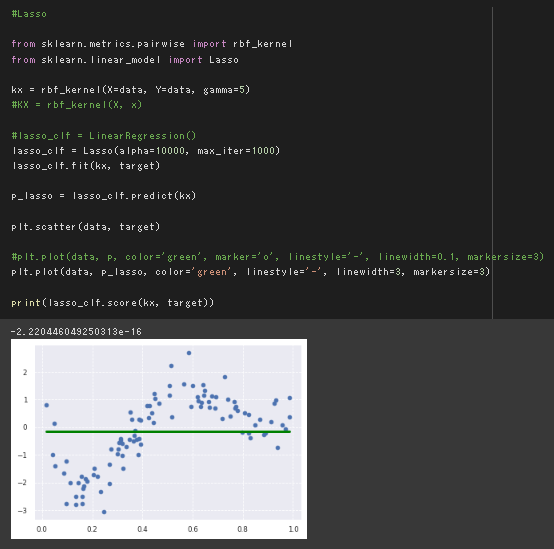
ラッソ回帰

スパース化を行うラッソ回帰で罰則化項を極端にした結果。 モデルの表現力を抑制しすぎた結果、平均値を出力するだけのモデルとなった。

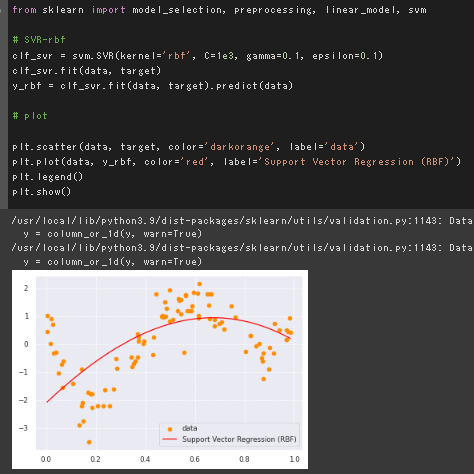
SVR

Cは誤差への感度、イプシロンは誤差を無視する範囲を調整する。 ハイパーパラメータの調整はグリッドサーチでCV後の決定係数の良い組み合わせを採用する。

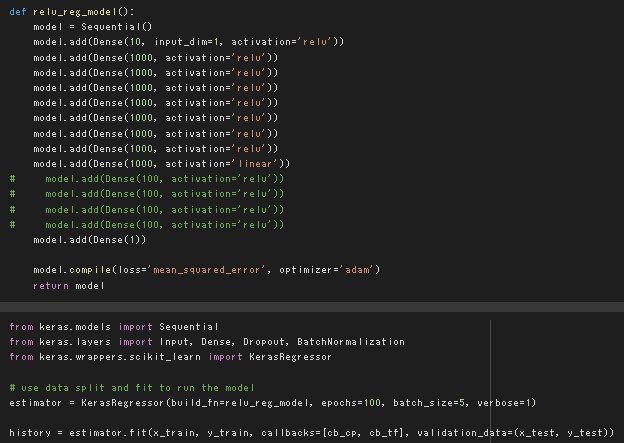
単純な全結合のDeepLearningモデルによる非線形回帰

デフォルトの設定ではかなり層数が多いのと、パラメータ数もデータ点数に対して過剰に見受けられるが、結果的にはある程度うまく行っている。

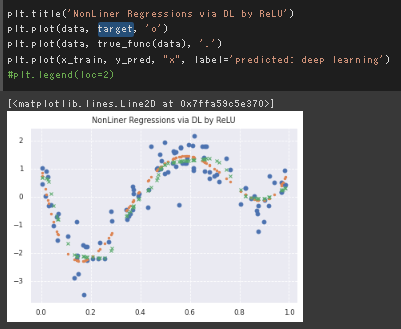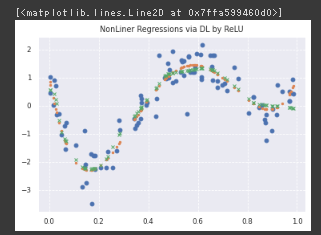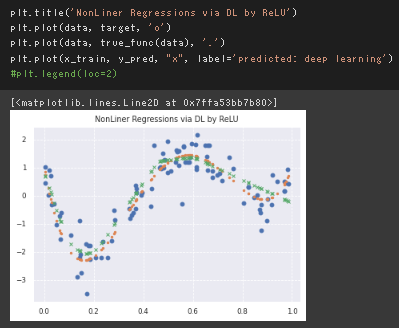
今回のケースではせいぜい４次の多項式なので、４層前後で良いのではないかと考えて実行したところ、四層でも十分な表現力が得られた。 また、今回のケースはDLを使用しているもののほぼ古典的な範囲なので、パラメータ数はサンプル数のオーダーで十分と想定して調整したところ、おおよそ問題なかった。 （データ点数が９０だったので、隠れ層１:10,隠れ層2:30,隠れ層3:30,隠れ層4:30のパラメータを当てた） もとの設定だと明らかに過剰な表現力を持っていたが、過学習していないのは近年話題になっていたOverparametrized Regimeに関連する二重降下の影響と想定。

ロジスティック回帰モデル（タイタニックの生存者の予測）

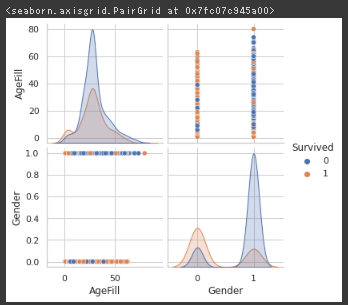
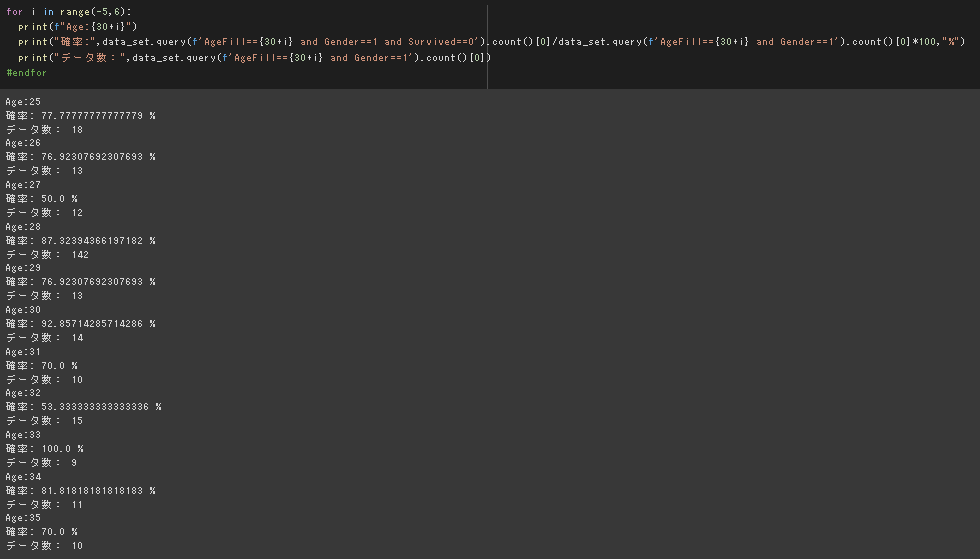
課題：年齢が３０歳で男の乗客は生き残れるか？

８割がた死亡するという結果。 元データの分布を見ても妥当な結果だと思われる。

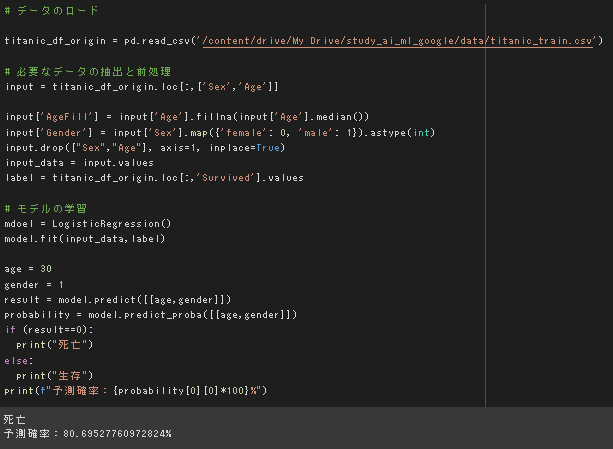
個人的に１から実装したコード

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import zscore
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegressionCV
from sklearn.metrics import accuracy_score,recall_score,precision_score,f1_score
%matplotlib inline

# kaggle公式から落としてきたデータのロード

titanic_df = pd.read_csv("./datasets/titanic/train.csv")
test_titanic_df = pd.read_csv("./datasets/titanic/test.csv")


# 欠損値の確認

for column in titanic_df.columns:
    print(f"Does {column} have null record? : {'yes' if any(titanic_df[column].isna()) else 'No'}")
#endfor

for column in test_titanic_df.columns:
    print(f"Does {column} have null record? : {'yes' if any(test_titanic_df[column].isna()) else 'No'}")
#endfor

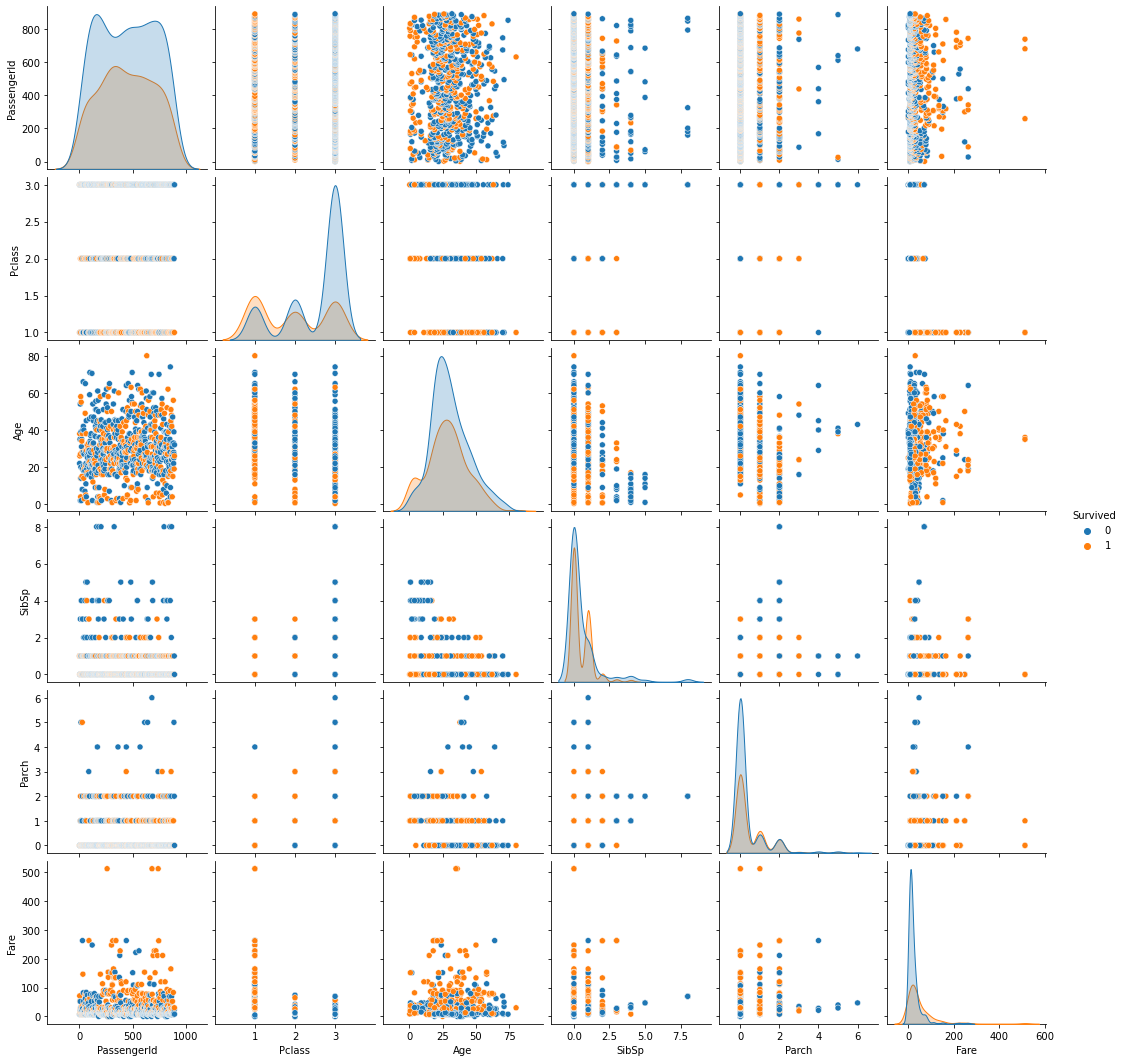
# データの確認

sns.pairplot(titanic_df,hue='Survived')
plt.show()


# [markdown]

# Passenger IDは特に意味のあるデータでは無いので、対象から外す。

# 名前は家族関係などを示すため意味が無いとは言えないが、数値変換するのが今回に関して困難なため削除。

# チケット番号はIDのようなもののため削除。

# キャビン番号は活動位置情報に関わりそうだが、今回は見送り。やるならアルファベッド部分ごとに列をつくって続く数字を変数とするか？

# Survivedが目的変数で0=死亡,1＝生存

# 順序尺度は線形変換＋シグモイドでそのまま解釈がうまく行かなさそうなのと、分布的にone-hotベクトルに変更したほうがうまく行きそうなので、２パターン作って確認する



# 前処理用の関数定義


## one-hot coding

def one_hot(df,columns):
    for column in columns:
        for symbol in df[column].unique():
            if not (str(symbol)=='nan'):
                df[column+'_'+str(symbol)] = (df[column]==symbol).apply(int)
        #endfor
    #endfor

## 前処理　名義尺度の変数をone-hotコーディングするのと、余分なカラムの削除、スケーリングを行う

def preprocess_titanic_df(df,standard_scalar,is_train=True):
    """
    df:                 DataFrame (titanic dataset)
    standard_scalar:    StandardScalar Instance, use same instance for train and test dataset. 
    is_train:           bool
    """
    output_df = df.copy()
    # change numerical value


    one_hot(output_df,['Sex','Embarked'])
    # remove unnecessary columns


    output_df.drop(['PassengerId','Name','Ticket','Cabin','Sex','Embarked'],axis=1,inplace=True)
    # manage missing data


    output_df.loc[output_df['Age'].isna(),'Age'] = output_df['Age'].mean()
    output_df.loc[output_df['Fare'].isna(),'Fare'] = output_df['Fare'].mean()
    # change scale


    ## regularize variables on ratio scale


    if is_train:
        output_df['Age','Fare','SibSp','Parch'](https://half-broken-engineer.github.io/'Age','Fare','SibSp','Parch') = standard_scalar.fit_transform(output_df['Age','Fare','SibSp','Parch'](https://half-broken-engineer.github.io/'Age','Fare','SibSp','Parch'))
    else:
        output_df['Age','Fare','SibSp','Parch'](https://half-broken-engineer.github.io/'Age','Fare','SibSp','Parch') = standard_scalar.transform(output_df['Age','Fare','SibSp','Parch'](https://half-broken-engineer.github.io/'Age','Fare','SibSp','Parch'))
    #endif
    ## normalize variable on ordinal scale 

    PCLASS_MAX = 3
    PCLASS_MIN = 1
    output_df['Pclass'] = (output_df['Pclass'] - PCLASS_MIN)/(PCLASS_MAX-PCLASS_MIN)
    return output_df

## 順序尺度の方も変更one-hotベクトルに変更

def preprocess_titanic_df_2(df,standard_scalar,is_train=True):
    """
    df:                 DataFrame (titanic dataset)
    standard_scalar:    StandardScalar Instance, use same instance for train and test dataset. 
    is_train:           bool
    """
    output_df = df.copy()
    # change numerical value


    one_hot(output_df,['Sex','Embarked','Pclass'])
    # remove unnecessary columns


    output_df.drop(['Pclass','PassengerId','Name','Ticket','Cabin','Sex','Embarked'],axis=1,inplace=True)
    # manage missing data


    output_df.loc[output_df['Age'].isna(),'Age'] = output_df['Age'].mean()
    output_df.loc[output_df['Fare'].isna(),'Fare'] = output_df['Fare'].mean()
    # change scale


    ## regularize variables on ratio scale


    if is_train:
        output_df['Age','Fare','SibSp','Parch'](https://half-broken-engineer.github.io/'Age','Fare','SibSp','Parch') = standard_scalar.fit_transform(output_df['Age','Fare','SibSp','Parch'](https://half-broken-engineer.github.io/'Age','Fare','SibSp','Parch'))
    else:
        output_df['Age','Fare','SibSp','Parch'](https://half-broken-engineer.github.io/'Age','Fare','SibSp','Parch') = standard_scalar.transform(output_df['Age','Fare','SibSp','Parch'](https://half-broken-engineer.github.io/'Age','Fare','SibSp','Parch'))
    #endif
    return output_df

#前処理
std_scaler = StandardScaler()
titanic_df_preprocessed = preprocess_titanic_df(titanic_df,std_scaler)
test_titanic_df_preprocessed = preprocess_titanic_df(test_titanic_df,std_scaler,is_train=False)
std_scaler_2 = StandardScaler()
titanic_df_preprocessed_2 = preprocess_titanic_df_2(titanic_df,std_scaler_2)
test_titanic_df_preprocessed_2 = preprocess_titanic_df_2(test_titanic_df,std_scaler_2,is_train=False)
titanic_df_preprocessed_2.head()

# 学習器にかけるデータの準備

feature_train = titanic_df_preprocessed[titanic_df_preprocessed.columns[1:]].values
feature_train_2 = titanic_df_preprocessed_2[titanic_df_preprocessed_2.columns[1:]].values
label_train = titanic_df_preprocessed["Survived"].values
feature_test = test_titanic_df_preprocessed[titanic_df_preprocessed.columns[1:]].values
feature_test_2 = test_titanic_df_preprocessed_2[titanic_df_preprocessed_2.columns[1:]].values

# ロジスティック回帰モデルの学習

logi_reg = LogisticRegressionCV()
logi_reg2 = LogisticRegressionCV()
logi_reg.fit(feature_train,label_train)
logi_reg2.fit(feature_train_2,label_train)

# 予測

train_prediction = logi_reg.predict(feature_train)
test_prediction = logi_reg.predict(feature_test)

train_prediction_2 = logi_reg2.predict(feature_train_2)
test_prediction_2 = logi_reg2.predict(feature_test_2)

<各特徴量と生存者の分布の確認>

主成分分析（乳がん検査データ）

デフォルトの実行結果

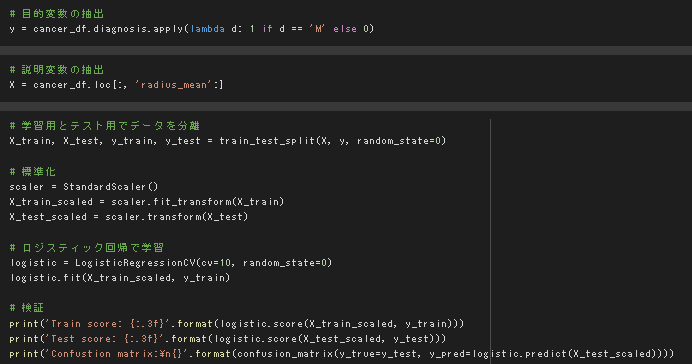
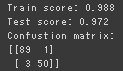極端な正例と不例の偏りはなく、訓練とテストの精度がともに高いのでうまく予測できている様に思われる。

32次元のデータを2次元上に次元圧縮した際に、うまく判別できるかを確認

主成分分析と主成分ごとの寄与率の確認

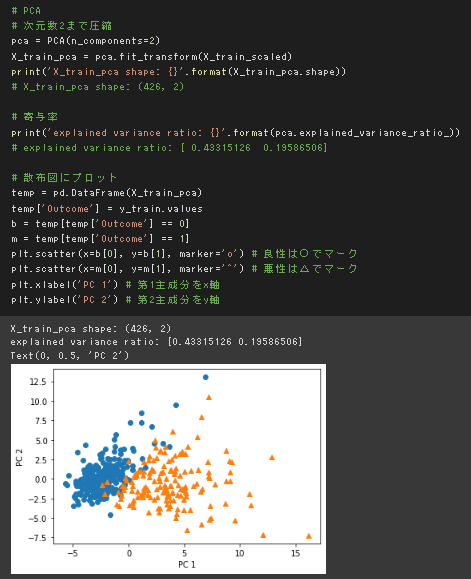
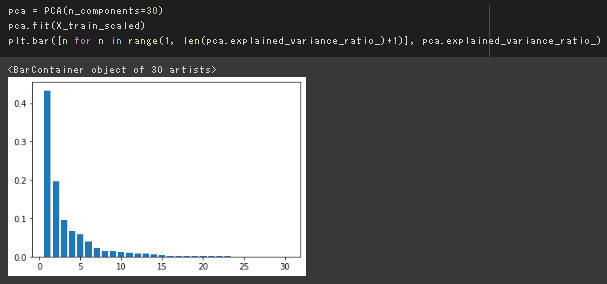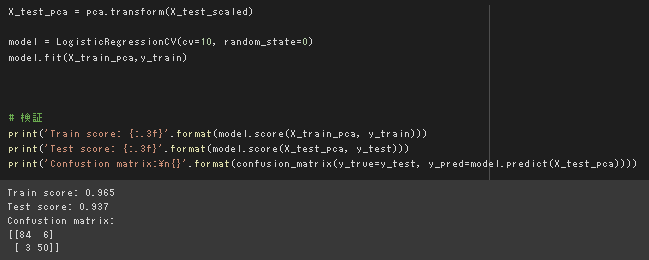
下図から第２主成分までの累積寄与率は６割強であることがわかる。 第二主成分までを使った２次元プロットでデータの分布を確認した。 分布を見たところ、境界付近での難しさはありそうだが、境界線は引ける様に見受けられる。 上記のPCAモデルを用いて写像変換したデータでロジスティック回帰を行った。 テストデータの精度は若干下がったものの９割を超えており、うまく判別できていると言える。

K-Means

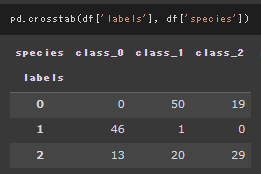
デフォルト設定、各クラスタ中心の初期値をk-means++で実行した場合。 k-means++は完全なランダムではなく、一つのクラスタ中心をランダムに設定したあとはそこから離れた点が選ばれる確率を上げてクラスタ中心の初期値を設定する。 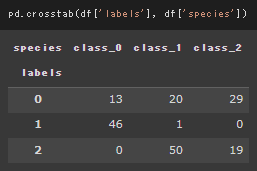初期値を完全ランダムにした場合。 ラベルとクラス間の対応が若干変わっているが、本質的な結果に変わりはなかった。 以上のことから、ここから精度を上げるにはクラスタ中心の初期設定ではなく、特徴量エンジニアリングやモデルの変更が必要だとわかる。

サポートベクターマシン（該当ファイルなし、非線形回帰のところでSVRを実装演習した）

考察

ボストン不動産価格予測

運用上の気づき

説明変数の標準化を行っておかないと各特徴量の影響度が比較しづらくなるので、 モデル学習の前の前処理も適切に行う必要がある。 今回は目的変数が住宅価格のメジアンということで、外れ値影響が少ないと考えられることから、 目的変数については価格がマイナスになると分かりづらいと考えて正規化にしたが、 説明変数に前処理を入れていれば特徴量間の比較という目的が果たせるので、説明変数については人から見たときに値の大小がわかりやすい元の値のままにしておくのが望ましいのでは無いかと考えた。

結果に対して

演習結果に載せたように、 プラス影響のTOP３は

1. 一戸あたりの平均部屋数
2. 放射状高速道路へのアクセス指数
3. 25,000sq.ft.以上の住宅用地に指定された土地の割合

マイナス影響を与えるWorst３は

1. 下層階級の人口割合
2. ボストンの5つの雇用中心地までの距離の加重平均
3. 1万ドルあたりの固定資産税評価額

となっている。 基本的には特徴量が住環境やコストにかかわるため、特徴量→目的変数の因果が明確になっていそうだが、 Worstの特徴量の下層階級の人口割合については、周辺住民の質という観点で近い要素になりそうな犯罪率CRIMが相対的に寄与度が小さいことから、価格と特徴量の因果の方向についてさらなる確認が必要だと考える。 また、B（＝1000×(Bk -0.63)^2）の特徴量が２乗の値を取ってしまっているので、もとのBkの値によっては解釈を考える必要がある。

課題において設定されたパラメータがデータセット内であまり見られない値であったが、実際の分析においてもモデルを学習する際に使用したデータの分布と予測するさいに用いるデータの分布の違いについては把握しておく必要があると感じた。

タイタニックの生存者の予測

はじめの特徴量の整理が重要に感じた。 特徴量が質的変数の場合はダミー変数生成の際に各カテゴリに対応した0,1のダミー変数をそれぞれ作成しないと行けないと考える。 ２クラスのときは一つのダミー変数でも良いが、欠損値を考えると、２つの特徴量に分割したほうが、表現しやすいと思われる。 データ量とのトレードオフと考えられるため、今回は元データを確認して、欠損値があるもののみ対応した。

欠損値があったものは、Age,Fare,Cabin,Embarked

• Pclass：順序尺度　→　one-hot coding
• Sex：名義尺度　→　one-hot coding
• Age：比例尺度　→　標準化、欠損値は平均値で補完
• SibSp：比例尺度　→　標準化
• Parch：比例尺度　→　標準化
• Fare：比例尺度　→　標準化、欠損値は平均値で補完
• Embarked：名義尺度　→　one-hot coding 欠損値は各クラスのダミー変数をすべて０にして対応

参考文献

https://www.math.uwaterloo.ca/~hwolkowi/matrixcookbook.pdf

Vimeoで 機械学習

サポートベクター回帰(Support Vector Regression, SVR)～サンプル数10000以下ならこれを使うべし！～ | データ化学工学研究室(金子研究室)＠明治大学 理工学部 応用化学科

https://cometscome.github.io/DLAP2020/slides/DL_Physics2020_mori.pdf